Introduction
Linear equations are fundamental in algebra and help solve real-life problems where relationships between two variables are involved. In Class 10 CBSE, the Pair of Linear Equations in Two Variables chapter explores how to represent and solve two linear equations simultaneously. This knowledge is essential for building algebraic skills and solving practical problems.
A linear equation in two variables is an equation of the form:
where ,
, and
are real numbers, and
and
are the variables. When we have two such equations, we call them a pair of linear equations in two variables.
For example, in the equations:
both involve the variables and
and represent a pair of linear equations in two variables.
Real-life Example
Akhila went to a fair in her village. She wanted to enjoy rides on the Giant Wheel and play a game called Hoopla. In Hoopla, you throw a ring at items in a stall, and if the ring fully covers any item, you win it.
In this situation:
- The number of times Akhila played Hoopla was half the number of rides she had on the Giant Wheel.
- Each ride on the Giant Wheel cost her ₹3.
- Each game of Hoopla cost her ₹4.
Akhila spent a total of ₹20 on these activities. Given this information, can we determine:
- The number of rides she took on the Giant Wheel.
- The number of times she played Hoopla.
To answer these questions, we need to translate this information into mathematical equations.
Formulating Equations
Let:
be the number of rides Akhila took on the Giant Wheel.
be the number of times she played Hoopla.
Based on the information provided, we can form the following equations:
- Since the number of times she played Hoopla is half the number of rides she took, we have:
- The total cost for the rides and games is ₹20. Given that each ride costs ₹3 and each game of Hoopla costs ₹4, we can write:
Now, we have a pair of linear equations:
Our goal is to find values of and
that satisfy both equations simultaneously. There are several methods to solve pairs of linear equations, which we will explore in the Graphical Method of Solution of a Pair of Linear Equations and Algebraic Methods of Solving a Pair of Linear Equations.
Graphical Representation of Linear Equations
Each linear equation in two variables represents a straight line when plotted on a graph. The graphical solution to a pair of linear equations is the point where the two lines intersect, representing the values of and
that satisfy both equations.
Types of Solutions
- Unique Solution: The lines intersect at a single point. This means the pair of equations has one unique solution.
- No Solution: The lines are parallel and do not intersect, meaning the equations are inconsistent and have no solution.
- Infinite Solutions: The lines coincide, meaning there are infinitely many solutions.
Methods for Solving Pair of Linear Equations
- Substitution Method: In this method, solve one equation for one variable and substitute it into the other equation.
Example: Solveand
by substitution.
- From the first equation,
.
- Substitute
in the second equation and solve for
.
- From the first equation,
- Elimination Method: In this approach, eliminate one variable by adding or subtracting the equations, then solve for the remaining variable.
Example: Solveand
by elimination.
- Multiply equations if necessary to make the coefficients of one variable equal, then add or subtract to eliminate it.
- Cross-Multiplication Method: This formula-based approach directly gives the values of
and
, and is particularly useful when other methods are too complex.
For equations of the form:
The values ofand
are given by:
Real-life Applications of Linear Equations
Linear equations in two variables are not just theoretical; they have real-world applications in fields like economics, business, physics, and everyday problem-solving. Some examples include:
- Budgeting: Determining spending on two different items while staying within a budget.
- Mixture Problems: Mixing solutions or products in specific ratios to achieve desired concentrations or qualities.
Distance and Speed: Calculating time, distance, or speed when dealing with two different moving objects.
Related Topics
- The Fundamental Theorem of Arithmetic
- Pythagoras Theorem
- Differentiation Formulas
- Maths FAQs
- Ordinal Numbers
- Congruence of Triangles
- Relationship between Zeroes and Coefficients of a Polynomial
- Probability
- Percentage
- Revisiting Irrational Numbers
- Rational Numbers
- Real Numbers
- Mensuration
- Roman Numerals
- Area of Triangle



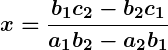







Get Social