Introduction to Resistance
Resistance is a property of a conductor that opposes the flow of electric current through it. The greater the resistance, the more difficult it is for charges to flow through the conductor. This opposition is caused by collisions between the moving electrons and the atoms of the material, which slows down the flow of current.
The SI unit of resistance is the ohm (), named after Georg Simon Ohm. One ohm is defined as the resistance that allows a current of one ampere to flow through a conductor when a potential difference of one volt is applied across it.
In this section, we will explore the various factors that affect the resistance of a conductor.
Factors Affecting the Resistance of a Conductor
The resistance () of a conductor depends on several factors, which can be summarized as follows:
- Length of the Conductor –
- Cross-sectional Area of the Conductor-
- Material of the Conductor –
– Resistivity
- Temperature of the Conductor
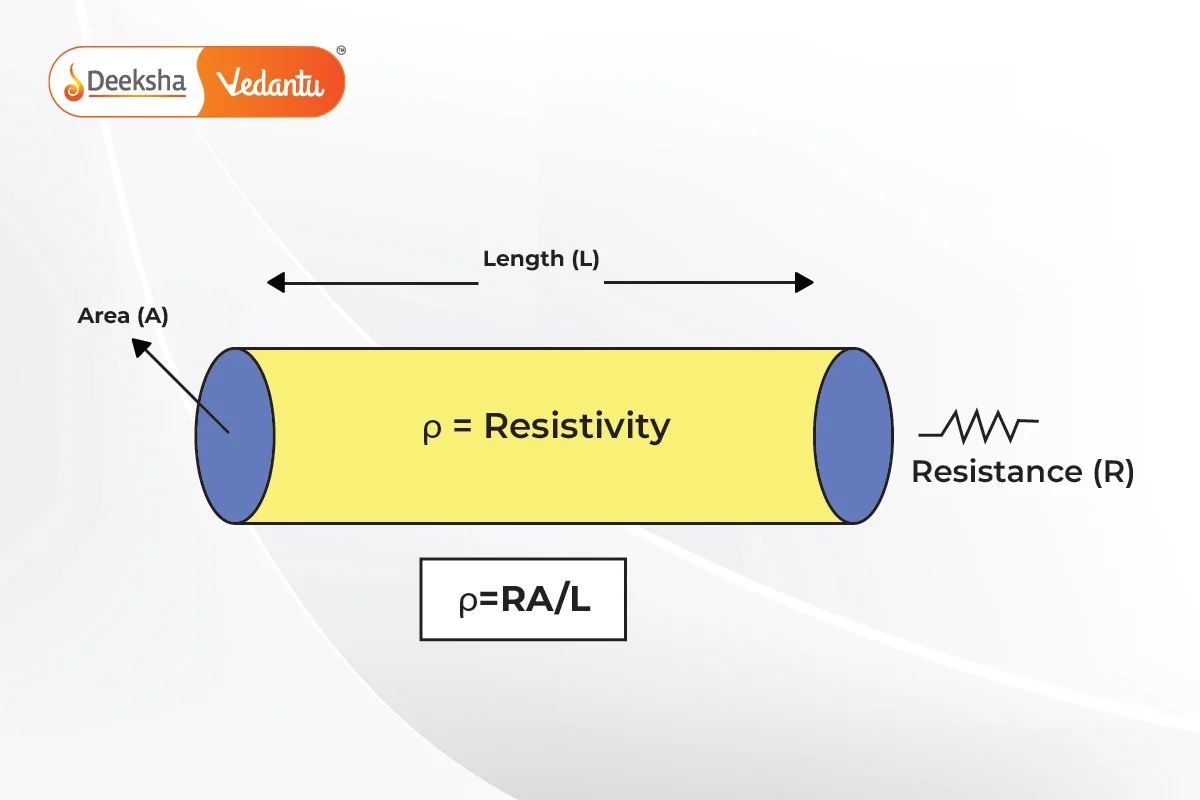
Length of the Conductor (l)
The length of the conductor has a direct relationship with its resistance. The longer the conductor, the more resistance it offers to the flow of electric current. This is because a longer conductor provides more collisions between the moving electrons and the atoms of the material, thus increasing the opposition to the current.
- Resistance io the length of the conductor:
- If the length of a conductor is doubled, its resistance will also double.
Example:
- A copper wire with a length of
has a resistance of
. If the length of the wire is increased to
, its resistance will increase to
.
Cross-sectional Area of the Conductor (A)
The cross-sectional area of the conductor is inversely proportional to its resistance. A conductor with a larger cross-sectional area offers less resistance to the flow of current because there is more space for the electrons to move through. A smaller cross-sectional area restricts the flow of electrons, resulting in higher resistance.
- Resistance is inversely proportional to the cross-sectional area of the conductor:
- If the cross-sectional area is doubled, the resistance will be halved.
Example:
- A wire with a cross-sectional area of
has a resistance of
. If the cross-sectional area is increased to
, the resistance will decrease to
.
Material of the Conductor – Resistivity (ρ)
The material of the conductor plays a significant role in determining its resistance. Different materials have different abilities to conduct electric current, which is quantified by a property called resistivity ().
- Resistivity is a material-specific property that measures how strongly a material opposes the flow of electric current.
- Conductors like copper and aluminum have low resistivity and therefore offer low resistance to current.
- Insulators like rubber and glass have high resistivity and offer high resistance to current.
- Relationship: Resistance is directly proportional to the resistivity of the material:
- Materials with higher resistivity will have higher resistance, even if their length and cross-sectional area are the same as materials with lower resistivity.
Example:
- Copper has a lower resistivity compared to iron, so a copper wire will have less resistance than an iron wire of the same length and cross-sectional area.
Table of Resistivity for Common Materials:
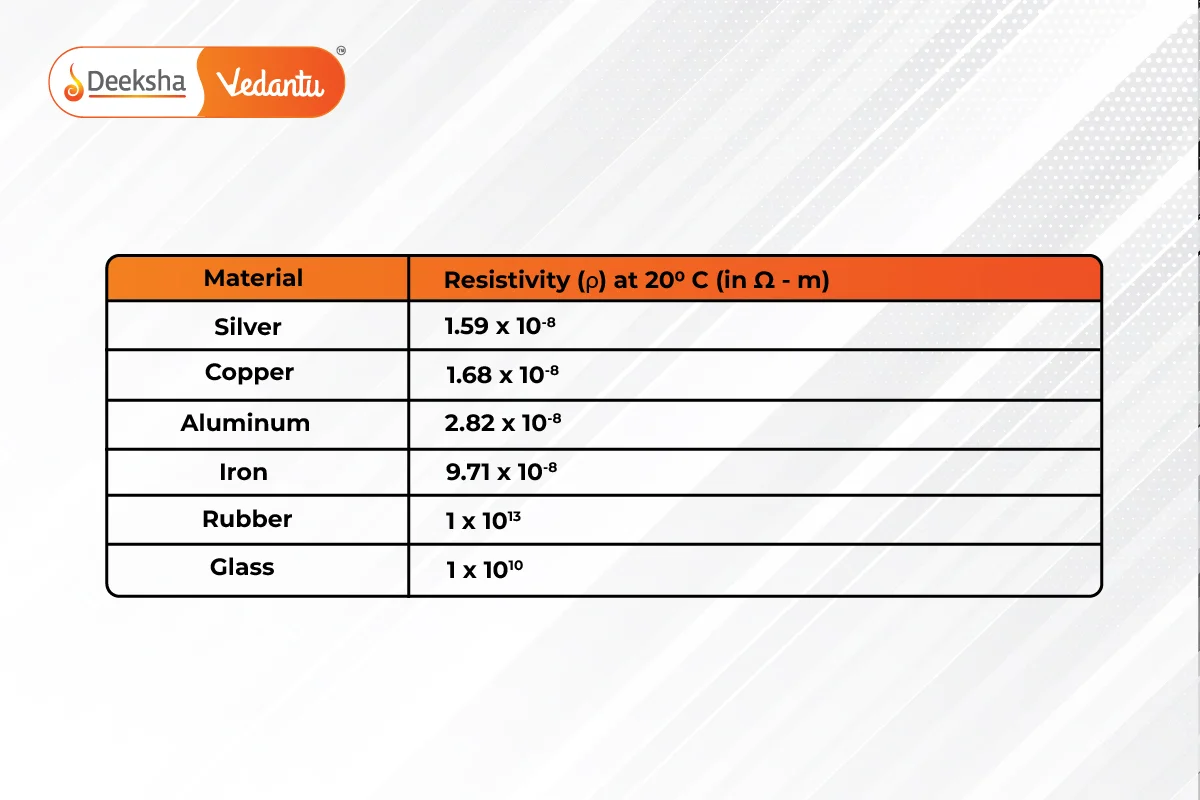
| Material | Resistivity |
| Silver | |
| Copper | |
| Aluminum | |
| Iron | |
| Rubber | |
| Glass |
Temperature of the Conductor
The temperature of the conductor also affects its resistance. In general, the resistance of most materials (especially metals) increases with an increase in temperature. This happens because, as the temperature rises, the atoms in the material vibrate more vigorously, causing more frequent collisions between the electrons and the atoms, which results in higher resistance.
- For metals, resistance increases with temperature.
- For some semiconductors, resistance decreases with temperature, as the number of free charge carriers increases at higher temperatures.
Example:
- The resistance of a copper wire increases when it is heated. For instance, a copper wire at room temperature (around
) might have a resistance of
, but at
, its resistance may increase to
.
Combining All Factors: The Formula for Resistance
The factors affecting the resistance of a conductor can be combined into a single formula, which is known as the resistance formula. The formula for the resistance of a conductor is:
Where:
This formula shows that resistance increases with the length of the conductor and the resistivity of the material and decreases with the cross-sectional area.
Practical Applications of Resistance
The concept of resistance is widely used in everyday life and technology. Understanding the factors that affect resistance helps in designing electrical circuits and components for various applications.
Electrical Wiring: Electrical wires are made from materials like copper and aluminum, which have low resistivity to minimize resistance and reduce energy losses in the form of heat. Wires are designed to have a certain cross-sectional area and length to optimize performance for different electrical loads.
Heating Appliances: Heating elements in appliances like electric heaters, toasters, and irons are made from materials with high resistance, such as nichrome. The high resistance generates heat when current flows through the element, providing the required heating effect.
Electronic Components: Resistors are fundamental components in electronic circuits, controlling the flow of current and voltage in devices like televisions, radios, and computers. These resistors are designed with specific resistances based on their material, length, and cross-sectional area.
Key Practice Questions
Q1: A wire has a resistance of and a length of 2 meters. If the wire is stretched to 4 meters while maintaining the same cross-sectional area, what will be its new resistance?
- Answer: The resistance is directly proportional to the length of the wire. So, if the length is doubled, the resistance will also double:
Q2: A wire has a resistance of and a cross-sectional area of
. What will be the resistance if the cross-sectional area is reduced to
, assuming the length and material remain the same?
- Answer: The resistance is inversely proportional to the cross-sectional area. If the area is halved, the resistance will double:
.
Q3: A copper wire has a length of 1 m and a cross-sectional area of . If the resistivity of copper is
, calculate the resistance of the wire.
- Answer:
The resistance of the copper wire is .
FAQs
Resistivity is a material-specific property that measures how strongly a material opposes the flow of electric current. The resistance of a conductor is directly proportional to its resistivity. Materials with low resistivity (like copper) have lower resistance, while materials with high resistivity (like rubber) have higher resistance.
For most conductors (such as metals), resistance increases with an increase in temperature due to more frequent collisions between electrons and atoms. However, some materials, like semiconductors, may exhibit decreased resistance with increasing temperature.
A thicker wire has a larger cross-sectional area, which provides more space for the flow of electric current, reducing the resistance. Resistance is inversely proportional to the cross-sectional area.
The resistance of a conductor is directly proportional to its length. If the length of the conductor increases, the resistance increases.












Get Social