Introduction to Young’s Double Slit Experiment
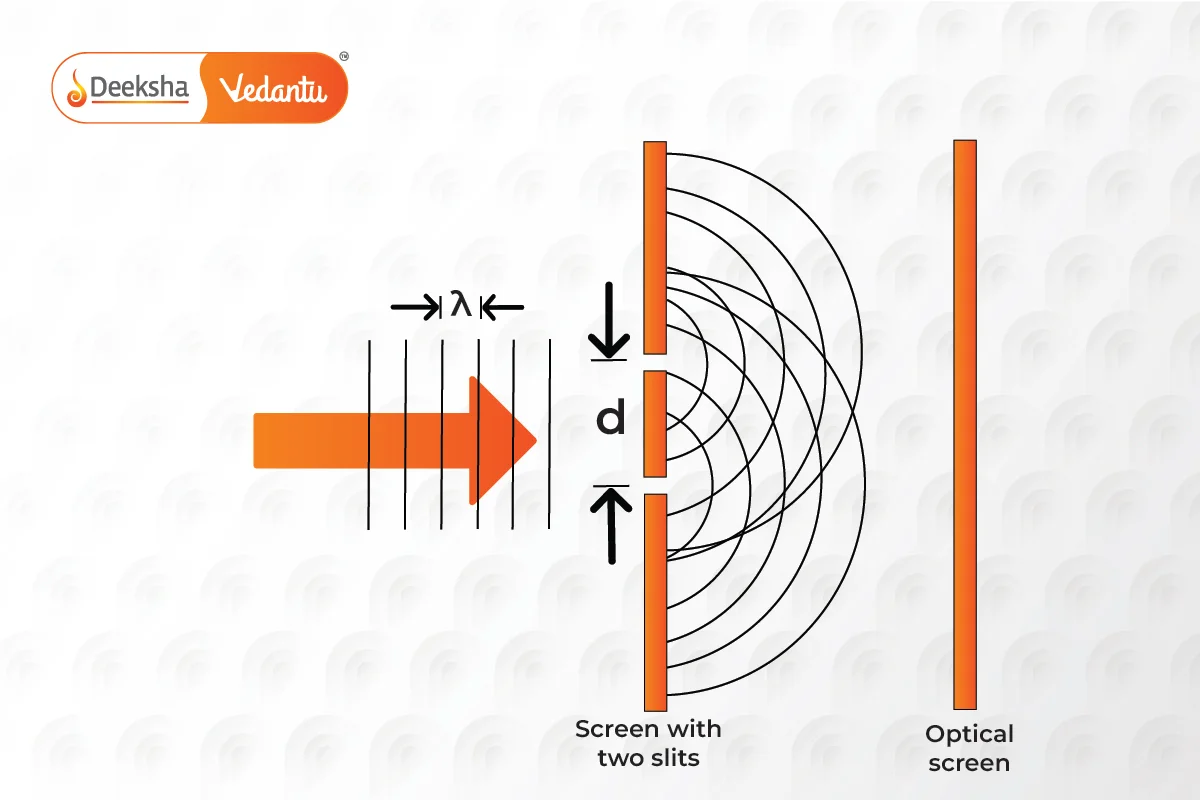

Young’s double slit experiment involves using two coherent light sources placed close together. The experiment demonstrates the wave nature of light by creating an interference pattern, essential for understanding wave theory. In modern experiments, lasers often replace the original light sources used by Young.
Experiment Setup
In the setup, light from a single source is diffracted through two slits, acting as coherent sources. A screen is placed at a distance from the slits to observe the interference pattern. The distance between the slits,
, is typically much larger than the wavelength of the light used.
Path Difference and Interference
Each slit acts as a coherent light source, and the light waves travel different paths to a point on the screen, creating a path difference . This path difference leads to constructive or destructive interference, forming bright and dark fringes on the screen.
Derivation and Fringes Formation
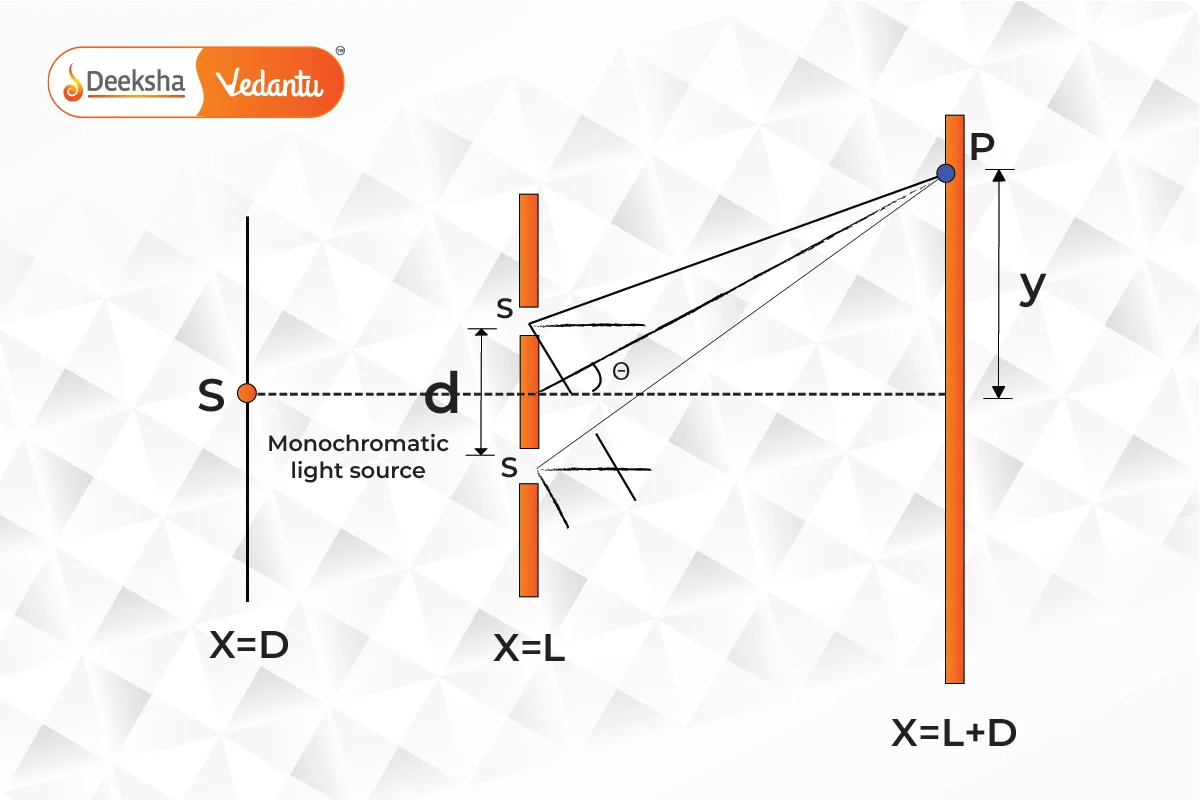
- Path Difference Calculation:
- For constructive interference (bright fringes):
- For destructive interference (dark fringes):
- For constructive interference (bright fringes):
- Position of Fringes:
- Bright fringes are located at:
- Dark fringes are located at:
Fringe Width
The distance between two consecutive bright or dark fringes is called the fringe width, denoted by :
When the setup is immersed in a medium with refractive index , the wavelength and fringe width reduce by a factor of
.
Angular Width
The angular width of the fringes is given by:
Maximum Order of Interference Fringes
The highest order of interference fringes is determined by:
Shape of Interference Fringes
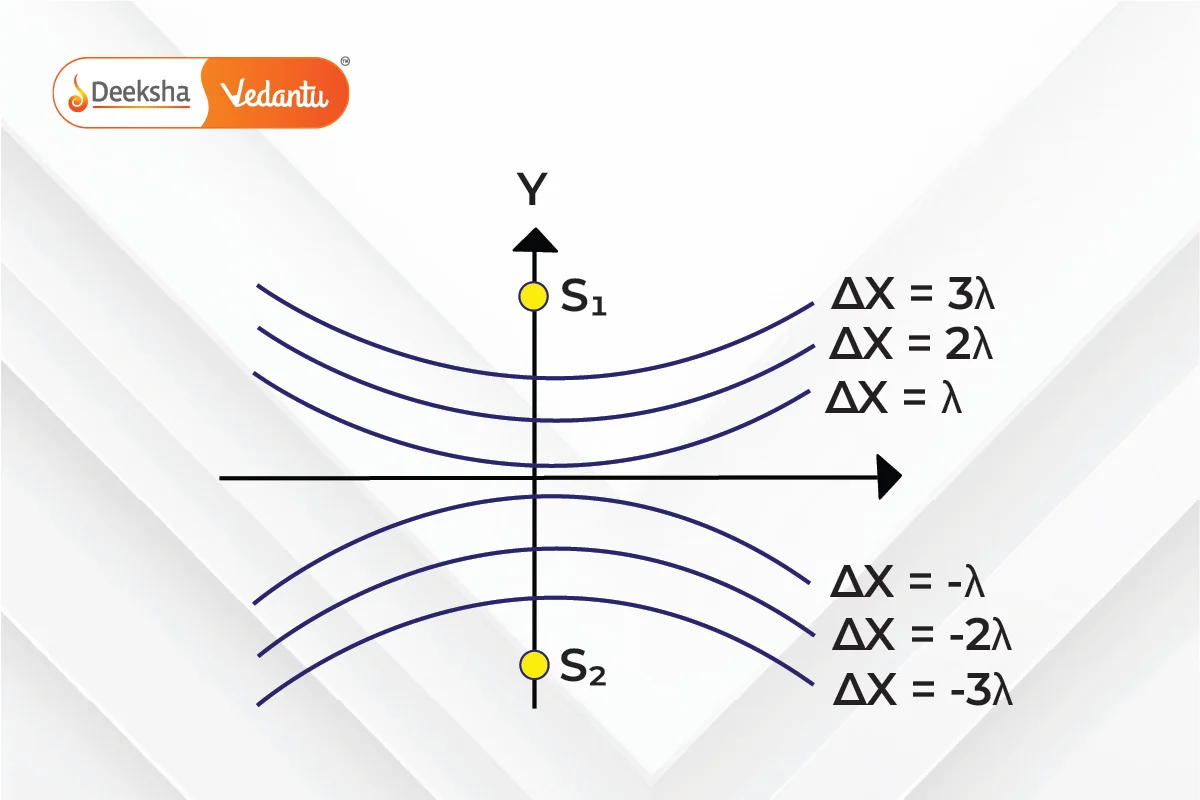
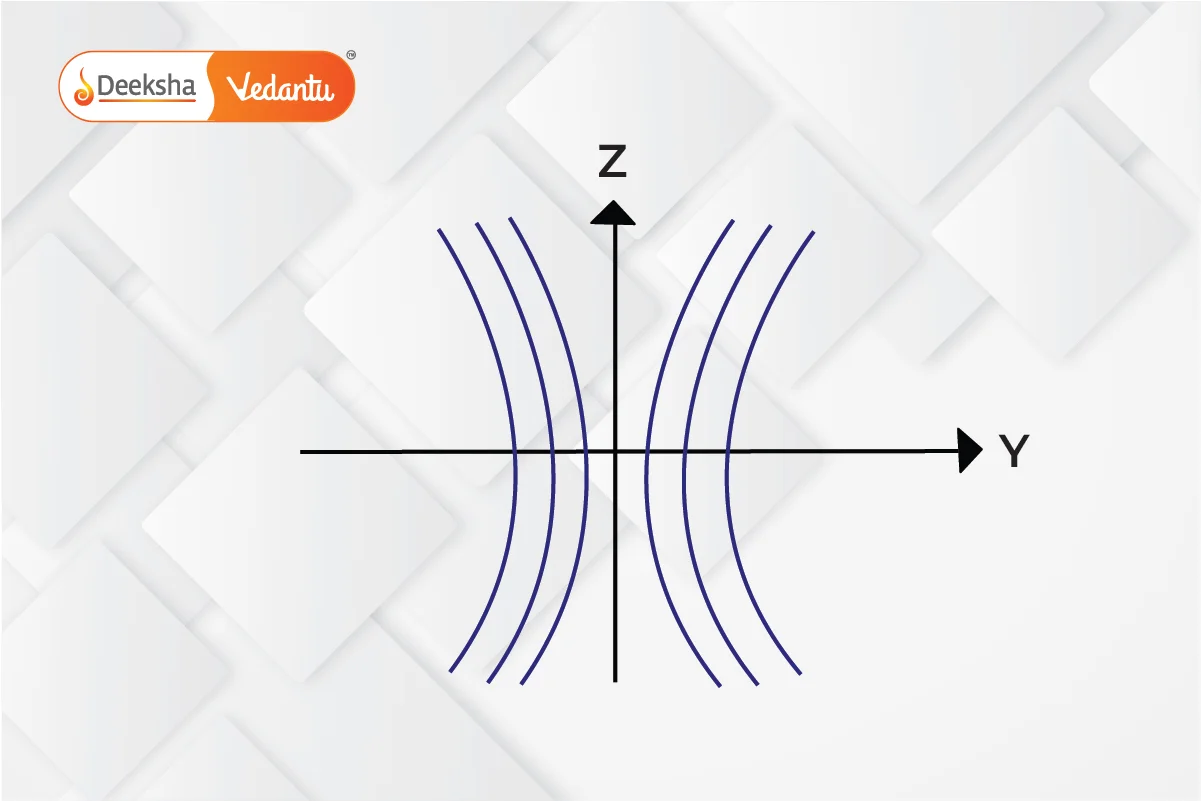
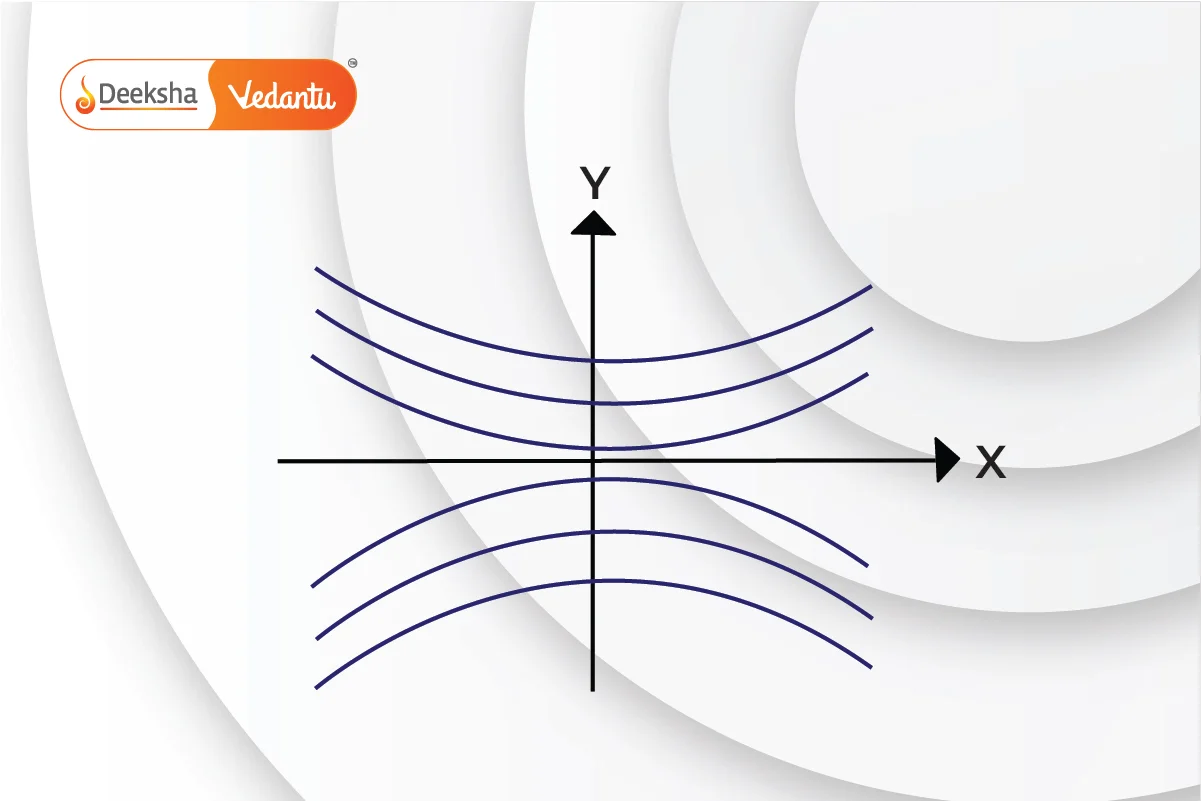
The interference fringes form hyperbolic patterns on the screen, with the central fringe being a straight line.
Intensity of Fringes
- The intensity of the fringes varies based on the phase difference
between the waves:
- For constructive interference:
- For destructive interference:
Special Cases and Practical Applications
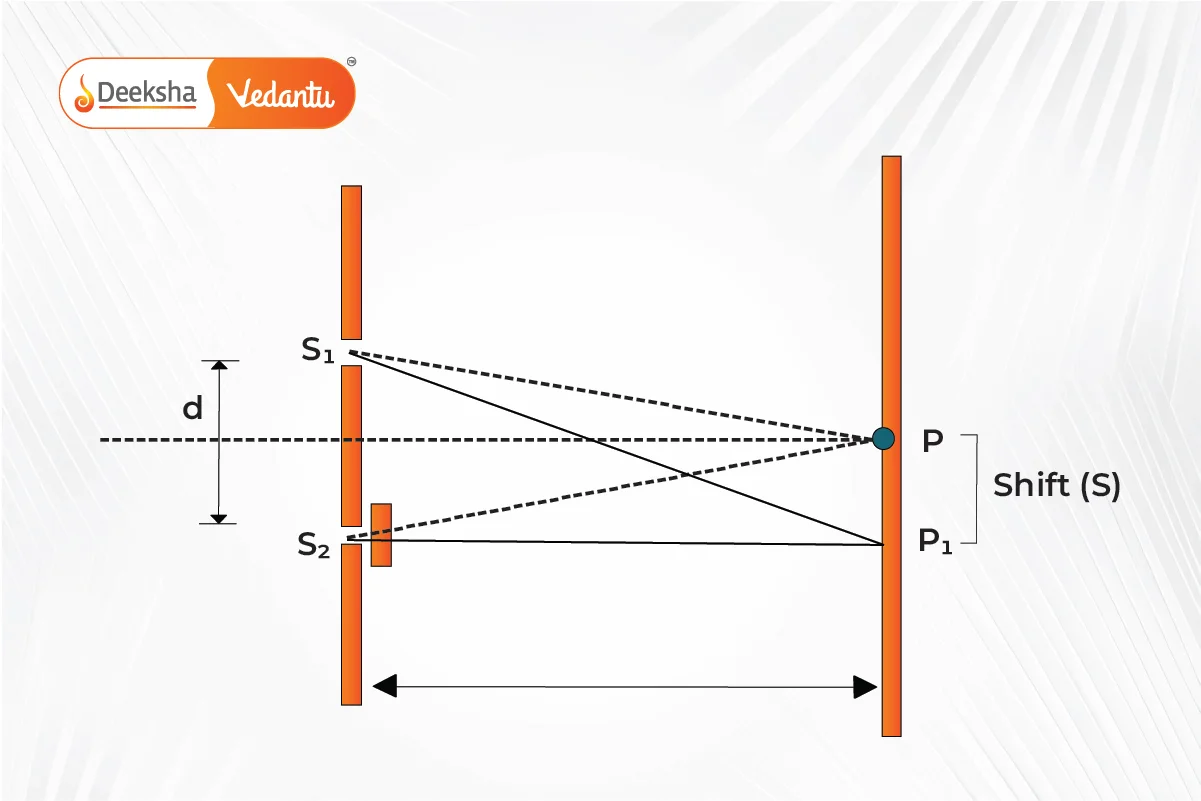
- Non-parallel Rays: Adjustments are made for non-parallel rays to calculate maxima and minima positions.
- Source Displacement: Shifts in fringe positions occur when the light source is displaced from the central line.
- Introduction of a Transparent Plate: Inserting a transparent plate causes a shift in the fringe pattern towards the plate.
Constructive and Destructive Interference
- Constructive interference occurs when the path difference is an integral multiple of the wavelength:
- Destructive interference occurs when the path difference is an odd multiple of half the wavelength:
Significance of Young’s Double Slit Experiment
This experiment confirmed the wave nature of light and influenced the understanding of matter, as similar interference patterns were later observed with electrons, suggesting that matter also exhibits wave-like properties.
FAQs
The wavelength of light determines the spacing of the fringes. Different wavelengths result in different fringe spacings, affecting the overall interference pattern.
Constructive interference occurs when the path difference is an integer multiple of the wavelength, resulting in bright fringes. Destructive interference occurs when the path difference is an odd multiple of half the wavelength, resulting in dark fringes.
The introduction of a transparent plate causes a shift in the fringe pattern towards the side with the plate, altering the path difference.
Fringe width is calculated using the formula , where
is the wavelength,
is the distance to the screen, and d is the separation between the slits.
The experiment demonstrated the wave nature of light, showing that light can exhibit interference patterns, a characteristic of waves.










Get Social