Understanding Heisenberg's Uncertainty Principle in Quantum Mechanics

Introduction

Heisenberg’s Uncertainty Principle is a foundational concept in quantum mechanics that describes the limits of precision for simultaneously measuring two complementary properties of particles, such as position and momentum. This principle highlights the intrinsic limitations of our ability to measure without disturbing a quantum system.

Understanding the Basics

Werner Heisenberg, a German physicist, introduced the Uncertainty Principle in 1927. It fundamentally challenges the classical mechanics notion of a particle having precise, simultaneous values for position and momentum. The principle is crucial for understanding the behavior of particles at microscopic scales, particularly in the realm of atoms and subatomic particles.

Mathematical Framework

The principle is commonly expressed through the inequality:

$\boldsymbol{\Delta x \Delta p \geq \frac{\hbar}{2}}$

Where:

$\boldsymbol{\Delta x}$ represents the uncertainty in position,
$\boldsymbol{\Delta p}$ denotes the uncertainty in momentum,
$\boldsymbol{\hbar}$ is the reduced Planck’s constant, about $\boldsymbol{1.0545718 \times 10^{-34}}$ joule-second.

This relationship indicates that the product of the uncertainties in position and momentum cannot be smaller than half of the reduced Planck’s constant, highlighting the trade-off between measuring these properties with high precision.

Theoretical Implications

The principle is not merely a statement about experimental errors or a reflection of measurement techniques but a fundamental limit to what can be known about a particle’s properties. This inherent quantum uncertainty differentiates quantum mechanics from classical physics and has profound implications for the development of quantum theory.

Heisenberg’s γ-ray Microscope

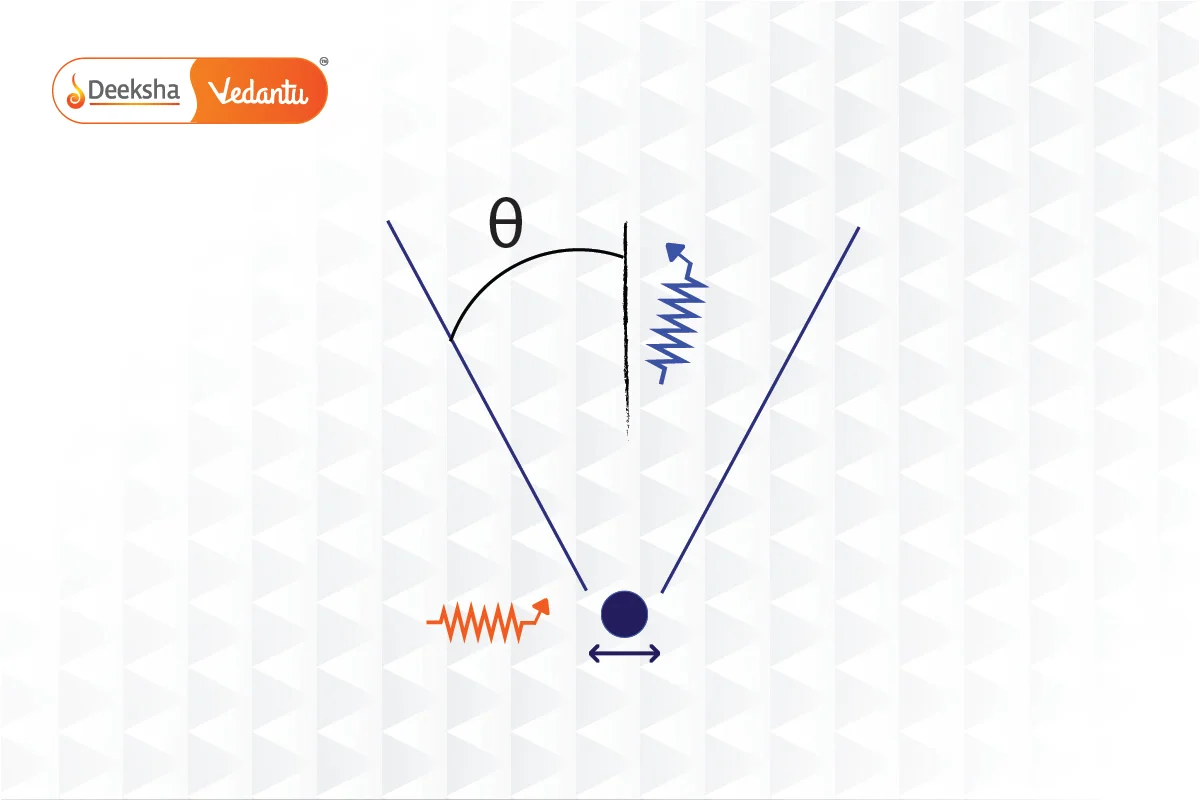
Heisenberg’s Gamma-ray Microscope is a conceptual tool devised to illustrate the principles of the Uncertainty Principle in quantum mechanics. Originally posited by Werner Heisenberg and further discussed by Niels Bohr, this thought experiment demonstrates the fundamental limits imposed by quantum mechanics on the precision of measurements.

Mechanism and Mathematical Analysis

Setup and Observational Strategy:

Gamma Rays: The microscope uses gamma rays of wavelength $\boldsymbol{\lambda}$ , which are directed at an electron. Gamma rays are chosen due to their extremely short wavelengths, which theoretically improve the resolving power of the microscope.
Microscope Objective: The diameter of the microscope objective subtends an angle $\boldsymbol{\theta}$ with respect to the electron. This configuration is crucial for capturing the scattered photons effectively.

Calculating Position Precision ( $\boldsymbol{\Delta x}$ ):

The precision with which the position of the electron can be determined, denoted as $\boldsymbol{\Delta x}$ , is influenced by the wavelength $\boldsymbol{\lambda}$ and the angle $\boldsymbol{\theta}$ . The resolving power formula for the microscope is: $\boldsymbol{\Delta x \approx \frac{\lambda}{2 \sin \theta}}$ .
Reducing $\boldsymbol{\lambda}$ or increasing $\boldsymbol{\sin \theta}$ seems to allow $\boldsymbol{\Delta x}$ to be minimized, enhancing the precision of position measurement.

Trade-off with Momentum Precision ( $\boldsymbol{\Delta p}$ ):

Compton Scattering: The scattered photon must remain within the cone of angle $\boldsymbol{\theta}$ to be detected. This condition introduces variability in the x-component of the photon’s momentum, which can vary within $\boldsymbol{\pm \frac{h}{\lambda \sin \theta}}$ , where $\boldsymbol{h}$ is Planck’s constant..
Implication for Electron’s Momentum: The electron recoils when it scatters the photon, leading to uncertainty in its momentum. The uncertainty in the electron’s momentum, $\boldsymbol{\Delta p}$ , is therefore affected by the same factors that influence the photon’s momentum: $\boldsymbol{\Delta p \geq \frac{h}{\lambda \sin \theta}}$ .

Heisenberg’s Uncertainty Principle Application:

The product of the uncertainties in position and momentum is then: $\boldsymbol{\Delta x \Delta p \geq \frac{h}{2}}$ .
This inequality shows that attempts to decrease $\boldsymbol{\Delta x}$ (increase position precision) result in an increase in $\boldsymbol{\Delta p}$ (less momentum precision), illustrating the core tenet of the Uncertainty Principle.

Real-World Applications and Impacts

Quantum Computing: The principle informs the behavior of qubits in quantum computing, where the state of particles is a critical element of processing and storing information.
Microscopy Techniques: In technologies such as electron microscopy, the principle limits the resolution, as high precision in position affects the clarity of momentum measurements.
Pharmaceuticals: Techniques based on nuclear magnetic resonance (NMR) rely on principles of quantum mechanics, including the uncertainty principle, to analyze molecular structures and interactions.

Practical Challenges and Considerations

The Uncertainty Principle challenges physicists to think creatively about how to measure and manipulate quantum systems. It necessitates the use of probabilistic models instead of deterministic ones, leading to new experimental designs and technologies that can accommodate or exploit these quantum limitations.

Conclusion

Heisenberg’s Uncertainty Principle is more than a quantum oddity; it’s a fundamental facet of the universe that tells us about the limits of observation and measurement. Understanding and applying this principle is crucial for advancing in fields that rely on quantum mechanics, from fundamental physics to practical applications in computing and beyond. As we delve deeper into the quantum world, the Uncertainty Principle remains a guiding factor in exploring the counterintuitive nature of reality at its most fundamental level.