Understanding Simple Harmonic Motion: Definitions, Types, and Applications

Understanding Simple Harmonic Motion

Simple Harmonic Motion (SHM) refers to a type of periodic and oscillatory motion where the restoring force is directly proportional to the negative of the displacement from the equilibrium position. This specific motion has characteristics that are important for various physical phenomena, such as sound waves, light waves, and electrical currents. The force always acts in the direction towards the equilibrium, helping maintain the motion’s cyclical nature.

Characteristics and Importance of SHM

Simple Harmonic Motion is characterized by its sinusoidal oscillations, where variables such as displacement, velocity, and acceleration change over time in a sinusoidal pattern. These oscillations are critical for understanding not only mechanical systems but also electromagnetic waves and alternating currents. Unlike general oscillatory motions, which might not be periodic, all SHM is inherently periodic, meaning it repeats after a fixed time interval.

Periodic, Oscillatory, and Harmonic Motions: Definitions and Differences

Periodic Motion: This occurs when an object moves in such a way that its motion repeats cyclically over time, like the orbit of planets or a swinging pendulum. The motion lacks a natural equilibrium as it continuously repeats without any restoring force.
Oscillatory Motion: This type of motion involves an object moving back and forth around a central or equilibrium point, such as a playground swing or a violin string. Oscillatory motion generally has a restoring force that pulls the system back towards its equilibrium point.
Simple Harmonic Motion: SHM is a specialized form of oscillatory motion where the path is linear, and the restoring force is directly proportional to the displacement from the mean position. SHM exhibits a unique stability at the mean position, making it a foundational concept in physics.

Types of Simple Harmonic Motion

SHM can manifest in two primary forms:

Linear SHM: Occurs when an object moves back and forth along a straight line, such as in a mass-spring system. The restoring force in this motion type is directly proportional to the displacement from the equilibrium and acts towards restoring equilibrium.
Angular SHM: This form involves rotational movements about a fixed axis, where the restoring torque is proportional to the angular displacement. Examples include a swinging door or a torsional pendulum.

Key Concepts in SHM

Amplitude: Represents the maximum displacement of an object from its equilibrium position.

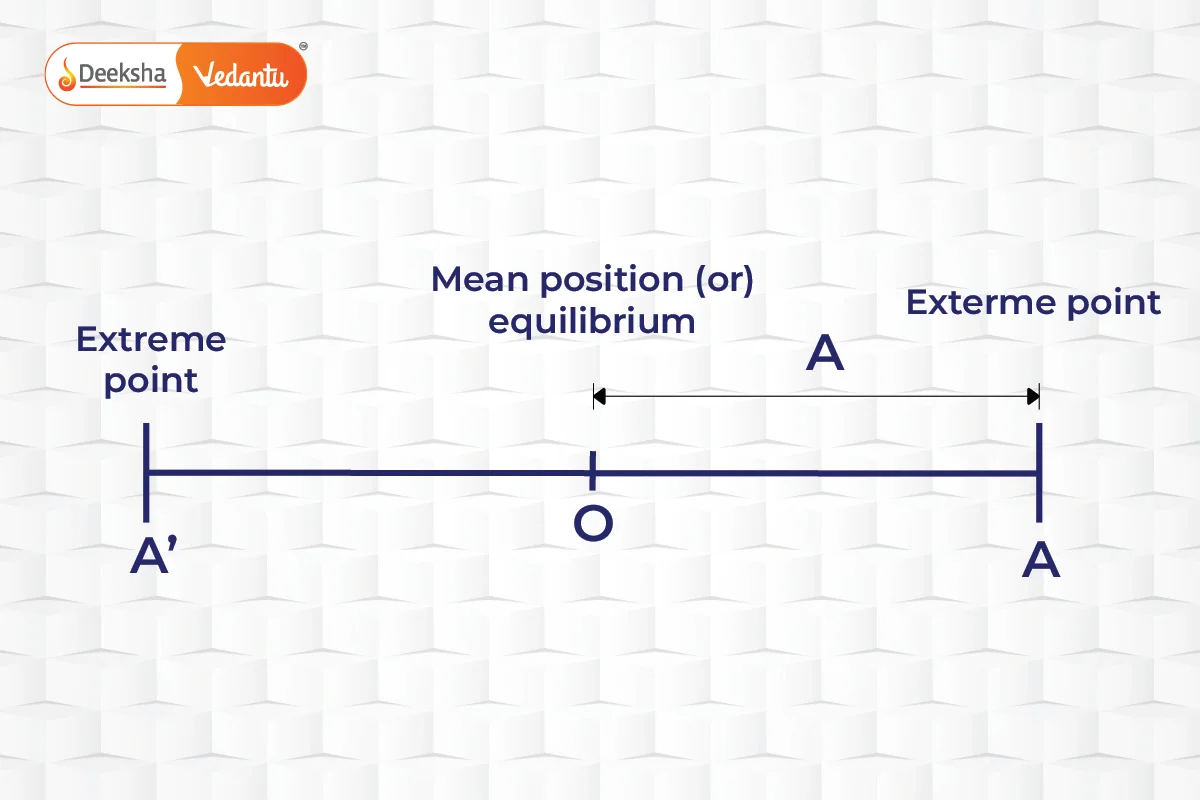
Period and Frequency: The period is the time it takes for one complete cycle of SHM, while frequency is the number of cycles per unit time. The relationship between angular frequency $\boldsymbol{(\omega)}$ , period $\boldsymbol{(T)}$ , and frequency $\boldsymbol{(f)}$ is defined by $\boldsymbol{\omega = 2\pi f = \frac{2\pi}{T}}$ .
Phase and Phase Difference: The phase determines the current state of the oscillation in terms of displacement and direction. Phase difference measures the difference in oscillation cycle between two points in motion, influencing how oscillations interact.

Equations and Dynamics of SHM

The dynamic behavior of SHM can be described by differential equations that consider factors like mass, velocity, and displacement. The solutions to these equations provide insights into the motion’s characteristics at any given moment, allowing for precise modeling of real-world oscillatory systems.

Necessary Conditions for Simple Harmonic Motion

$\bullet \ \boldsymbol{\vec{F} \propto -\vec{x}}$

$\bullet \ \boldsymbol{\vec{a} \propto -\vec{x}}$

$\bullet \ \boldsymbol{\vec{a} = -\omega^2 x}$

$\bullet \ \boldsymbol{\vec{a} = \frac{dv}{dx} \frac{dx}{dt} = v \frac{dv}{dx}}$

$\bullet \ \boldsymbol{\vec{a} = v \frac{dv}{dx} = -\omega^2 x}$

$\bullet \ \boldsymbol{\int_{0}^{v} v \, dv = \int_{0}^{x} -\omega^2 x \, dx}$

$\bullet \ \boldsymbol{\frac{v^2}{2} = -\frac{\omega^2 x^2}{2} + c \, \dots (1)}$

Some conditions we know:

At point A, v = 0 [x = A] the equation (1) becomes

$\bullet \ \boldsymbol{\frac{v^2}{2} = -\frac{\omega^2 A^2}{2} + c }$

Using, v = 0

$\boldsymbol{0 = \frac{-\omega^2 A^2}{2} + c}$

$\boldsymbol{c = \frac{\omega^2 A^2}{2}}$

Sub the value of C in equation (1)

$\boldsymbol{\frac{v^2}{2} = \frac{-\omega^2 x^2}{2} + \frac{\omega^2 A^2}{2}}$

$\boldsymbol{\Rightarrow v^2 = -\omega^2 x^2 + \omega^2 A^2}$

$\boldsymbol{\Rightarrow v^2 = \omega^2 \left(A^2 - x^2\right)}$

$\boldsymbol{v = \sqrt{\omega^2 \left(A^2 - x^2\right)}}$

$\boldsymbol{v = \omega \sqrt{A^2 - x^2} \, \ldots (2)}$

Where v is the velocity of the particle executing simple harmonic motion from the definition of instantaneous velocity

$\boldsymbol{v = \frac{dx}{dt} = \omega \sqrt{A^2 - x^2}}$

$\boldsymbol{\Rightarrow \int \frac{dx}{\sqrt{A^2 - x^2}} = \int_0^t \omega dt}$

$\boldsymbol{\Rightarrow \sin^{-1}\left(\frac{x}{A}\right) = \omega t + \phi}$

$\boldsymbol{x = A \sin (\omega t + \Phi) \, \ldots (3)}$

Equation (3) – Equation of the position of a particle as a function of time.

Case 1: If at t = 0

The particle at x = x0

$\boldsymbol{\Rightarrow \sin^{-1}\left(\frac{x}{A}\right) = \omega t + \phi}$

$\boldsymbol{\Rightarrow \sin^{-1}\left(\frac{x_0}{A}\right) = \phi}$

Φ is the initial phase of the particle.

Case 2: If at t = 0

The particle at x = 0

$\boldsymbol{\sin^{-1}\left(\frac{O}{A}\right) = \phi}$

i.e. Φ = 0

Case 3: If the particle is at one of its extreme positions, x = A at t = 0

$\boldsymbol{\Rightarrow \sin^{-1}\left(\frac{A}{A}\right) = \phi}$

$\boldsymbol{\Rightarrow \sin^{-1}(1) = \phi}$

$\boldsymbol{\Rightarrow \frac{\pi}{2} = \Phi}$

So, the value can be anything depending upon the position of the particle at t = 0. That is why it is called the initial phase of the particle

Now, if we se.e the equation of the position of the particle with respect to time,

$\boldsymbol{\frac{\pi}{2} = x = A \sin (\omega t + \Phi)}$

$\boldsymbol{\sin (\omega t + \Phi)}$ is the periodic function, whose period is $\boldsymbol{T = \frac{2\pi}{\omega}}$

Which can be anything, sine function or cosine function

Time Period of SHM

The coefficient of t is $\boldsymbol{\omega }$ .

So, the time period $\boldsymbol{T = \frac{2\pi}{\omega}}$

$\boldsymbol{\omega = \frac{2\pi}{T} = 2\pi f}$

$\boldsymbol{\omega t}$ = Angular frequency of SHM

From the expression of particle position as a function of time:

$\textbf{We can find particles, displacement}$ $\boldsymbol{\vec{x}}$ , $\textbf{velocity}$ $\boldsymbol{\vec{v}}$ $\textbf{and acceleration as follows.}$

The Velocity of a Particle Executing Simple Harmonic Motion

Velocity in SHM is given by $\boldsymbol{v = \frac{dx}{dt}}$ ,

$\boldsymbol{x = A \sin (\omega t + \Phi)}$

$\boldsymbol{v = \frac{d}{dt} A \sin (\omega t + \phi) = \omega A \cos (\omega t + \phi)}$

$\boldsymbol{v = A \omega \sqrt{1 - \sin^2 \omega t}}$

Since $\boldsymbol{x = A \sin \omega t}$

$\boldsymbol{\frac{x^2}{A^2} = \sin^2 \omega t}$

$\boldsymbol{\Rightarrow v = A \omega \sqrt{1 - \frac{x^2}{A^2}}}$

$\boldsymbol{\Rightarrow v = \omega \sqrt{A^2 - x^2}}$

On squaring both sides,

$\boldsymbol{\Rightarrow v^2 = \omega^2 \left(A^2 - x^2\right)}$

$\boldsymbol{\Rightarrow \frac{v^2}{\omega^2} = \left(A^2 - x^2\right)}$

$\boldsymbol{\Rightarrow \frac{v^2}{\omega^2 A^2} = \left(1 - \frac{x^2}{A^2}\right)}$

$\boldsymbol{\Rightarrow \frac{v^2}{A^2} + \frac{v^2}{A^2 \omega^2} = 1}$

this is an equation of an ellipse.

The curve between displacement and velocity of a particle executing the simple harmonic motion is an ellipse.

The Velocity of a Particle Executing Simple Harmonic Motion 2

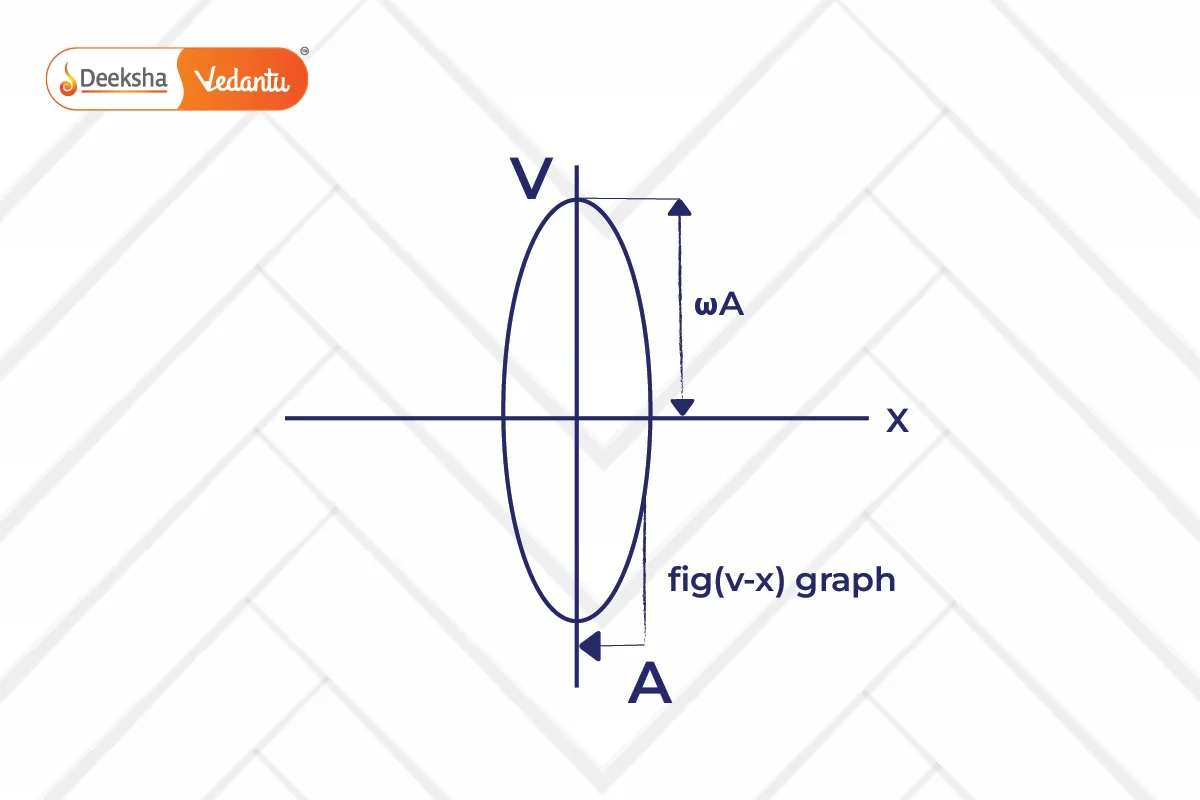
When $\boldsymbol{\omega = 1}$ , then the curve between v and x will be circular.

$\boldsymbol{\vec{a} = \frac{dv}{dt} = \frac{d}{dt} \left( A \omega \cos \omega t + \phi \right)}$

$\boldsymbol{\Rightarrow \vec{a} = -\omega^2 A \sin (\omega t + \phi)}$

$\boldsymbol{\Rightarrow |a| = -\omega^2 x}$

Acceleration in SHM

The Velocity of a Particle Executing Simple Harmonic Motion 1

Hence, the expression for displacement, velocity and acceleration in linear simple harmonic motion is

$\bullet \ \boldsymbol{x = A \sin (\omega t + \Phi)}$

$\bullet \ \boldsymbol{v = A \omega \cos (\omega t + \phi) = \omega \sqrt{A^2 - x^2}}$

$\bullet \ \boldsymbol{a = -A \omega^2 \sin (\omega t + \phi) = -\omega^2 x}$

Energy in Simple Harmonic Motion (SHM)

The system that executes SHM is called the harmonic oscillator.

Consider a particle of mass m, executing linear simple harmonic motion of angular frequency $\boldsymbol{(\omega)}$ and amplitude $\boldsymbol{(A)}$ ,

$\textbf{the displacement}$ $\boldsymbol{\vec{x}}$ , $\textbf{velocity}$ $\boldsymbol{\vec{v}}$ $\textbf{and acceleration}$ $\boldsymbol{\vec{a}}$ $\textbf{at any time t are given by}$

$\boldsymbol{x = A \sin (\omega t + \Phi)}$

$\boldsymbol{v = A \omega \cos (\omega t + \phi) = \omega \sqrt{A^2 - x^2}}$

$\boldsymbol{a = -\omega^2 A \sin (\omega t + \phi) = -\omega^2 x}$

$\textbf{The restoring force}$ $\boldsymbol{\vec{F}}$ $\textbf{acting on the particle is given by}$

$\boldsymbol{F = -kx, \text{ where } k = m\omega^2}$

Kinetic Energy of a Particle in SHM

$\boldsymbol{= \frac{1}{2} mv^2 \quad \left[ \text{Since, } v^2 = A^2 \omega^2 \cos^2 (\omega t + \phi) \right]}$

$\boldsymbol{= \frac{1}{2} m \omega^2 A^2 \cos^2 (\omega t + \phi)}$

$\boldsymbol{= \frac{1}{2} m \omega^2 (A^2 - x^2)}$

$\textbf{Therefore, the Kinetic Energy}$

$\boldsymbol{= \frac{1}{2} m \omega^2 A^2 \cos^2 (\omega t + \phi) = \frac{1}{2} m \omega^2 (A^2 - x^2)}$

Potential Energy of SHM

The total work done by the restoring force in displacing the particle from (x = 0) (mean position) to x = x:

When the particle has been displaced from x to x + dx, the work done by restoring force is

$\boldsymbol{dw = F \, dx = -kx \, dx}$

$\boldsymbol{w = \int dw = \int_0^x -kxdx = \frac{-kx^2}{2}}$

$\boldsymbol{= \frac{-m\omega^2 x^2}{2}}$

$\boldsymbol{\left[k = m\omega^2\right]}$

$\boldsymbol{= \frac{-m\omega^2}{2} A^2 \sin^2 (\omega t + \phi)}$

$\textbf{Potential Energy}$ $\boldsymbol{= -(\text{work done by restoring force})}$

$\boldsymbol{= \frac{m\omega^2 x^2}{2} = \frac{m\omega^2 A^2}{2} \sin^2 (\omega t + \phi)}$

Total Mechanical Energy of the Particle Executing SHM

$\textbf{E = KE + PE}$

$\boldsymbol{E = \frac{1}{2} m \omega^2 \left( A^2 - x^2 \right) + \frac{1}{2} m \omega^2 x^2}$

$\boldsymbol{E = \frac{1}{2} m \omega^2 A^2}$

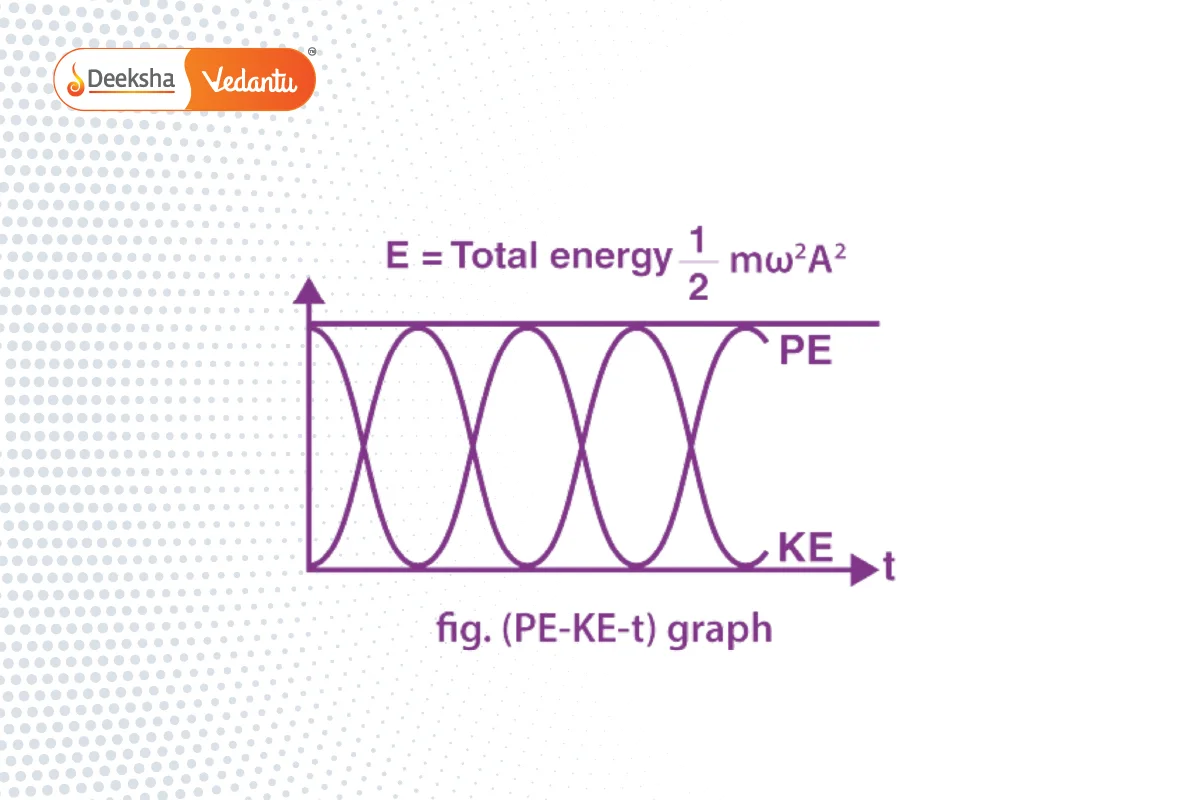
Hence, the particle’s total energy in SHM is constant, independent of the instantaneous displacement.

⇒ Relationship between kinetic energy, potential energy and time in Simple Harmonic Motion at t = 0, when x = ±A.

Total Mechanical Energy of the Particle Executing SHM 2

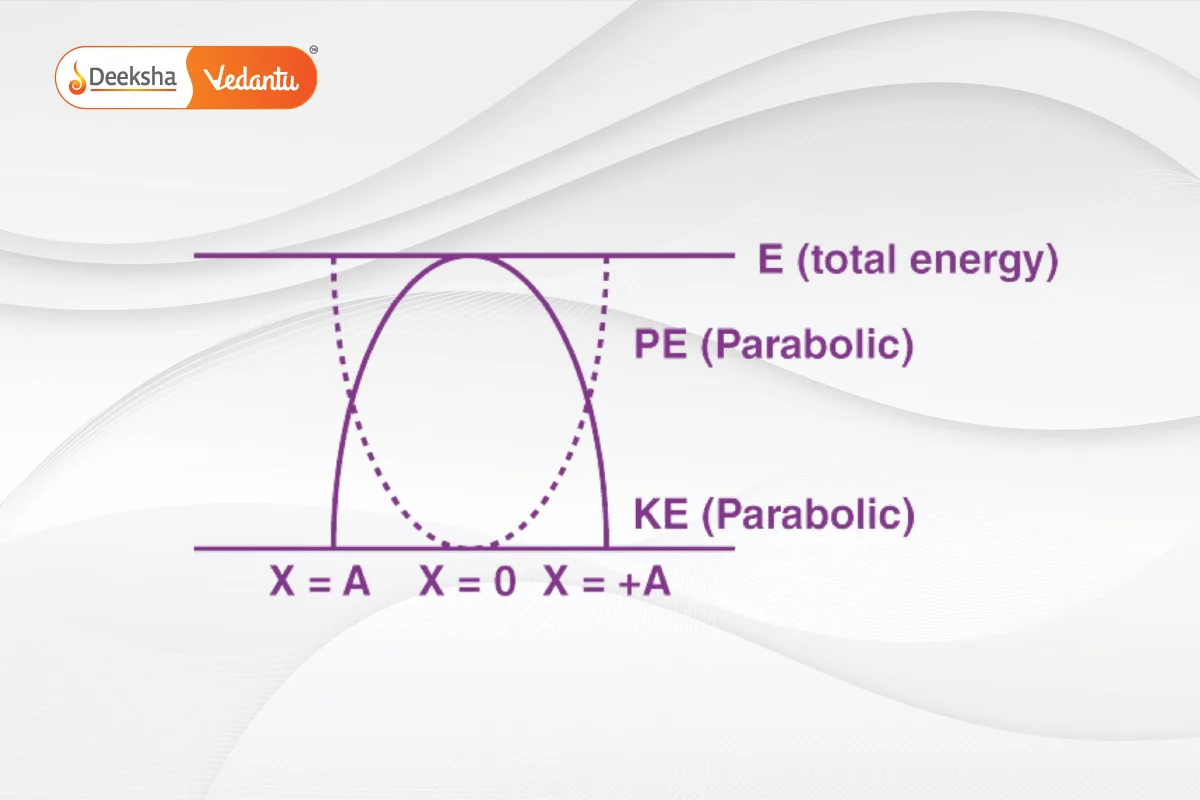
⇒ Variation of kinetic energy and potential energy in Simple Harmonic Motion with displacement.

Total Mechanical Energy of the Particle Executing SHM 1

Practical Applications and Examples of SHM

Pendulums and Springs: Common in clocks and measuring instruments where precise periodicity is crucial.
Mechanical Oscillators: Used in various engineering applications, including sensors and vibration absorbers.
Electrical Oscillators: Form the basis of many electronic devices, such as radios and computers, where they generate repetitive electronic signals.