Explore Pythagoras Theorem: Applications and Proof

Understanding Pythagoras Theorem: The Fundamental Relationship in Right-Angled Triangles

Pythagoras Theorem, named after the ancient Greek mathematician Pythagoras, is a fundamental principle in geometry that describes the relationship between the three sides of a right-angled triangle. This theorem is a staple in mathematical education, providing a basis for learning about the properties of right triangles.

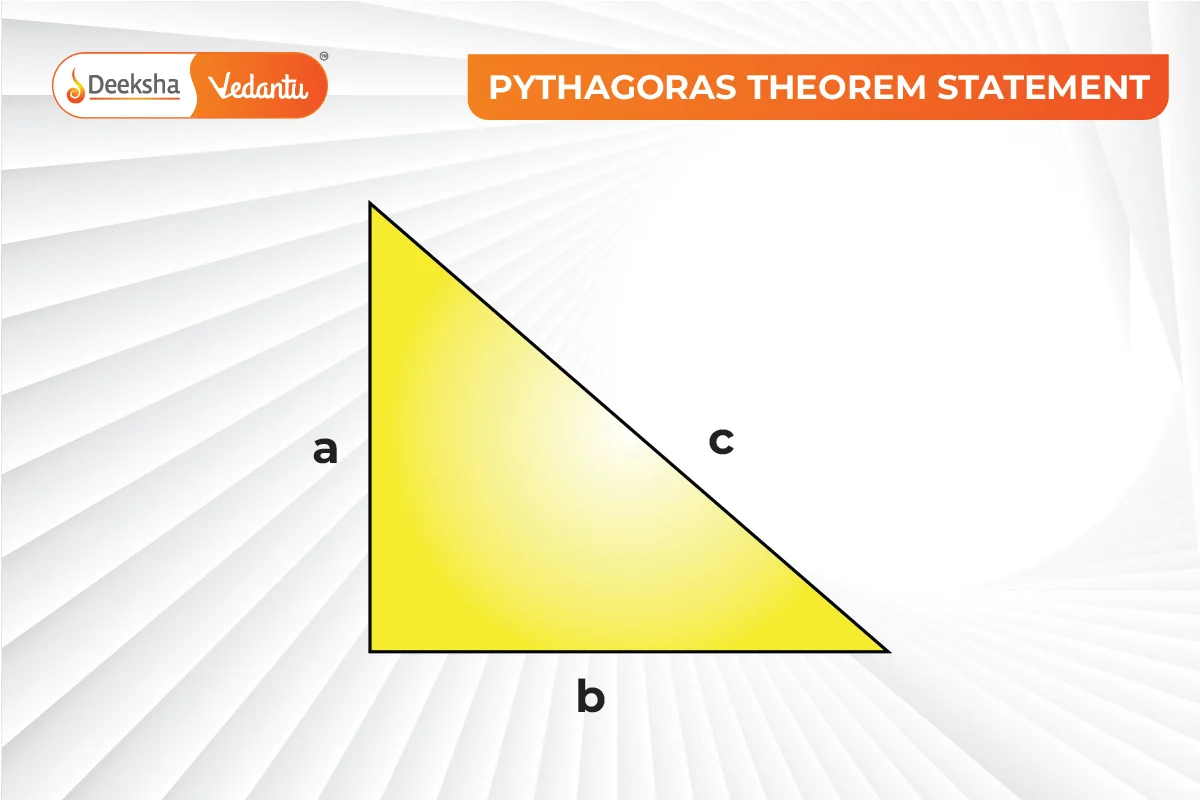
The theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This relationship is expressed in the formula:

$\boldsymbol{c^2 = a^2 + b^2}$

where c is the hypotenuse, and a and b are the other two sides of the triangle.

Historical Background

Pythagoras, a Greek mathematician, is credited with the popularization of this theorem, which has been used since ancient times.

Formula and Application

The Pythagoras theorem is pivotal for calculating the unknown length of a side in a right-angled triangle when the lengths of the other two sides are known. This is especially useful in various fields such as architecture, astronomy, and physics.

Pythagoras Theorem Formula:

Hypotenuse squared = Perpendicular squared + Base squared
$\boldsymbol{c^2 = a^2 + b^2}$

Proof of Pythagoras Theorem

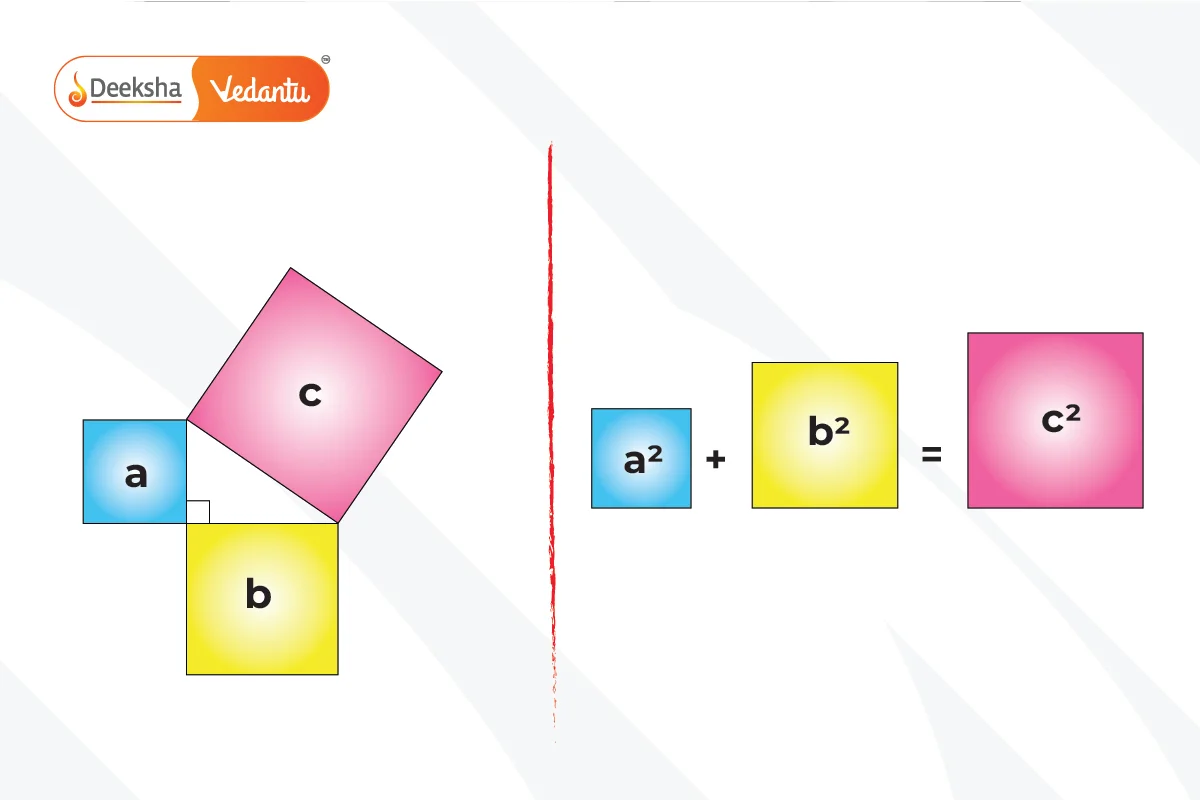
The proof involves comparing the areas of squares constructed on each of the three sides of the triangle. The area of the square on the hypotenuse is shown to be equal to the sum of the areas of the squares on the other two sides.

Applications of Pythagoras Theorem:

Determining Right Triangles: Check if a triangle with sides of given lengths is a right triangle.
Calculating Side Lengths: Find an unknown side length in a right-angled triangle when the other two side lengths are known.
Diagonal Calculations: Calculate the diagonal of a square, which is a common application in construction and design.

Example Problems:

Finding a Side Length: For a right triangle with sides 3 cm and 4 cm, and a hypotenuse to be determined, use the theorem to find that the hypotenuse is 5 cm.
Verifying a Right Triangle: For a triangle with sides 5, 12, and 13 units, verify if it is a right triangle by applying the theorem. The sums of the squares of the two shorter sides will equal the square of the longest side, confirming it’s a right triangle.
Diagonal of a Square: Given a square with a side length of 4 cm, use the theorem to find that the diagonal is 4√2 cm.

How to Use Pythagoras Theorem:

To apply the theorem:

Identify the sides of the right triangle.
Apply the formula $\boldsymbol{c^2 = a^2 + b^2}$
Solve for the unknown side or verify the properties of the triangle.

Determining if a Triangle is Right-Angled:

Using the lengths of the three sides, apply the Pythagoras theorem. If the square of the longest side equals the sum of the squares of the other two sides, the triangle is right-angled.