Understanding Mensuration in Mathematics
Mensuration is the mathematical field that involves calculating the parameters of geometric figures, including their area, volume, and perimeter. This area of study is essential in mathematics as it bridges daily practical applications with mathematical theory. From the architecture around us to the objects we use, understanding the dimensions and properties of shapes enhances our interaction with the world.
What is Mensuration?
Mensuration is a branch of mathematics focused on the measurement of various geometric figures. It deals with the calculation of lengths, areas, and volumes of both two-dimensional (2D) and three-dimensional (3D) shapes. This field is divided into two categories:
- 2D Mensuration: Involves flat shapes like squares, circles, and triangles, where measurements include area and perimeter.
- 3D Mensuration: Deals with solid objects like cubes, cylinders, and spheres, focusing on volume and surface area measurements.
Key Concepts and Definitions in Mensuration
- Area: The measure of the space enclosed within a shape, typically measured in square units (m² or cm²).
- Perimeter: The total length of the boundary of a 2D shape.
- Volume: The amount of space occupied by a 3D object, measured in cubic units (m³ or cm³).
- Surface Area: The total area that the surface of a 3D object occupies.
- Curved/Lateral Surface Area: The area of the curved surface of a 3D object, excluding its bases.
Mensuration Formulas
Mensuration involves a variety of formulas to calculate the dimensions of different shapes:
- 2D Shapes:
- Square:
- Square:

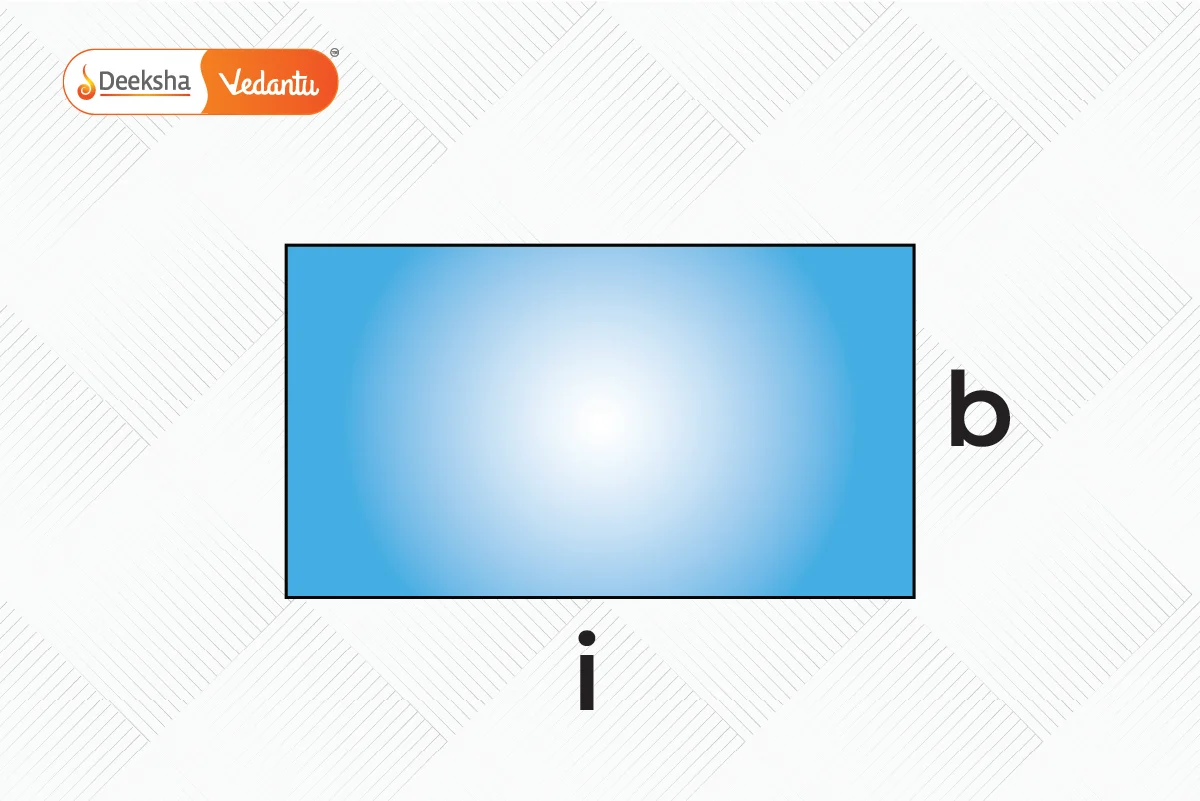
- Rectangle:
- Rectangle:
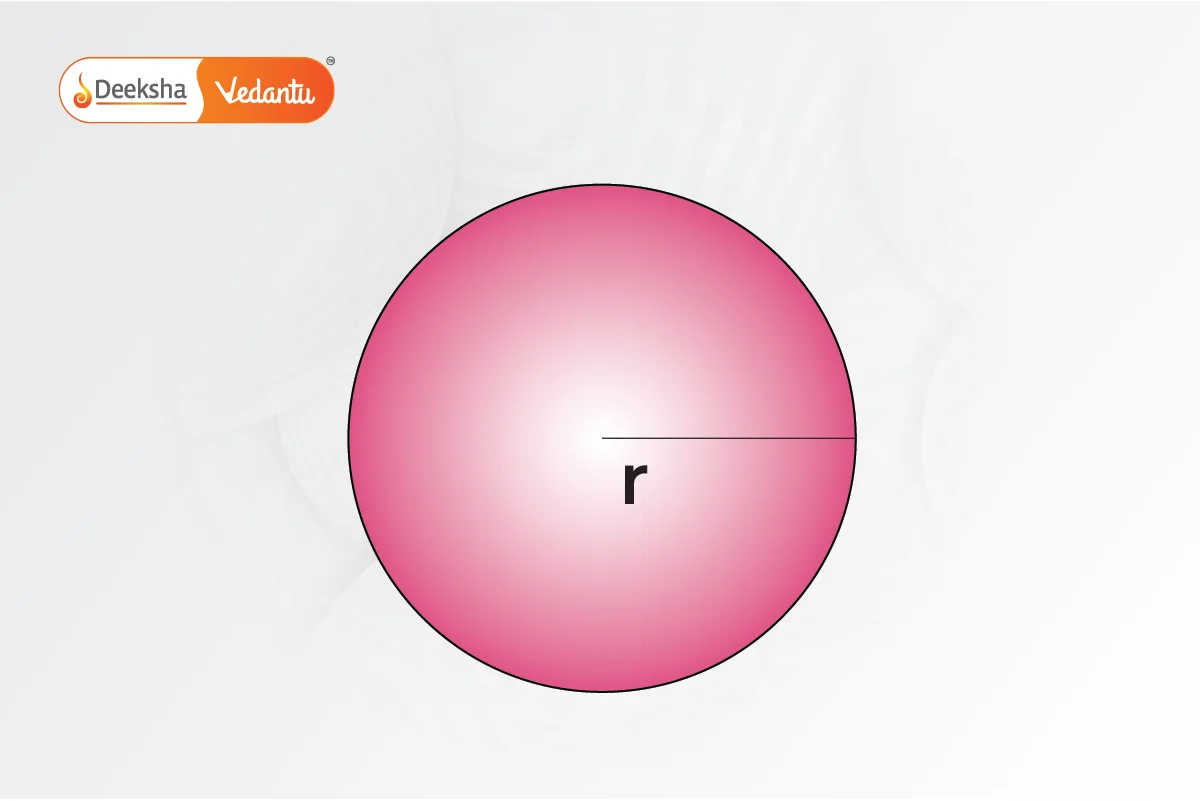
- Circle:
- Circle:
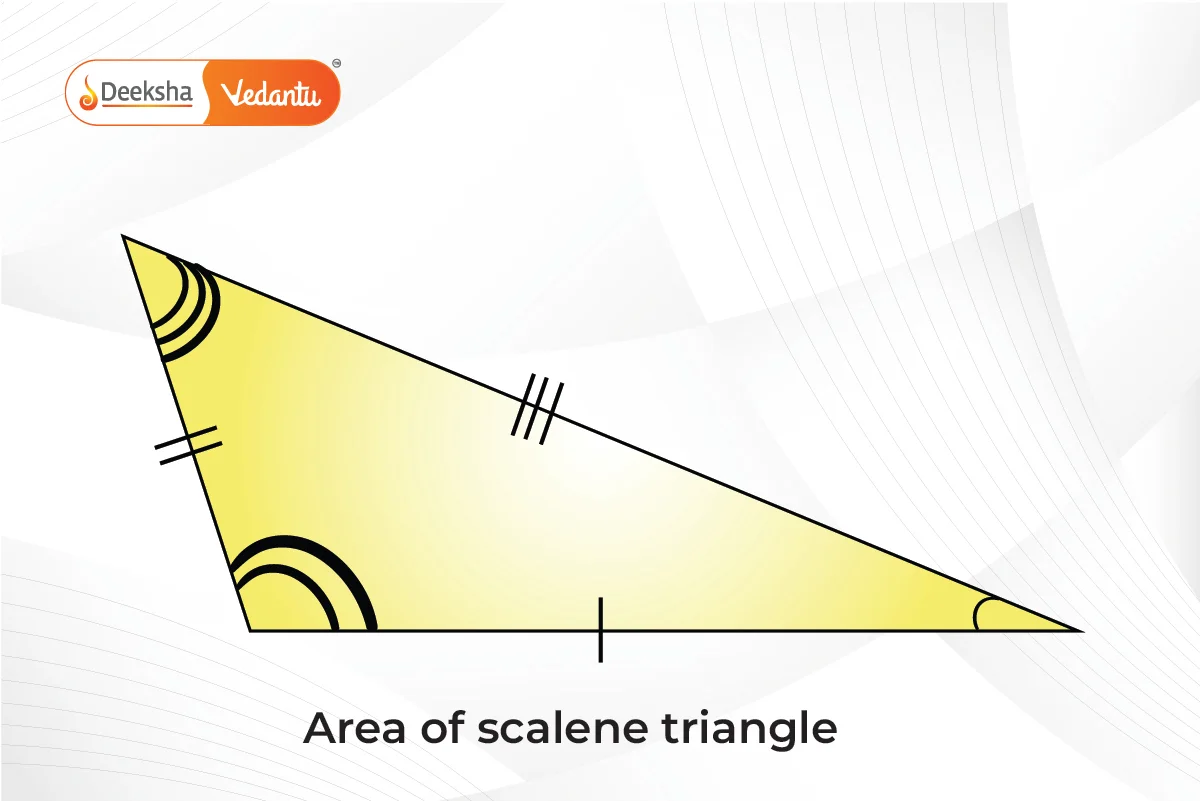
- Scalene Triangle:
- Scalene Triangle:
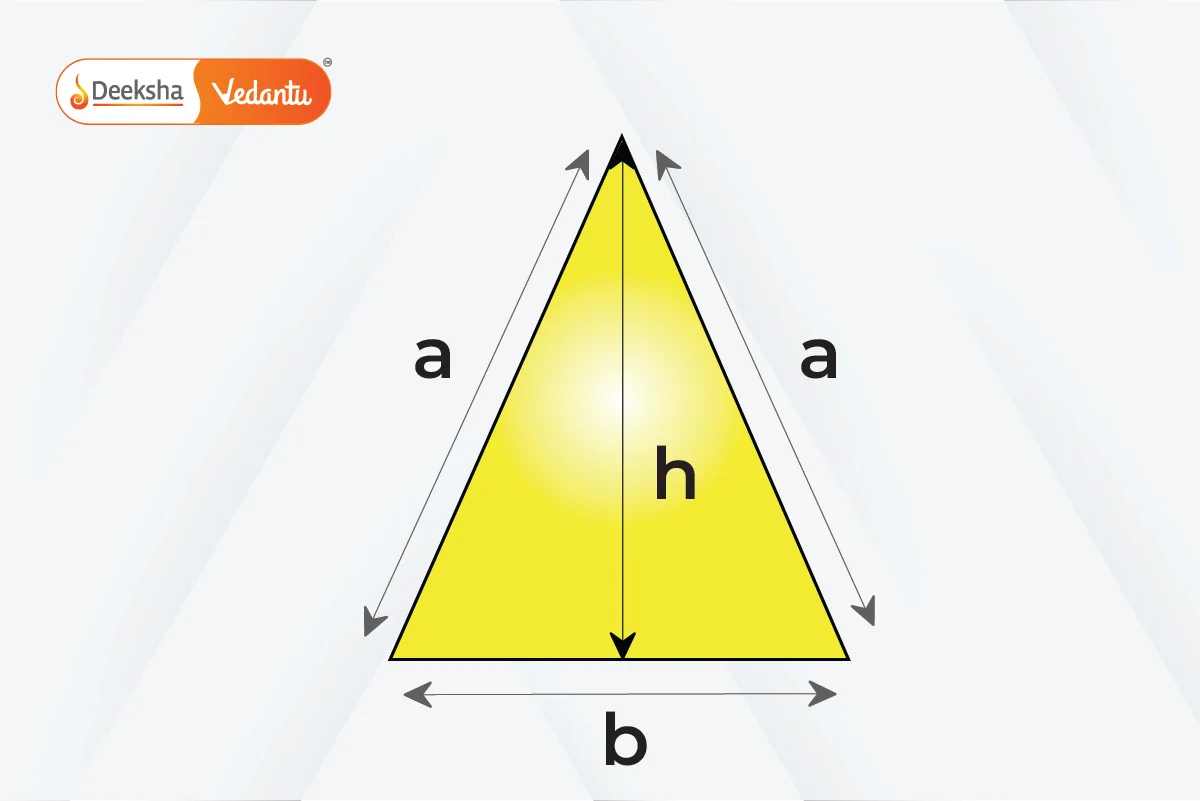
- Isosceles Triangle:
- Isosceles Triangle:
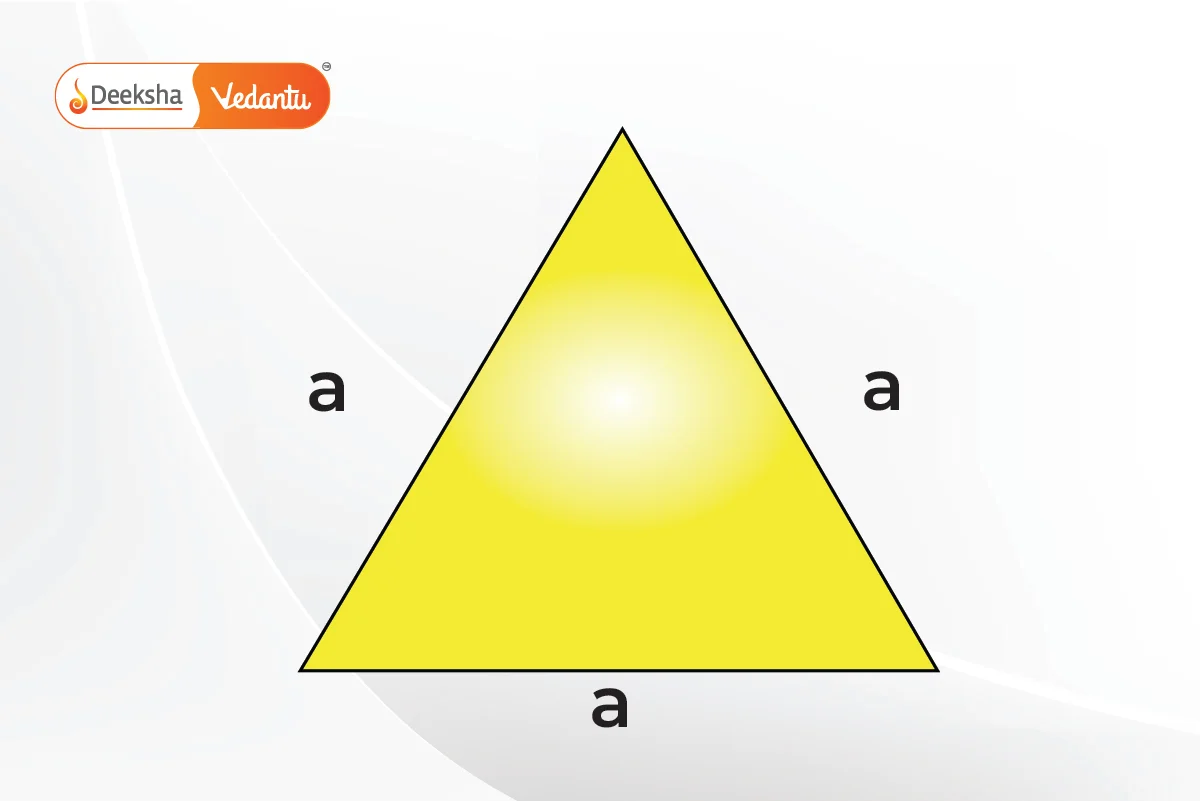
- Equilateral triangle:
- Equilateral triangle:
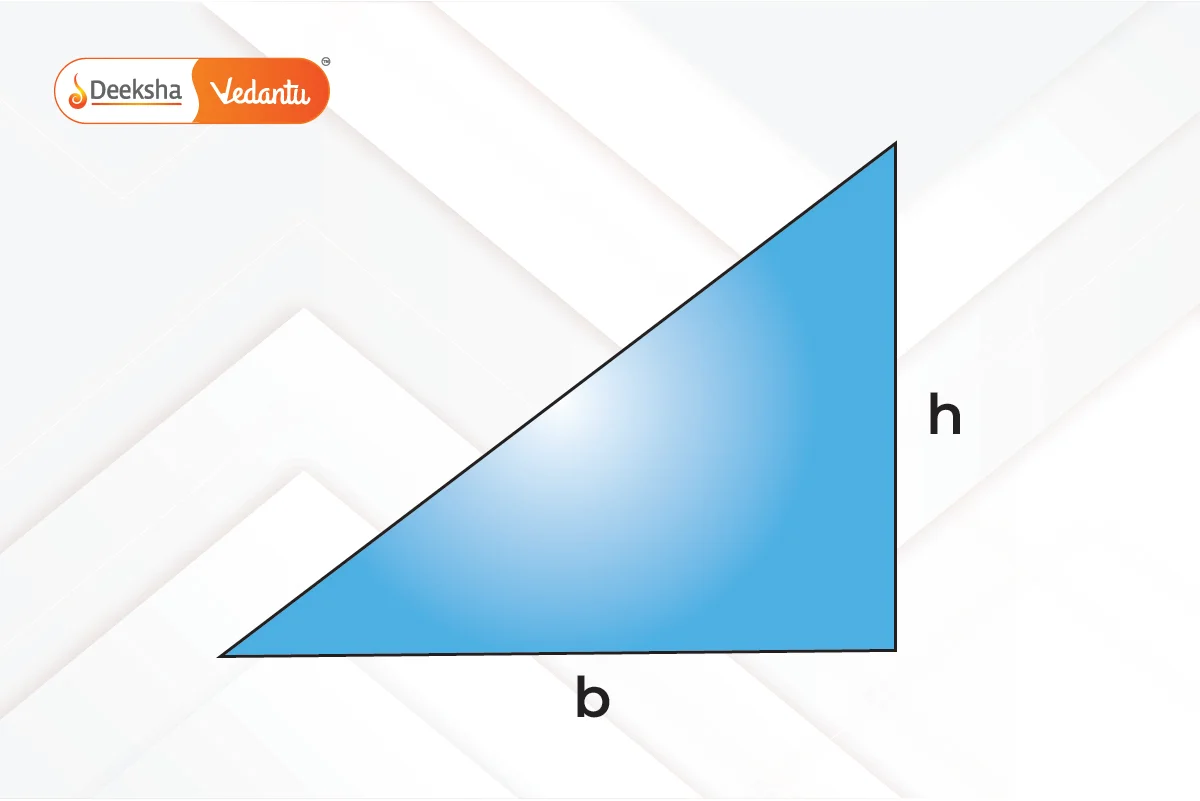
- Right Angle Triangle:
- Right Angle Triangle:
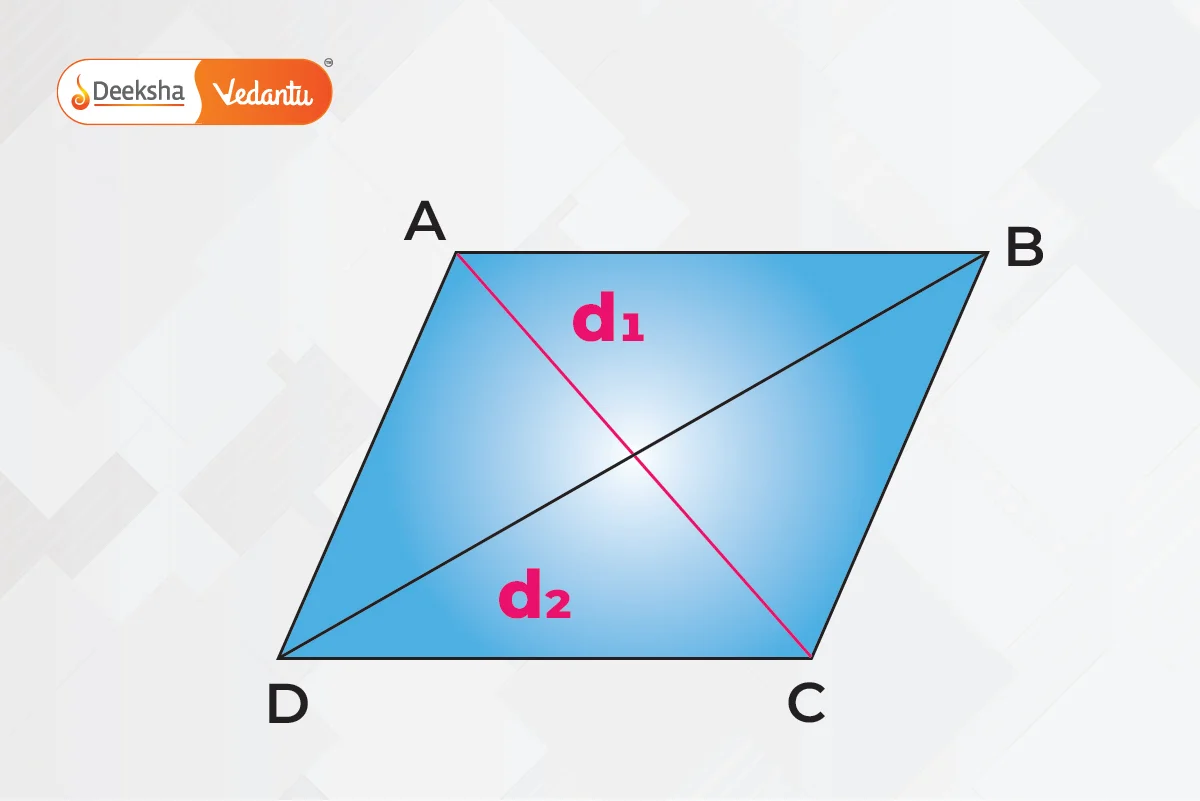
- Rhombus:
- Rhombus:
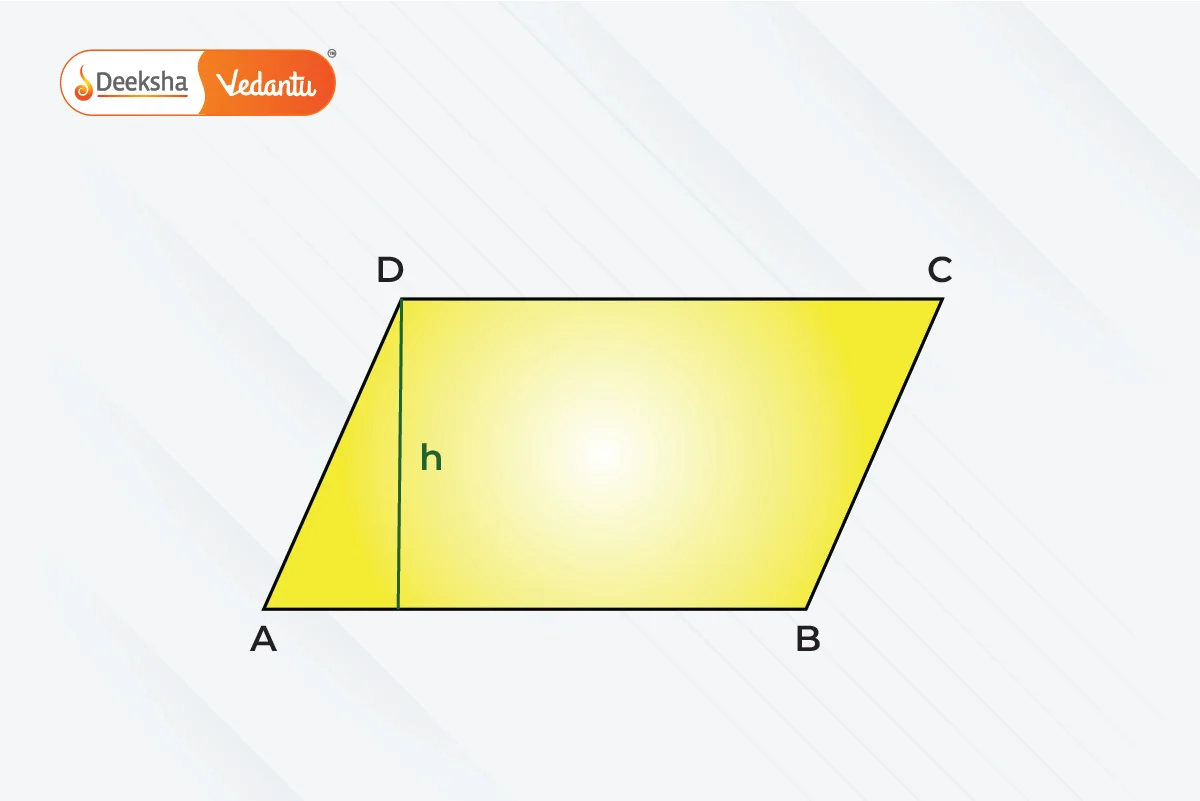
- Parallelogram:
- Parallelogram:
- Trapezium:
- Trapezium:
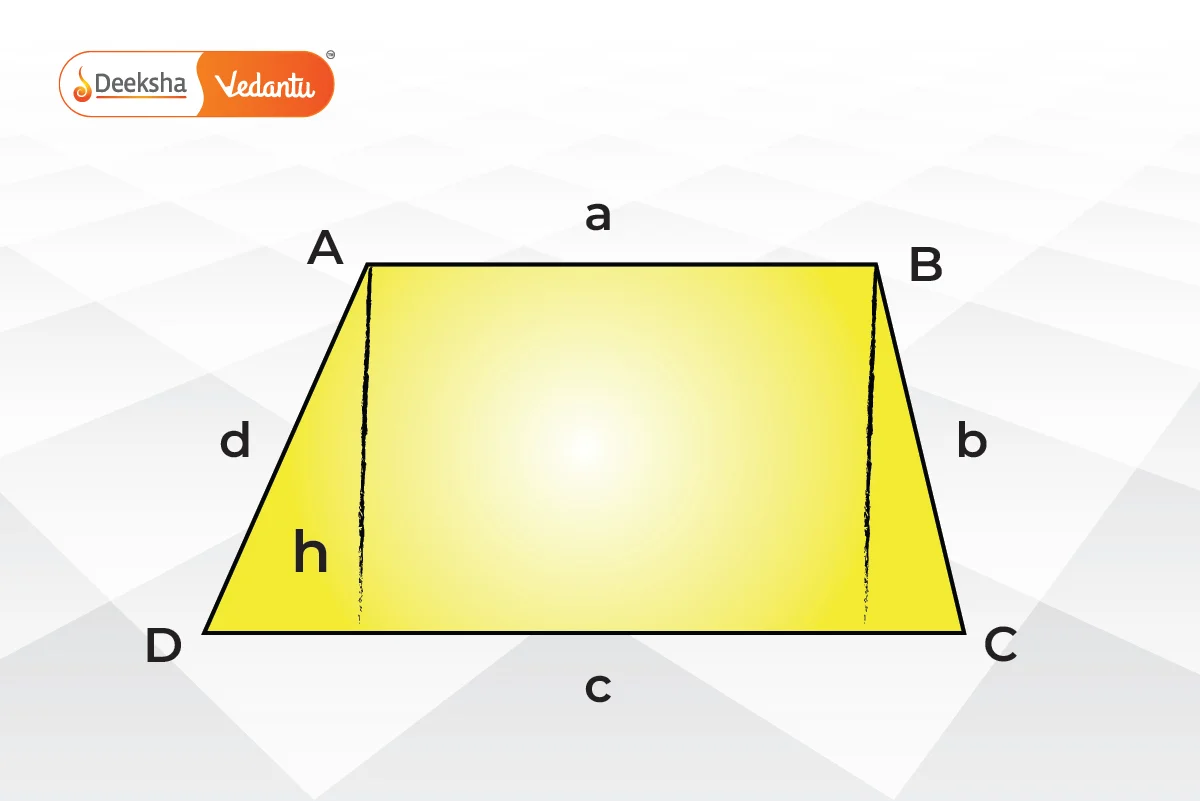
- 3D Shapes:
- Cube:
- Cube:

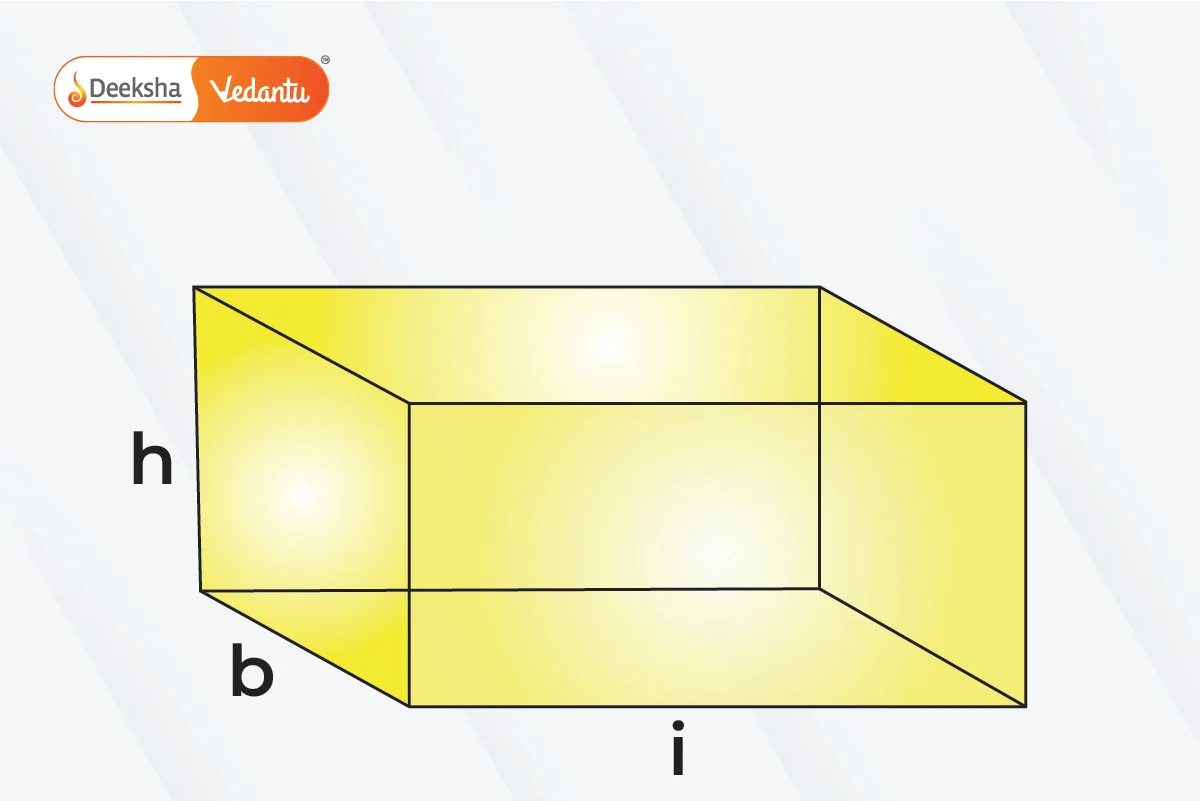
- Cuboid:
- Cuboid:
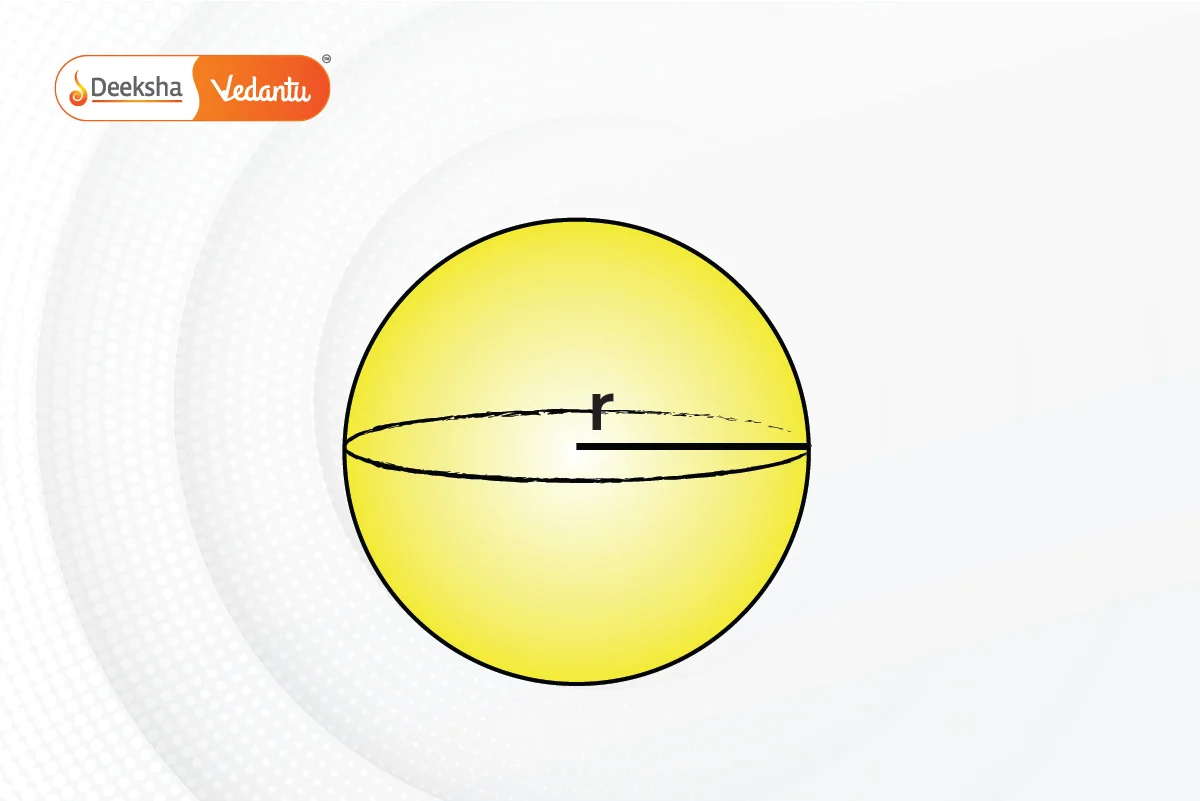
- Sphere:
- Sphere:
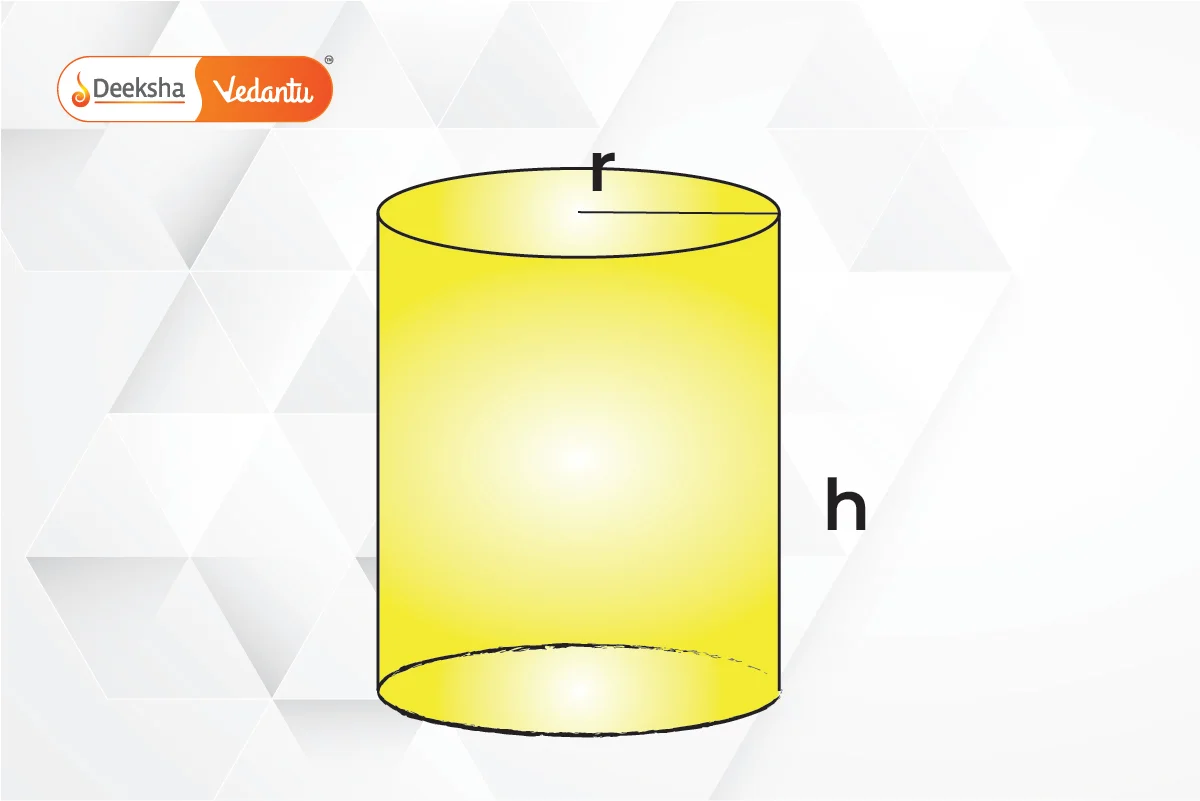
- Cylinder:
- Cylinder:
Applications of Mensuration
Mensuration is crucial in various real-life applications:
- Architecture and Construction: Calculating the materials required for construction.
- Engineering: Designing parts and devices with specific dimensions.
- Everyday Life: Determining the amount of paint needed for a room or the fabric for making a dress.
Learning Mensuration
Understanding mensuration requires practice and familiarity with geometric principles. Tools like diagrams, models, and interactive software can help visualize and solve mensuration problems effectively. Practicing through worksheets and applying mensuration in practical scenarios enhances comprehension and retention of the concepts.
Further Exploration in Mensuration
For those interested in delving deeper, exploring advanced topics such as the mensuration of complex figures and integration in calculus for finding areas and volumes can be quite enriching. Educational resources and tools from Deeksha Learning provide a comprehensive platform for studying these advanced concepts.
FAQs
Yes, mensuration formulas can be extended to irregular shapes using advanced mathematical techniques like calculus, particularly for integrating areas and volumes.
The volume of a 3D object is the space it occupies, measured in cubic units, while the surface area is the total area covered by the surface of the object, measured in square units.
The area of a circle can be calculated using the formula , where “r” is the radius of the circle.
Mensuration is vital for practical applications in fields like engineering, construction, and daily life tasks such as calculating space in home projects or material requirements.
Mensuration is the branch of mathematics that deals with the measurement of various parameters of geometric figures, including area, volume, and perimeter.










Get Social