Understanding Rational Numbers: Definitions, Properties, and Examples

A rational number is a real number that can be expressed as a fraction p/q, where q is not zero. Examples include 1/2, 1/5, and 3/4. The number “0” is also a rational number because it can be written as 0/1, 0/2, etc. However, fractions like 1/0 are not rational since they are undefined.

What is a Rational Number?

In math, a rational number is any number that can be written as p/q, where q≠0q. Both the numerator p and the denominator q are integers. When you divide the fraction, the result will be a decimal that either terminates or repeats.

Identifying Rational Numbers

To determine if a number is rational, check if it:

Can be written as p/q, with q≠0.
Can be simplified to a decimal form.

Examples of Rational Numbers

p	q	qp/q
10	2	10/2 = 5
1	1000	1/1000 = 0.001
50	10	50/10 = 5

Types of Rational Numbers

Rational numbers include positive, negative numbers, and zero. They can all be written as fractions.

Real numbers (R) include all the rational numbers (Q).
Real numbers include the integers (Z).
Integers involve natural numbers(N).
Every whole number is a rational number because every whole number can be expressed as a fraction.

Standard Form of Rational Numbers

A rational number is in standard form when the numerator and denominator have no common factors other than 1, and the denominator is positive. For example, 12/36 simplifies to 1/3.

Positive and Negative Rational Numbers

Rational numbers can be positive or negative. If both numerator and denominator are positive, the number is positive. If one is negative, the number is negative.

Positive Rational Numbers	Negative Rational Numbers
Same sign for numerator and denominator	Opposite signs for numerator and denominator
Greater than 0	Less than 0
Examples: 12/17, 9/11, 3/5	Examples: -2/17, 9/-11, -1/5

Arithmetic Operations on Rational Numbers

Addition: $\boldsymbol{\frac{p}{q} + \frac{s}{t} = \frac{pt + qs}{qt}}$
- - Example: $\boldsymbol{\frac{1}{2} + \frac{3}{4} = \frac{2 + 3}{4} = \frac{5}{4}}$

Subtraction: $\boldsymbol{\frac{p}{q} - \frac{s}{t} = \frac{pt - qs}{qt}}$
- - Example: $\boldsymbol{\frac{1}{2} - \frac{3}{4} = \frac{2 - 3}{4} = \frac{-1}{4}}$

Multiplication: $\boldsymbol{\frac{p}{q} \times \frac{s}{t} = \frac{p \times s}{q \times t}}$
- - Example: $\boldsymbol{\frac{1}{2} \times \frac{3}{4} = \frac{1 \times 3}{2 \times 4} = \frac{3}{8}}$

Division: $\boldsymbol{\frac{p}{q} \div \frac{s}{t} = \frac{p \times t}{q \times s}}$
- - Example: $\boldsymbol{\frac{1}{2} \div \frac{3}{4} = \frac{1 \times 4}{2 \times 3} = \frac{4}{6} = \frac{2}{3}}$

Multiplicative Inverse of Rational Numbers

The multiplicative inverse of p/q is q/p. For example, the inverse of 4/7 is 7/4.

Properties of Rational Numbers

Adding, subtracting, or multiplying two rational numbers always gives a rational number.
A rational number stays the same if both numerator and denominator are multiplied or divided by the same factor.
Adding zero to a rational number keeps it the same.
Rational numbers are closed under addition, subtraction, and multiplication.

Rational vs. Irrational Numbers

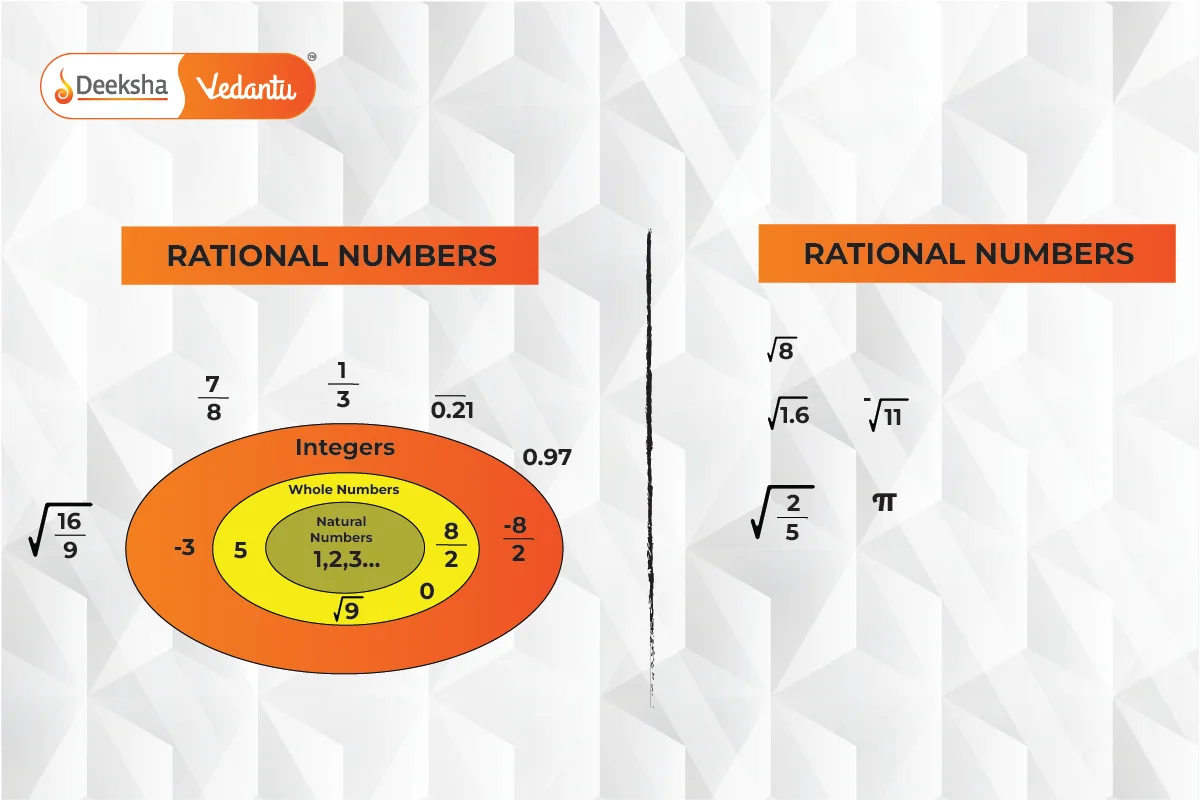
A rational number can be written as a fraction with a non-zero denominator. An irrational number cannot be expressed as a simple fraction and has an endless, non-repeating decimal. Examples of irrational numbers include:

Pi (π) = 3.142857…
Euler’s Number (e) = 2.7182818284590452…
√2 =1.414213…

Finding Rational Numbers Between Two Rational Numbers

There are infinite rational numbers between any two rational numbers. You can find them by:

Finding Equivalent Fractions: For example, between 1/2 and 3/4, you can use 2/4 and 3/4 to identify numbers in between.
Finding the Mean: The mean value between two rational numbers is also a rational number. Repeat this process to find more rational numbers between them.