Introduction
Real numbers include all numbers that can be represented on a number line, encompassing both rational and irrational numbers. Rational numbers are those that can be expressed as , where
and
are integers, and
. They include integers, fractions, and decimals that either terminate or repeat. Irrational numbers, on the other hand, cannot be expressed as fractions. They have non-terminating, non-recurring decimal expansions and include numbers like
,
, and
. The concept of real numbers forms the foundation for understanding various mathematical principles and applications, especially in the field of algebra and geometry.

Definition and Classification
Real numbers include all the numbers that can occupy a position on the number line. These are categorized into two major types:
- Rational Numbers: Numbers that can be expressed as a fraction where both the numerator and the denominator are integers, and the denominator is not zero.
- Irrational Numbers: Numbers that cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal parts.
Subcategories of Real Numbers:
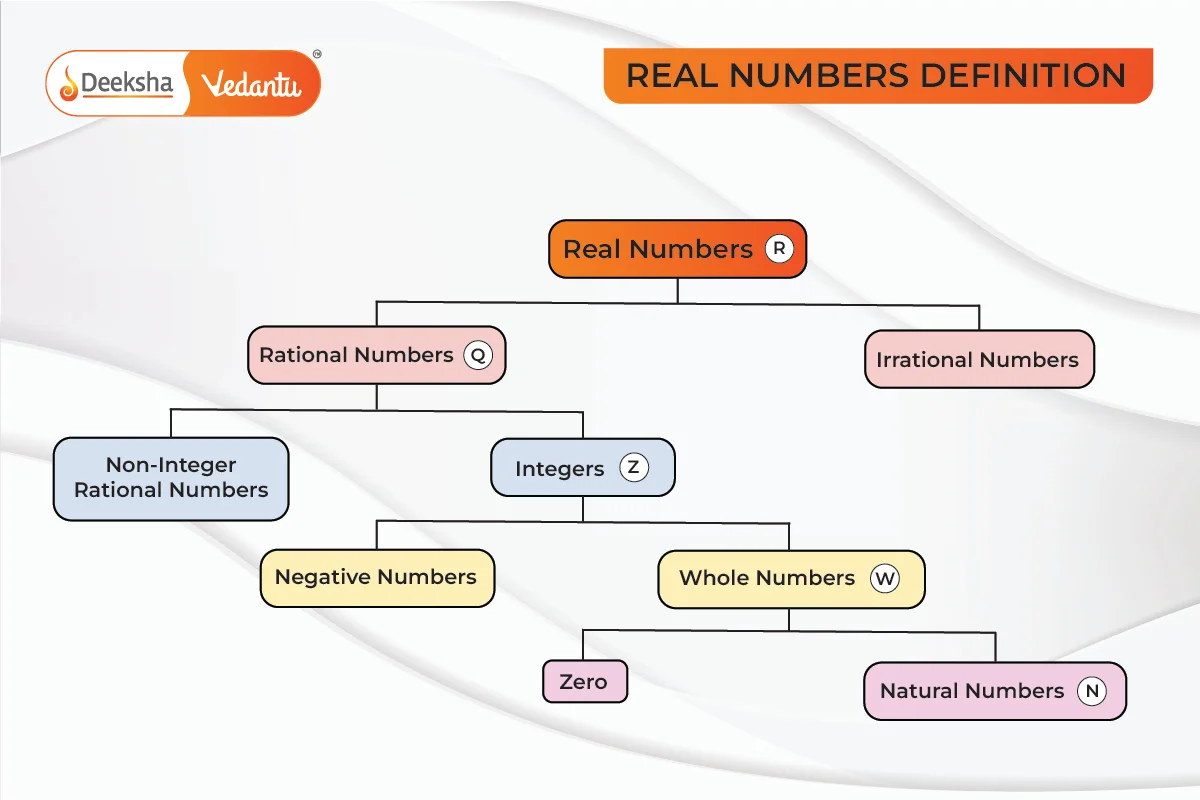
- Natural Numbers (N): Positive integers starting from 1 (1, 2, 3, …)
- Whole Numbers (W): All natural numbers including zero (0, 1, 2, 3, …)
- Integers (Z): All positive and negative whole numbers, including zero (-3, -2, -1, 0, 1, 2, 3, …)
- Rational Numbers (Q): Numbers expressed as a fraction (1/2, 2/3, 5/4)
- Irrational Numbers: Non-repeating, non-terminating decimals (π, √2)
Properties of Real Numbers
Real numbers follow several algebraic properties which facilitate the ease of computation and algebraic manipulations:
| Property | Operation | Expression |
| Commutative Property | Addition | |
| Multiplication | ||
| Associative Property | Addition | |
| Multiplication | ||
| Distributive Property | – | |
| Identity Property | Addition | |
| Multiplication |
Euclid’s Division Lemma
Euclid’s Division Lemma is a fundamental mathematical tool that helps us express a number as a product of another number plus a remainder. It states that for any two positive integers and
, there exist unique integers
(quotient) and
(remainder) such that:
where
This lemma is the basis for the Euclidean Algorithm, which is commonly used to find the Highest Common Factor (HCF) of two numbers. By repeatedly applying Euclid’s Division Lemma, we divide the larger number by the smaller, continue with the remainder, and repeat this process until the remainder is zero. The last non-zero remainder is the HCF of the two numbers.
Example: To find the HCF of 135 and 225 using Euclid’s Division Lemma:
Since the remainder has become zero, the last non-zero remainder is 45, so the HCF of 135 and 225 is 45.
This method of using Euclid’s Division Lemma is efficient and forms the basis of more advanced algorithms in mathematics, especially in number theory and cryptography.
The Fundamental Theorem of Arithmetic
The Fundamental Theorem of Arithmetic states that every composite number can be expressed uniquely (except for the order of factors) as a product of prime numbers. This means that each number can be “broken down” into a multiplication of prime factors, which are its building blocks. Prime factorization is not only unique for each number but also important in finding the HCF and Least Common Multiple (LCM) of numbers.
Prime factorization provides an insight into the structure of numbers and is used in a wide variety of applications, including simplifying fractions, finding divisors, and understanding divisibility rules.
Example: The prime factorization of 180 can be written as:
Once a number is expressed in terms of its prime factors, we can use these factors to find the HCF and LCM of multiple numbers. For instance, given two numbers, we can compare their prime factors to determine their highest common factor or least common multiple.
Practice Problem: Use prime factorization to find the HCF and LCM of 72 and 120.
Revisiting Irrational Numbers
Irrational numbers are numbers that cannot be expressed as a simple fraction of two integers. They have non-terminating, non-recurring decimal expansions, which means their decimal representation never ends and never repeats a pattern. Examples of irrational numbers include ,
,
, and
. Unlike rational numbers, irrational numbers cannot be precisely represented by a finite or repeating decimal.
One of the most famous irrational numbers is , which represents the ratio of the circumference of a circle to its diameter. Despite numerous attempts, no fraction can exactly equal
, and its decimal expansion goes on indefinitely without repeating.
In this chapter, students learn how to prove the irrationality of numbers like and
through contradiction. A common approach involves assuming the number is rational and showing that this assumption leads to a contradiction.
Proof that is irrational:
- Assume
is rational, i.e., it can be expressed as
where
and
have no common factors other than 1 (they are coprime).
- By squaring both sides, we get
, which implies that
.
- This equation shows that
is even, which means
must also be even.
- Let
(for some integer
), and substitute it back into the equation to get
or
, simplifying to
.
- This implies
is also even, which contradicts our assumption that
and
are coprime.
Thus, is irrational.
Similar methods can be used to prove that ,
, and other non-perfect square roots are irrational.
Example Problem: Prove that is irrational.
Summary of Key Points
- Real numbers encompass both rational and irrational numbers, forming the basis for representing all numbers on the number line.
- Euclid’s Division Lemma is useful in finding the HCF of two numbers by breaking down complex divisions into simple steps.
- The Fundamental Theorem of Arithmetic explains that every composite number has a unique prime factorization, which is foundational for operations involving HCF and LCM.
- Irrational numbers cannot be expressed as fractions and have non-terminating, non-repeating decimal expansions.
Real-Life Applications
- Real Numbers in Measurements: In science, engineering, and daily life, real numbers are used to measure distances, weights, temperatures, and other quantities with varying levels of precision. For instance, the dimensions of a building or the temperature in weather forecasting are often represented by real numbers.
- Euclid’s Division Lemma in Cryptography: This lemma forms the basis of several cryptographic algorithms used in encryption and data security. Algorithms involving modular arithmetic and prime factorization often rely on principles from Euclid’s Lemma.
- Irrational Numbers in Geometry: Irrational numbers like
are essential for calculations involving circles and spheres. For example, the circumference and area of a circle are calculated using
, an irrational number.
- Prime Factorization in Coding Theory: Prime factorization is crucial in coding theory and encryption, where security protocols depend on the difficulty of factorizing large composite numbers.
Practice Questions
Q1: Use Euclid’s Division Lemma to find the HCF of and
.
- Solution: Applying Euclid’s Division Lemma, we get:
- Since the remainder becomes zero, the last non-zero remainder is 9.
Answer: The HCF of 306 and 657 is 9.
Q2: Prove that is irrational.
- Solution: To prove
is irrational, we use a proof by contradiction.
- Assume that
is rational, i.e., it can be expressed as
, where
and
are coprime integers.
- Then,
, which implies
.
- Thus,
, which shows that
is divisible by 5, meaning
must also be divisible by 5.
- Let
for some integer
. Substituting, we get
or
, which simplifies to
.
- This means
is divisible by 5, so
must also be divisible by 5.
- Assume that
- Since both
and
are divisible by 5, this contradicts the assumption that
and
are coprime.
Answer: Therefore,is irrational.
Q3: Find the prime factorization of and use it to find the HCF and LCM with
.
- Solution:
- Prime Factorization:
- HCF:
- The common prime factors of 84 and 180 are
and
.
- Therefore,
.
- The common prime factors of 84 and 180 are
- LCM:
- For the LCM, we take the highest power of each prime factor appearing in either number:
,
,
, and
.
- Therefore,
.
- For the LCM, we take the highest power of each prime factor appearing in either number:
- Prime Factorization:
- Answer: The HCF is 12 and the LCM is 1260.
Q4: Express as a fraction.
- Solution: Let
(where
means the decimal repeats).
- Then,
.
- Subtracting these two equations, we get
, which simplifies to
.
- Dividing both sides by 9, we get
.
- Then,
- Answer:
.
Q5: Determine if has a terminating or non-terminating decimal expansion.
- Solution: To check if a fraction has a terminating decimal expansion, the denominator (in its simplest form) must have only 2 or 5 as its prime factors.
Here, , which has only 5 as a prime factor.
- Answer: Since the denominator has only 5 as a factor,
has a terminating decimal expansion.
Q6: Show that is irrational.
- Solution: To prove
is irrational, we use a proof by contradiction.
- Assume
is rational, i.e.,
for some integers
and
.
- Then,
.
- Since
and
are rational and irrational respectively, their difference
would also be irrational.
- Assume
- This contradicts our assumption that
is irrational.
Answer: Therefore,is irrational.
Q7: If the HCF of two numbers is and their product is
, find their LCM.
- Solution: The relationship between the HCF, LCM, and product of two numbers is given by:
Here,and the product of the two numbers is
.
- Substitute the values:
- Substitute the values:
- Answer: The LCM of the two numbers is 240.
Q8: Find the HCF of and
using the Fundamental Theorem of Arithmetic.
- Solution:
- Prime Factorization:
- HCF:
- The common prime factors of 54 and 24 are
and
.
- The lowest powers of these common factors are
and
.
- Therefore,
.
- The common prime factors of 54 and 24 are
- Prime Factorization:
- Answer: The HCF of 54 and 24 is 6.
FAQs
Rational numbers can be expressed as a fraction of two integers and have either terminating or repeating decimal expansions. Irrational numbers cannot be expressed as fractions and have non-terminating, non-recurring decimals.
By expressing each number in terms of its prime factors, we can identify the highest power of each prime factor present in the numbers. Multiplying these factors gives the LCM.
Certain square roots cannot be expressed as a fraction because their decimal expansions are non-terminating and non-repeating. The proof often involves assuming the number is rational and reaching a contradiction.
Euclid’s Division Lemma allows us to systematically divide two numbers, using remainders to progressively reduce the numbers until we reach the HCF. This method is efficient and widely used in number theory.
Yes, imaginary numbers, like the square root of -1 (denoted as i), are not real numbers. They form part of the complex numbers when combined with real numbers.
Zero is the additive identity in real numbers, meaning any real number added to zero equals the number itself.
Yes, real numbers can be both positive and negative, including zero.
Rational numbers can be expressed as a fraction with both numerator and denominator as integers, and the denominator is not zero. Irrational numbers have non-repeating, non-terminating decimals.
A real number can be any rational or irrational number. It includes all the numbers on the number line.



 , which implies that
, which implies that 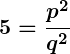 .
.






Get Social