Hey there, math whizzes! 📐 If numbers and equations have ever left you scratching your head, you’ve come to the right place. We’ve rounded up all the questions you might have and explained them in a way that’s easy to understand. Whether you’re grappling with the basics or the more challenging problems, this page is your ultimate guide to mastering Math in 10th grade. Let’s dive in and make those formulas and concepts as clear as day!
All MAths FAQs
To prove similarity, use the AA, SSS, or SAS criterion:
.
.
.
Similar triangles are used in:
- Indirect measurement techniques (e.g., finding heights of buildings).
- Map scaling and architectural designs.
In a right-angled triangle, one angle measures , and the Pythagoras Theorem holds:
.
The sum of the interior angles of a triangle is always .
The sum is derived by pairing terms of the sequence in reverse order, resulting in a simplified formula.
It helps in solving problems involving large sequences without manually adding all terms.
The nth term formula is derived from the general property of AP, where each term is the sum of the first term and a multiple of the common difference.
The nth term formula helps to calculate specific terms in a sequence without listing all preceding terms.
It is the formula used to find any term in the sequence: .
The common difference () is the fixed value obtained by subtracting any term from the next term.
An AP is a sequence of numbers where the difference between consecutive terms is constant.
Complex roots are non-real roots that exist in pairs and are conjugates of each other (e.g., and
)
Calculate the discriminant and use its value to identify the root type.
: Two distinct real roots.
: One repeated real root.
: Two complex roots.
The discriminant () determines the nature of the roots of a quadratic equation.
Use other methods like the quadratic formula or completing the square.
Factorisation works best when the quadratic equation can be split into integer factors easily.
Factorisation rewrites a quadratic equation as a product of two linear factors to find the variable’s value
Quadratic equations are used in physics, geometry, economics, engineering, and optimization problems.
The discriminant () determines if roots are real, repeated, or complex.
Factorization, completing the square, quadratic formula, and graphical method.
A polynomial equation of degree two, expressed as , where
.
If the equations represent parallel lines, there is no solution. If they represent the same line, there are infinitely many solutions. This can be determined by comparing the ratios of the coefficients.
Substitute the obtained values of x and y back into the original equations to ensure both equations are satisfied.
Yes, the elimination method is more efficient when the coefficients of one variable are already aligned or can be easily manipulated to align, allowing for quick elimination.
The substitution method is preferable when one equation is easily solvable for one variable, making substitution straightforward.
The steps are:
- Multiply one or both equations to align coefficients of one variable.
- Add or subtract the equations to eliminate that variable.
- Solve the resulting single-variable equation.
- Substitute the found value into one of the original equations to find the other variable.
The elimination method focuses on eliminating one variable by adding or subtracting equations, whereas the substitution method involves expressing one variable in terms of the other and substituting it into the second equation.
In the substitution method:
- Solve one of the equations for one variable in terms of the other.
- Substitute this expression into the second equation.
- Solve the resulting single-variable equation.
- Use the obtained value to find the other variable
The primary algebraic methods for solving a pair of linear equations are:
- Substitution Method: Solve one equation for one variable and substitute this expression into the other equation.
- Elimination Method: Add or subtract equations to eliminate one variable, simplifying the system to a single-variable equation.
The graphical method can be imprecise when finding exact values, especially if the point of intersection is not on grid lines. It also becomes less practical when dealing with more complex systems or when precise solutions are required.
Yes, by comparing the ratios of the coefficients ,
, and
, we can determine the type of solution:
- If
, the lines intersect and there is a unique solution.
- If
, the lines are coincident and there are infinitely many solutions.
- If
, the lines are parallel and there is no solution.
If the equations have different slopes, it means the lines will intersect at a single point. Therefore, the system of equations will have a unique solution.
Infinitely many solutions occur when the two lines overlap completely, or in other words, they are coincident. This means every point on the line satisfies both equations, so there are infinitely many solutions.
A unique solution exists when the lines represented by the equations intersect at exactly one point. This means there is one specific pair of values for and
that satisfies both equations.
If two lines are parallel, it means that they will never intersect, indicating that there is no common solution to the equations. In this case, the equations are said to be an “inconsistent pair” and have no solution.
In the graphical method, the point of intersection represents the solution to the pair of equations. The coordinates of the intersection point satisfy both equations simultaneously.
The graphical method involves plotting each equation on a graph as a line and finding the point(s) of intersection. The coordinates of the intersection point represent the solution to the equations. If the lines intersect at a single point, there is a unique solution. If they are parallel, there is no solution, and if they coincide, there are infinitely many solutions.
A polynomial of degree 4 can have up to four real zeros.
Yes, a cubic polynomial can have one, two, or three real zeros, depending on how it intersects the x-axis.
If the quadratic polynomial’s discriminant is less than zero, the polynomial has no real roots, so the parabola does not intersect the x-axis.
A polynomial of degree 2 (quadratic polynomial) can have up to two real zeros.
This concept is widely used in algebra, calculus, and even fields like physics and engineering. For example, in circuit analysis, certain electrical parameters can be modeled using polynomial equations, and understanding the relationships between zeroes and coefficients can help solve complex problems efficiently.
For higher-degree polynomials (beyond cubic), similar relationships exist. The sum of zeroes, the sum of products of zeroes taken two at a time, and so on, can be related to the coefficients. However, the exact relationships depend on the polynomial’s degree and are more complex as the degree increases.
Yes, knowing the zeroes and their relationships with the coefficients allows us to construct polynomials. For example, if the zeroes of a quadratic polynomial are given as and
, we can write it as:
Expanding this will provide a polynomial with the desired zeroes.
This relationship allows us to determine properties of a polynomial without fully solving it. It is useful in factoring polynomials, solving equations, and understanding the behavior of polynomial functions in graphing and analysis.
For a linear polynomial , the zero is:
Yes, in a cubic polynomial , the sum of the products of zeroes taken two at a time is:
For a cubic polynomial , the product of the zeroes
,
, and
is given by:
For a cubic polynomial , if
,
, and
are the zeroes, then:
This is the sum of zeroes expressed in terms of the coefficients of and
.
For a quadratic polynomial , if
and
are the zeroes, then:
and
where represents the sum of zeroes, and
represents the product of zeroes.
No, polynomials only include terms with non-negative integer exponents.
The zero polynomial has no terms, so it doesn’t have the highest power. Hence, its degree is considered undefined.
The degree is the highest power of the variable present in the polynomial. For example, in , the degree is 3.
A polynomial consists only of non-negative integer powers of a variable and real-number coefficients, making it a specific type of algebraic expression.
Yes, if a number is a perfect square, its square root is rational (e.g., ).
The result is always irrational, as shown in examples like .
The square root of a prime number cannot be expressed as a fraction, so it’s irrational. We use proof by contradiction and Theorem 1 to prove this.
Prime factorization allows us to identify the common factors for HCF and all factors for LCM.
The uniqueness comes from the fact that no two different sets of prime numbers can be multiplied to produce the same composite number.
The theorem states that every composite number can be uniquely factorized as a product of prime numbers, apart from the order of factors.
Rational numbers can be expressed as a fraction of two integers and have either terminating or repeating decimal expansions. Irrational numbers cannot be expressed as fractions and have non-terminating, non-recurring decimals.
By expressing each number in terms of its prime factors, we can identify the highest power of each prime factor present in the numbers. Multiplying these factors gives the LCM.
Certain square roots cannot be expressed as a fraction because their decimal expansions are non-terminating and non-repeating. The proof often involves assuming the number is rational and reaching a contradiction.
Euclid’s Division Lemma allows us to systematically divide two numbers, using remainders to progressively reduce the numbers until we reach the HCF. This method is efficient and widely used in number theory.
Sets can be represented in statement form, roster form, or set-builder form, depending on how their elements are defined.
A subset includes all elements of another set, including possibly being the same set, while a proper subset includes all elements but is not identical to the set.
The Cartesian product of two sets and
, denoted as
, is the set of all ordered pairs where the first element is from
and the second element is from
.
Sets are used in various fields like data science, logic, computer science, database management, probability, and statistics. For example, sets are used to group data, perform operations on databases, and calculate probabilities in statistical models.
The union of two sets includes all elements that are in either of the sets or in both. It is denoted by .
Some common types of sets are finite sets, infinite sets, empty sets (null sets), universal sets, power sets, subsets, and equal sets.
A set is a collection of distinct and well-defined objects, called elements. These elements can be anything from numbers to letters or even other sets.
Yes, imaginary numbers, like the square root of -1 (denoted as i), are not real numbers. They form part of the complex numbers when combined with real numbers.
Zero is the additive identity in real numbers, meaning any real number added to zero equals the number itself.
Yes, real numbers can be both positive and negative, including zero.
Rational numbers can be expressed as a fraction with both numerator and denominator as integers, and the denominator is not zero. Irrational numbers have non-repeating, non-terminating decimals.
A real number can be any rational or irrational number. It includes all the numbers on the number line.
Yes, mensuration formulas can be extended to irregular shapes using advanced mathematical techniques like calculus, particularly for integrating areas and volumes.
The volume of a 3D object is the space it occupies, measured in cubic units, while the surface area is the total area covered by the surface of the object, measured in square units.
The area of a circle can be calculated using the formula , where “r” is the radius of the circle.
Mensuration is vital for practical applications in fields like engineering, construction, and daily life tasks such as calculating space in home projects or material requirements.
Mensuration is the branch of mathematics that deals with the measurement of various parameters of geometric figures, including area, volume, and perimeter.
It is used in various practical fields like construction, navigation, and physics to calculate distances and verify measurements.
No, Pythagoras Theorem is specifically applicable only to right-angled triangles.
The theorem can be proved by equating the area of the square on the hypotenuse with the sum of the areas of the squares on the other two sides.
Pythagoras Theorem describes the relationship between the sides of a right-angled triangle, stating that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Complementary events are two outcomes of an event that sum to a probability of 1, such as passing or failing a test.
No, probability values range from 0 to 1.
A common example is tossing a coin, where the probability of getting heads is 0.5.
Calculate probability using the formula P(E)=(Total number of outcomes)/(Number of favorable outcomes).
Probability measures the likelihood of an event occurring, ranging from 0 (impossible) to 1 (certain).
For two functions, f and g, the quotient rule states that the derivative of their quotient is
The chain rule is used to find the derivative of composite functions. It multiplies the derivative of the outer function by the derivative of the inner function.
Trigonometric functions such as sine and cosine have specific derivatives: sin(x) differentiates to cos(x), and cos(x) differentiates to −sin(x).
The power rule states that the derivative of is
Deeksha Learning continuously updates its content to align with the latest educational standards and real-world applications. They incorporate new teaching methods and technologies to ensure the material is engaging, effective, and comprehensive.
Mathematics opens the door to numerous careers in engineering, economics, data science, actuarial science, academic research, and more. Proficiency in math is also highly valued in fields like finance, consulting, and technology.
Yes, with discipline and access to the right resources, students can self-teach mathematics. Platforms like Deeksha Learning provide comprehensive materials that students can use at their own pace to build and enhance their mathematical knowledge.
Many students find mathematics challenging due to a lack of foundational understanding, math anxiety, or previous negative experiences with the subject. Personalized learning approaches, like those offered by Deeksha Learning, can help overcome these barriers.
Deeksha Learning offers a range of interactive and engaging resources that simplify complex concepts and provide extensive practice in a structured manner. Their materials cater to different learning styles and help students grasp foundational concepts and advanced topics effectively.
Basic math concepts like counting and number recognition can be introduced as early as preschool. As children grow, more complex topics can be gradually introduced to align with their cognitive development and curiosity.
Mathematics helps in managing budgets, home improvement projects, cooking, and understanding data in the news. It fosters critical thinking and decision-making skills that are vital in everyday choices.
Effective strategies include practicing regularly, understanding the concepts rather than memorizing procedures, and applying mathematics to real-life situations to better understand its usage. Additionally, seeking help when needed and using educational resources like Deeksha Learning can be very beneficial.
Parents can help by encouraging a positive attitude towards mathematics, providing a quiet study space, and ensuring their child practices regularly. Engaging in games and activities that require mathematical thinking, like puzzles or building blocks, can also enhance a child’s learning.
Mathematics is crucial because it is the foundation of sciences and technology. It teaches problem-solving skills, logical reasoning, and the ability to think in abstract ways. Mathematics is used in every aspect of life, including finance, engineering, and the social sciences.
They are used to indicate positions in races, ranks in classes, floors in buildings, and places in lines.
Yes, typically, ordinal numbers are written with the numeral followed by the suffix (st, nd, rd, th), such as 1st, 2nd, 3rd, and 4th.
The ordinal number for 25 is “Twenty-Fifth” (25th).
Nominal numbers are used to name or identify objects, such as vehicle registration numbers and postal codes.
Sure! “Ram finished first in his class,” and “Sarita was the third girl in line.”
Ordinal numbers indicate position or order (e.g., 1st, 2nd, 3rd), while cardinal numbers indicate quantity (e.g., 1, 2, 3).
Ordinal numbers are numbers that indicate the position or rank of something in a list, such as 1st, 2nd, 3rd, etc.
Congruence can help in solving problems involving shapes and structures in geometry, ensuring designs are accurate and matching parts fit together perfectly.
CPCT stands for “Corresponding Parts of Congruent Triangles”
The main rules are SSS (Side-Side-Side), SAS (Side-Angle-Side), ASA (Angle-Side-Angle), AAS (Angle-Angle-Side), and RHS (Right angle-Hypotenuse-Side).
Two triangles are congruent if their corresponding sides and angles are equal, meaning they have the same shape and size.
Rational numbers can be expressed as fractions with non-zero denominators, while irrational numbers cannot be written as simple fractions and have endless, non-repeating decimals.
Rational numbers can be positive or negative. Positive if both numerator and denominator have the same sign, negative if they have opposite signs.
A number is rational if it can be written as p/q with q≠0 and can be simplified to a decimal form.
Yes, zero is a rational number because it can be expressed as 0/1.
A rational number is a number that can be expressed as a fraction p/q, where q is not zero.
The area of a triangle is measured in square units, such as square meters (m²) or square centimeters (cm²).
If two sides and the included angle are known, the area can be found using ½ b c sinA, where A is the included angle, and b and c are the sides.
Heron’s formula calculates the area of a triangle when the lengths of all three sides are known. It is , where s is the semi-perimeter of the triangle.
Yes, the formula applies to all types of triangles, including scalene, isosceles, and equilateral triangles.
The basic formula to find the area of a triangle is
The formula to convert centimeters to inches is:
inches = cm × 0.393701
Knowing how to convert inches to centimeters is important for understanding and comparing measurements between the Imperial and Metric systems. This is especially useful in fields like science, engineering, construction, and international trade, where different measurement systems are used.
To use an online inches to centimeters converter, simply enter the number of inches you want to convert, and the tool will automatically calculate and display the equivalent value in centimeters.
The formula to convert inches to centimeters is:
Cm = inches × 2.54
To convert centimeters to inches, multiply the number of centimeters by 0.393701. For example, to convert 10 centimeters to inches:
10 cm × 0.393701 inches/cm = 3.93701 inches
There are 2.54 centimeters in one inch.
To convert inches to centimeters, multiply the number of inches by 2.54. For example, to convert 10 inches to centimeters:
10 inches × 2.54 cm/inch = 25.4 cm
Double angle identities express trigonometric functions of double angles:
Sum and difference identities are used to find the sine and cosine of the sum or difference of two angles:
Periodicity identities allow shifting angles by , etc.:
Reciprocal identities relate trigonometric functions to their reciprocals:
The basic trigonometric functions are:
The largest number typically written with Roman numerals is 3,999, which is MMMCMXCIX. Larger numbers are usually written using a bar over the numeral, indicating multiplication by 1,000.
100 is written as C in Roman numerals.
The Roman numeral system does not have a symbol for zero. The concept of zero was introduced later by Indian mathematicians and was not part of the Roman numeral system.
Roman numerals are used for various purposes today, such as in clock faces, book chapter titles, movie sequels, and to denote significant events or dates like the year of construction on buildings.
Roman numerals are a number system that originated in ancient Rome and are used throughout Europe until the late Middle Ages. They use combinations of letters from the Latin alphabet (I, V, X, L, C, D, and M) to represent numbers.
Percentages are preferred because they provide a common base (100), making it easier to compare different quantities directly.
Percentages are used in various real-life situations such as calculating discounts, interest rates, grades, statistics, and comparing data.
Percentages standardize different quantities for comparison. For instance, comparing test scores as percentages rather than raw marks can show performance more clearly.
To calculate a percentage, divide the part by the total and then multiply by 100.
Percentage =( Part / Total )×100
A percentage is a way of expressing a number as a fraction of 100. It is denoted by the symbol %. For example, 50% means 50 out of 100.
Quantum numbers are crucial because they provide a unique address for each electron in an atom, defining its energy, position, and behavior. They help predict and explain the arrangement of electrons in atoms and the resulting chemical properties.
The spin quantum number (ms) describes the intrinsic spin of the electron within an orbital. It can have one of two values: +1/2 (spin up) or -1/2 (spin down).
The magnetic quantum number (ml) describes the orientation of an orbital in space relative to the other orbitals. Its values range from -l to +l. For instance, if l=1, ml can be -1, 0, or 1.
The azimuthal quantum number (l), also known as the angular or orbital quantum number, defines the subshell and shape of the orbital. It ranges from 0 to n-1. For example, for n=3, l can be 0, 1, or 2.
The principal quantum number (n) indicates the main energy level or shell of an electron within an atom. It can be any positive integer (1, 2, 3,…).
There are four quantum numbers:
- Principal quantum number (n)
- Azimuthal quantum number (l)
- Magnetic quantum number (ml)
- Spin quantum number (ms)
Quantum numbers are a set of values that describe the position and energy of an electron in an atom. They define the properties of atomic orbitals and the electrons in those orbitals.
Latest Maths Concepts Covered
- Criteria for Similarity of Triangles
- Graphical Method of Solution of a Pair of Linear Equations
- Geometrical Meaning of the Zeroes of a Polynomial
- Similarity of Triangles
- Introduction to Triangles
- Sum of First n Terms of an AP
- nth Term of an AP
- Introduction to Arithmetic Progressions
- Solution of a Quadratic Equation by Factorisation
- Introduction to Quadratic Equations
- Algebraic Methods of Solving a Pair of Linear Equations
- Pair of Linear Equations in Two Variables
- Relationship between Zeroes and Coefficients of a Polynomial
- Introduction to Polynomials
- Revisiting Irrational Numbers
- The Fundamental Theorem of Arithmetic
- Sets
- Real Numbers
- Pythagoras Theorem
- Probability
- Mensuration
- Rational Numbers
- Congruence of Triangles
- Differentiation Formulas
- Maths FAQs
- Ordinal Numbers
- Area of Triangle
- Trigonometry Formulas
- Roman Numerals
- Percentage
- Inches to Centimeters(cm) Converter
Related Topics
- Differentiation Formulas
- Probability
- Rational Numbers
- Area of Triangle
- Pythagoras Theorem
- Pair of Linear Equations in Two Variables
- Introduction to Quadratic Equations
- Algebraic Methods of Solving a Pair of Linear Equations
- The Fundamental Theorem of Arithmetic
- Percentage
- nth Term of an AP
- Solution of a Quadratic Equation by Factorisation
- Similarity of Triangles
- Inches to Centimeters(cm) Converter
- Introduction to Arithmetic Progressions



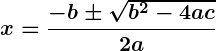
 , the lines intersect and there is a unique solution.
, the lines intersect and there is a unique solution.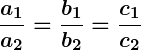 , the lines are coincident and there are infinitely many solutions.
, the lines are coincident and there are infinitely many solutions.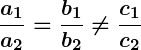 , the lines are parallel and there is no solution.
, the lines are parallel and there is no solution.








Get Social