Introduction
Linear equations in two variables are fundamental in algebra, with applications across mathematics and real-life scenarios. Solving these equations algebraically allows us to find exact solutions without relying on graphs. Two widely used algebraic methods are:
- Substitution Method
- Elimination Method
Substitution Method
The Substitution Method is based on isolating one variable in one of the equations and substituting it into the other equation to solve for the second variable.
Steps to Solve Using Substitution
- Isolate One Variable: Choose one equation and solve for one variable (either
or
) in terms of the other.
- Substitute: Replace the expression of the isolated variable into the second equation. This will result in a single-variable equation.
- Solve the Single-Variable Equation: Solve for the variable.
- Back-Substitute: Substitute the solved value into the equation from Step 1 to find the value of the other variable.
- Verify: Substitute both values into the original equations to ensure correctness.
Examples for Substitution Method
Example 1: Solve the Pair of Equations
and
Solution:
- Solve the first equation for
:
- Substitute
into the second equation:
- Simplify and solve for
:
- Substitute
into
:
Thus, the solution is:
Example 2: Solve the Pair of Fractional Equations
and
Solution:
- Solve the first equation for
:
- Substitute
into the second equation:
- Simplify:
Combine terms to solve for(step-by-step calculations will depend on simplifying fractions).
Elimination Method
The Elimination Method eliminates one variable by adding or subtracting the equations, allowing us to solve for the other variable.
Steps to Solve Using Elimination
- Align the Equations: Write both equations in standard form,
.
- Equalize Coefficients: Multiply one or both equations so the coefficients of one variable become equal.
- Eliminate One Variable: Add or subtract the equations to eliminate one variable.
- Solve for the Remaining Variable: Solve the resulting single-variable equation.
- Substitute and Solve: Substitute the value of the solved variable into one of the original equations to find the value of the other variable.
- Verify: Check the solution in both original equations.
Examples for Elimination Method
Example 1: Solve the Pair of Equations
and
Solution:
- Multiply the equations to align coefficients of
:
- Multiply the first equation by
and the second equation by
:
- Multiply the first equation by
- Subtract Equation 4 from Equation 3:
- Substitute
into the first equation:
Thus, the solution is:
Example 2: Solve the Pair of Fractional Equations
and
Solution:
- Eliminate fractions by multiplying through by the LCM:
- For the first equation, multiply by 12:
- For the second equation, multiply by 10:
- For the first equation, multiply by 12:
- Align coefficients of
by multiplying:
- Multiply the first equation by 2 and the second equation by 3:
- Multiply the first equation by 2 and the second equation by 3:
- Add Equations 3 and 4 to eliminate
:
- Substitute
into
:
Thus, the solution is:
Key Takeaways
- The Substitution Method is ideal for equations where isolating one variable is simple.
- The Elimination Method is efficient when coefficients are aligned or can be easily adjusted.
- Mastering both methods ensures accuracy in solving any pair of linear equations.
FAQs
If the equations represent parallel lines, there is no solution. If they represent the same line, there are infinitely many solutions. This can be determined by comparing the ratios of the coefficients.
Substitute the obtained values of x and y back into the original equations to ensure both equations are satisfied.
Yes, the elimination method is more efficient when the coefficients of one variable are already aligned or can be easily manipulated to align, allowing for quick elimination.
The substitution method is preferable when one equation is easily solvable for one variable, making substitution straightforward.
The steps are:
- Multiply one or both equations to align coefficients of one variable.
- Add or subtract the equations to eliminate that variable.
- Solve the resulting single-variable equation.
- Substitute the found value into one of the original equations to find the other variable.
The elimination method focuses on eliminating one variable by adding or subtracting equations, whereas the substitution method involves expressing one variable in terms of the other and substituting it into the second equation.
In the substitution method:
- Solve one of the equations for one variable in terms of the other.
- Substitute this expression into the second equation.
- Solve the resulting single-variable equation.
- Use the obtained value to find the other variable
The primary algebraic methods for solving a pair of linear equations are:
- Substitution Method: Solve one equation for one variable and substitute this expression into the other equation.
- Elimination Method: Add or subtract equations to eliminate one variable, simplifying the system to a single-variable equation.
Related Topics
- Real Numbers
- Sum of First n Terms of an AP
- Roman Numerals
- Mensuration
- Probability
- Maths FAQs
- Percentage
- Revisiting Irrational Numbers
- Congruence of Triangles
- Area of Triangle
- Graphical Method of Solution of a Pair of Linear Equations
- The Fundamental Theorem of Arithmetic
- Introduction to Arithmetic Progressions
- Rational Numbers
- nth Term of an AP



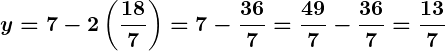
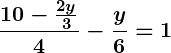










Get Social