Introduction
Refraction of light is a fundamental concept in optics, describing how light bends when it passes from one medium into another. Unlike reflection, where light bounces off a surface, refraction occurs when light travels from one transparent medium (such as air) to another (such as water or glass). This bending is caused by a change in the speed of light as it enters the new medium, which depends on the optical density of the mediums involved.
What is Refraction of Light?
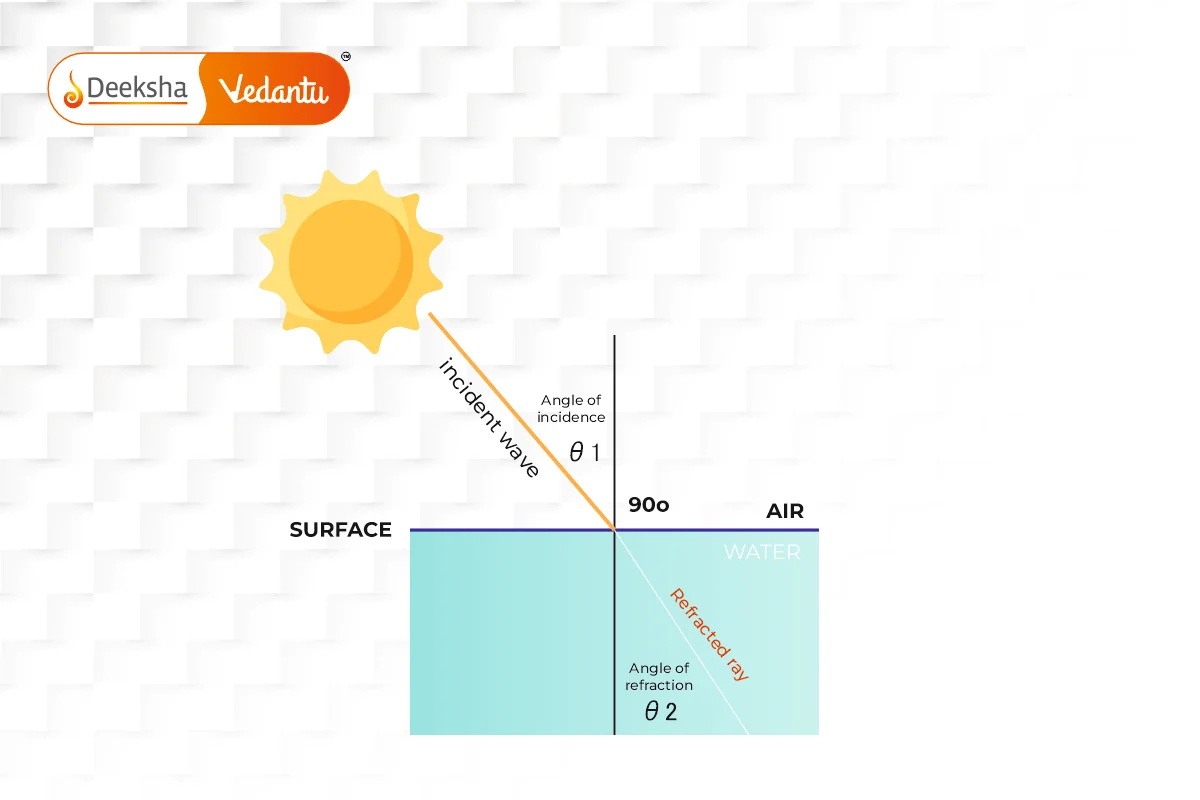
Refraction is the bending of light when it passes obliquely from one transparent medium to another. This bending occurs because the speed of light changes as it moves from one medium to another. The extent of refraction depends on the refractive indices of the two media.
For example, when a straw is placed in a glass of water, it appears bent or broken at the water’s surface. This is due to the refraction of light as it moves from air into water, making the submerged part of the straw appear to be at a different angle.
Laws of Refraction of Light
Refraction follows two important laws, known as Snell’s Laws of Refraction:
- First Law of Refraction: The incident ray, the refracted ray, and the normal to the surface of separation all lie in the same plane.
- Second Law of Refraction (Snell’s Law): The ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant for a given pair of media. This constant is the refractive index of the second medium with respect to the first medium.
Where:
is the angle of incidence,
is the angle of refraction, and
is the refractive index of the second medium with respect to the first.
Explanation of Snell’s Law:
- When light passes from a less dense medium (like air) to a more dense medium (like water), it slows down and bends towards the normal.
- When light passes from a more dense medium to a less dense medium, it speeds up and bends away from the normal.
Refractive Index
The refractive index of a medium is a measure of how much light slows down in that medium compared to its speed in a vacuum. It is denoted by n. The refractive index can be calculated as:
Where:
is the refractive index of the medium,
is the speed of light in a vacuum (
),
is the speed of light in the medium.
The higher the refractive index of a medium, the slower light travels through it.
Common Refractive Indices:
- Air: n=1.0003 (approximately 1)
- Water: n=1.33
- Glass: n=1.5
- Diamond: n=2.42
Refraction Through a Glass Slab
When light passes through a rectangular glass slab, it undergoes refraction at both air-glass and glass-air interfaces. Although the light rays bend at both surfaces, the overall direction of the ray remains unchanged. However, the emergent ray is displaced from its original path. This lateral shift is called the lateral displacement of the emergent ray.

In this case:
- Incident Ray (PQ): The light ray that approaches the glass slab from air at point Q.
- Normal (N): The perpendicular line to the surface of the glass at point Q.
- Angle of Incidence (i): The angle (
) between the incident ray and the normal.
- Refraction at Q: As the light enters the glass slab, it bends towards the normal (from N to N’), indicating the change in speed due to the denser medium (glass).
- Refracted Ray (EF): The light ray that travels through the glass slab.
- Angle of Refraction (r): The angle between the refracted ray and the normal inside the glass.
- Emergence at R: The refracted ray exits the glass at point R, bending away from the normal (N’).
- Angle of Emergence (e): The angle (
) between the emergent ray and the normal outside the glass.
- Emergent Ray (RS): The light ray emerging out of the glass, parallel to the incident ray but displaced laterally (MM’).
The diagram shows that the emergent ray is parallel to the incident ray but shifted by a lateral displacement (d). This illustrates the phenomenon of refraction and the principle that light bends towards the normal when entering a denser medium and away from the normal when leaving it.
Refraction in Real Life
- Bent Appearance of Objects in Water: Objects submerged in water, such as a pencil or a coin, appear bent or shifted from their original position due to the refraction of light.
- Mirages: On hot days, a distant road may appear to have water on it due to the refraction of light caused by layers of hot and cool air.
- Lenses in Glasses and Cameras: Lenses use the principle of refraction to focus light and form clear images.
Critical Angle and Total Internal Reflection
When light travels from a denser medium to a rarer medium (like from water to air), there is an angle called the critical angle beyond which the light no longer refracts but instead reflects entirely within the denser medium. This phenomenon is known as Total Internal Reflection.
- Critical Angle: The angle of incidence in the denser medium for which the angle of refraction is
.
- Total Internal Reflection: If the angle of incidence exceeds the critical angle, the light reflects back entirely into the denser medium, instead of refracting into the rarer medium.
Formula for Critical Angle (C):
Where:
is the critical angle,
is the refractive index of the denser medium with respect to the rarer medium.
Applications of Refraction of Light
- Lenses in Eyeglasses and Cameras: Lenses use refraction to focus light and correct vision defects or form clear images.
- Optical Fibers: Optical fibers rely on the principle of total internal reflection to transmit light signals over long distances with minimal loss.
- Prisms: Prisms use refraction to disperse white light into its component colors (the visible spectrum).
Practice Questions with Answers
Q1: Define refraction of light.
- Answer: Refraction of light is the bending of light rays as they pass obliquely from one medium to another, caused by a change in the speed of light in different media.
Q2: State Snell’s law of refraction.
- Answer: Snell’s law states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is a constant for a given pair of media:
Where is the refractive index.
Q3: Why does a pencil appear bent when partially submerged in water?
- Answer: The pencil appears bent because light rays from the part of the pencil submerged in water are refracted (bent) when they pass from water (denser medium) to air (rarer medium), making the pencil seem displaced at the water’s surface.
Q4: Calculate the refractive index of a medium if the speed of light in that medium is
- Answer:
Therefore, the refractive index of the medium is 1.5.
Q5: A ray of light enters a glass slab from air at an angle of incidence of . If the refractive index of glass is 1.5, calculate the angle of refraction.
- Answer: Using Snell’s law:
Given:,
- So,
Hence,
FAQs
The refractive index of air is almost equal to 1 because the speed of light in air is very close to its speed in a vacuum.
Total internal reflection is the phenomenon where light, traveling from a denser to a rarer medium, is completely reflected back into the denser medium when the angle of incidence exceeds the critical angle.
Light bends during refraction because it changes speed when it passes from one medium to another. The bending occurs due to the difference in optical densities of the two media.
The refractive index is the ratio of the speed of light in a vacuum to the speed of light in a given medium. It indicates how much light slows down in that medium.
Related Topics
- Dispersion Of White Light By A Glass Prism
- Factors On Which The Resistance Of A Conductor Depends
- Work, Energy and Power
- Magnet
- List of Physics Scientists and Their Inventions
- Electric Potential And Potential Difference
- Atmospheric Refraction
- Faraday’s Law
- P-N Junction
- Human Eye – Structure and Functioning
- Magnetic Field Due To A Current – Carrying Conductor
- Spherical Mirrors
- Acceleration
- Reflection Of Light
- Compound Microscope




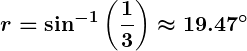








Get Social