Introduction
A real number is a zero of the polynomial
if
. The zeros of a polynomial are significant as they represent the points where the graph of the polynomial intersects the x-axis. In this section, we explore the geometrical representations of linear, quadratic, and cubic polynomials and the meaning of their zeros on a graph.
Graph of a Linear Polynomial
A linear polynomial is a polynomial of degree 1 and has the general form , where
. The graph of a linear polynomial is a straight line, and its zero represents the point at which this line intersects the x-axis. Since the x-axis is defined by
, the zero of the polynomial
is the solution to
.
- Finding the Zero:
To find the zero of, we solve the equation
. This gives us:
- Example:
- Consider
.
- Setting
, we get
.
- The zero is
.
- Consider
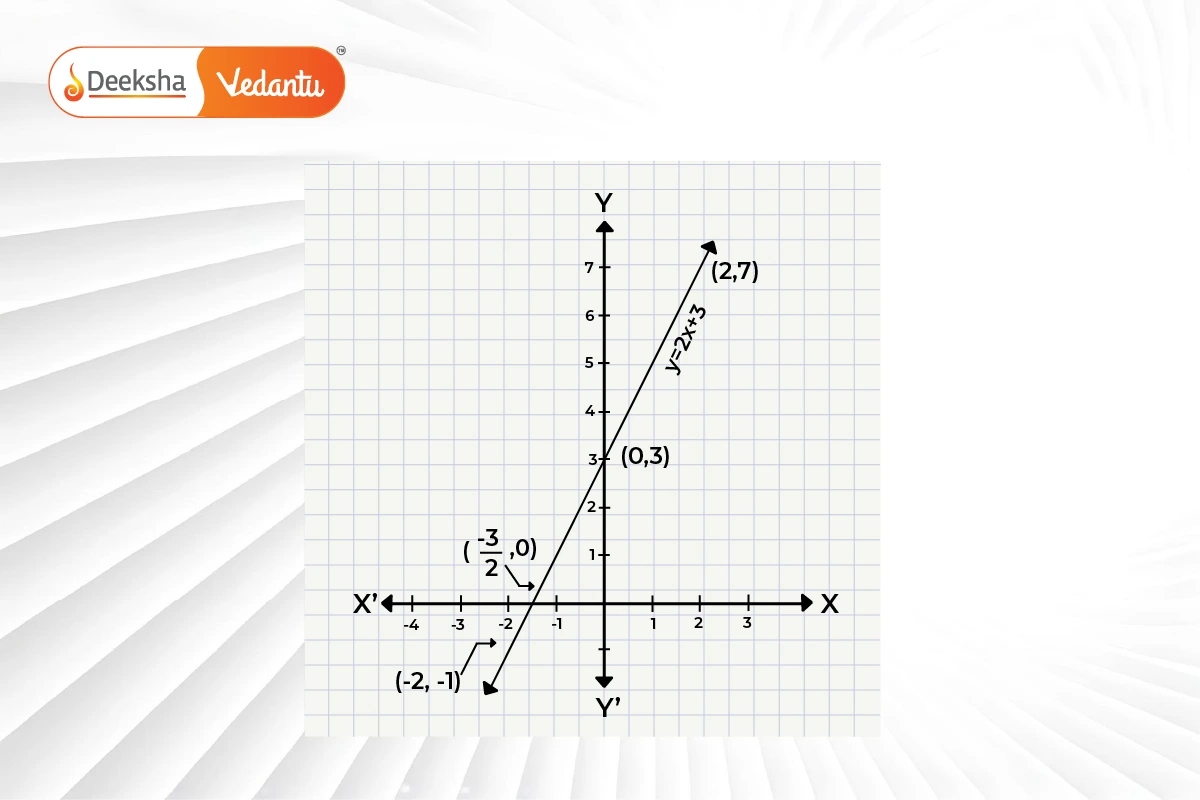
- Graphical Interpretation:
The graph ofpasses through points like
and
. It intersects the x-axis at
. Thus, the zero of the linear polynomial is where this line crosses the x-axis
Graph of a Quadratic Polynomial
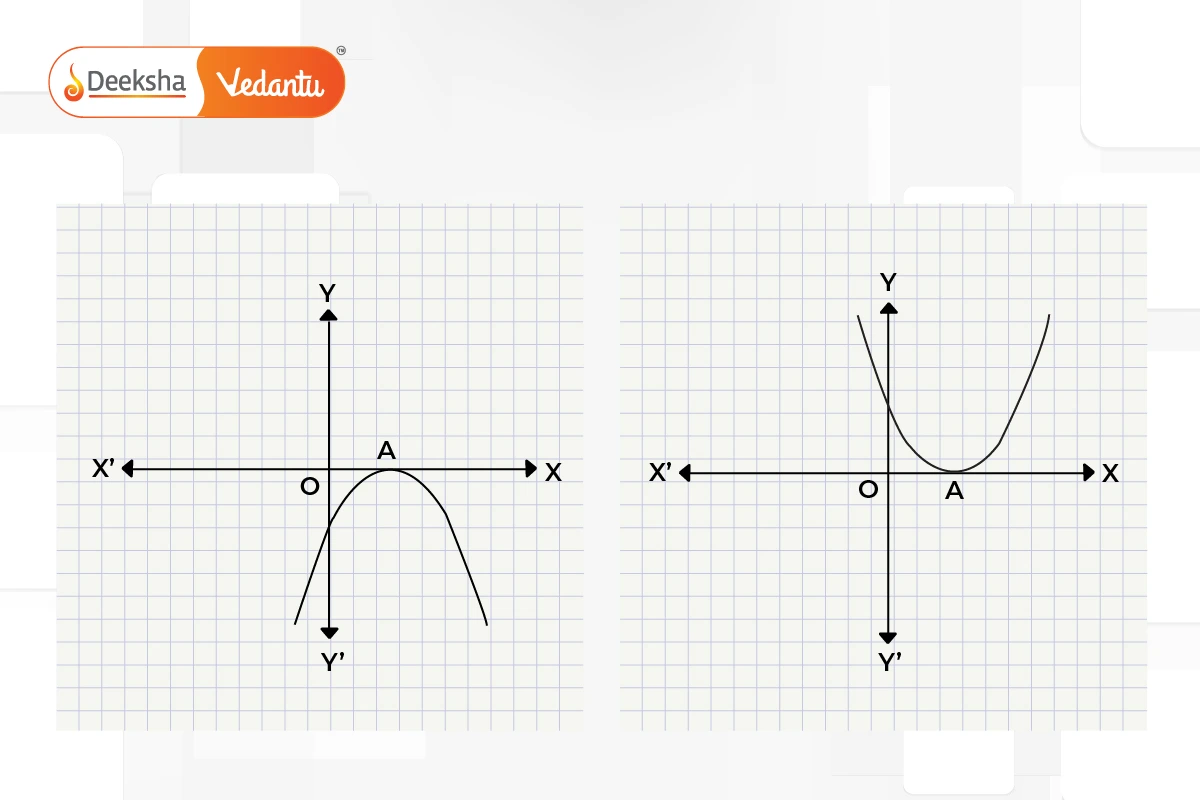
A quadratic polynomial is a polynomial of degree 2 and has the general form , where
. The graph of a quadratic polynomial is a parabola, which opens either upwards (if
) or downwards (if
). The points where this parabola intersects the x-axis are the zeros of the polynomial.
- Possible Cases for Zeros:
Depending on the discriminant, a quadratic polynomial can have:
- Two distinct real zeros if
.
- One real zero (repeated) if
.
- No real zeros if
.
- Two distinct real zeros if
- Example:
- Consider
.
- Solving
by factoring, we find
and
.
- These values represent the x-coordinates where the graph intersects the x-axis.
- Consider
- Graphical Representation:
The zeros of the polynomial correspond to the points where the parabola intersects the x-axis. The shape of the parabola and the nature of its zeros can vary, as described in the cases below.
Geometrical Meaning of Zeros for a Quadratic Polynomial – Detailed Cases
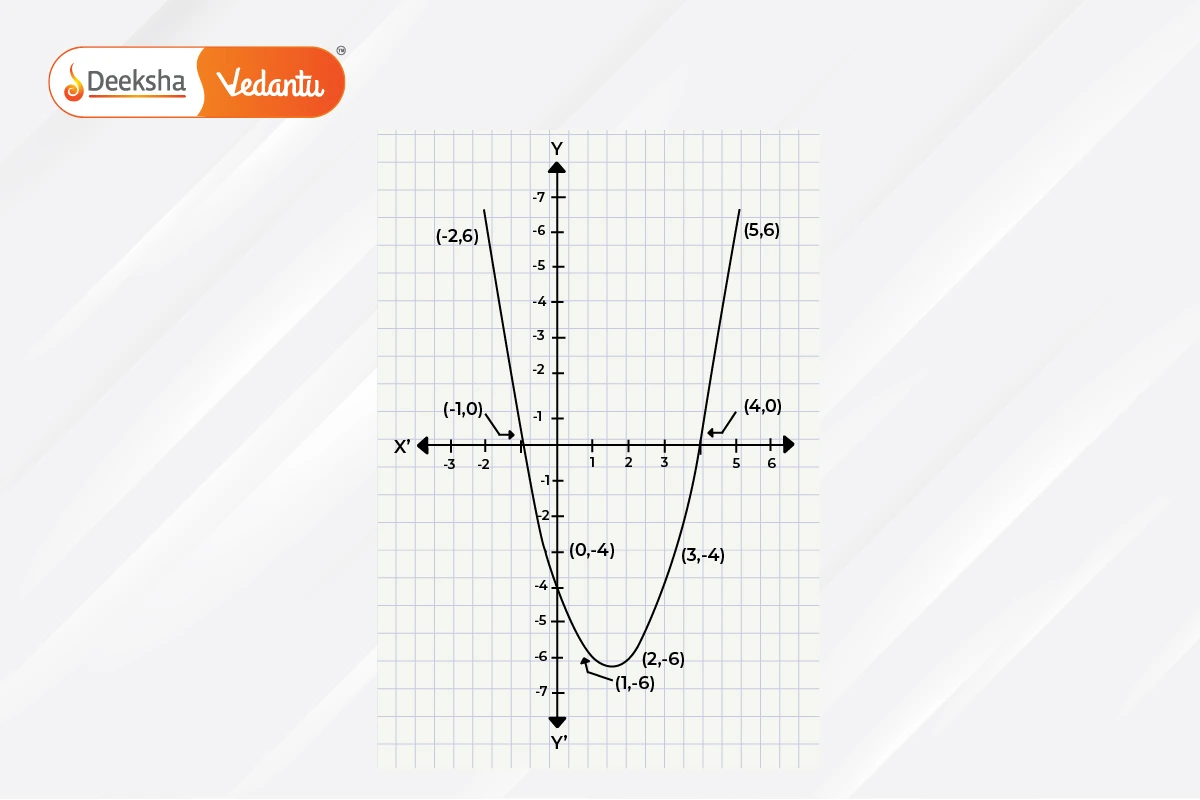
Case (i): Two Distinct Zeros
When a quadratic polynomial has two distinct zeros, the parabola intersects the x-axis at two different points, say and
. The x-coordinates of
and
are the zeros of the polynomial.
Example:
- For
, we find zeros at
and
.
- The graph intersects the x-axis at these two points, showing that the polynomial has two distinct real zeros.

Case (ii): One Zero (Repeated)
If the discriminant is zero (), the parabola touches the x-axis at only one point, meaning it has a single, repeated zero (or a double root). This is the point where the parabola just “touches” the x-axis without crossing it.
Example:
- For
, the polynomial has a zero at
.
- Graphically, this means the parabola touches the x-axis at
without intersecting it at any other point.
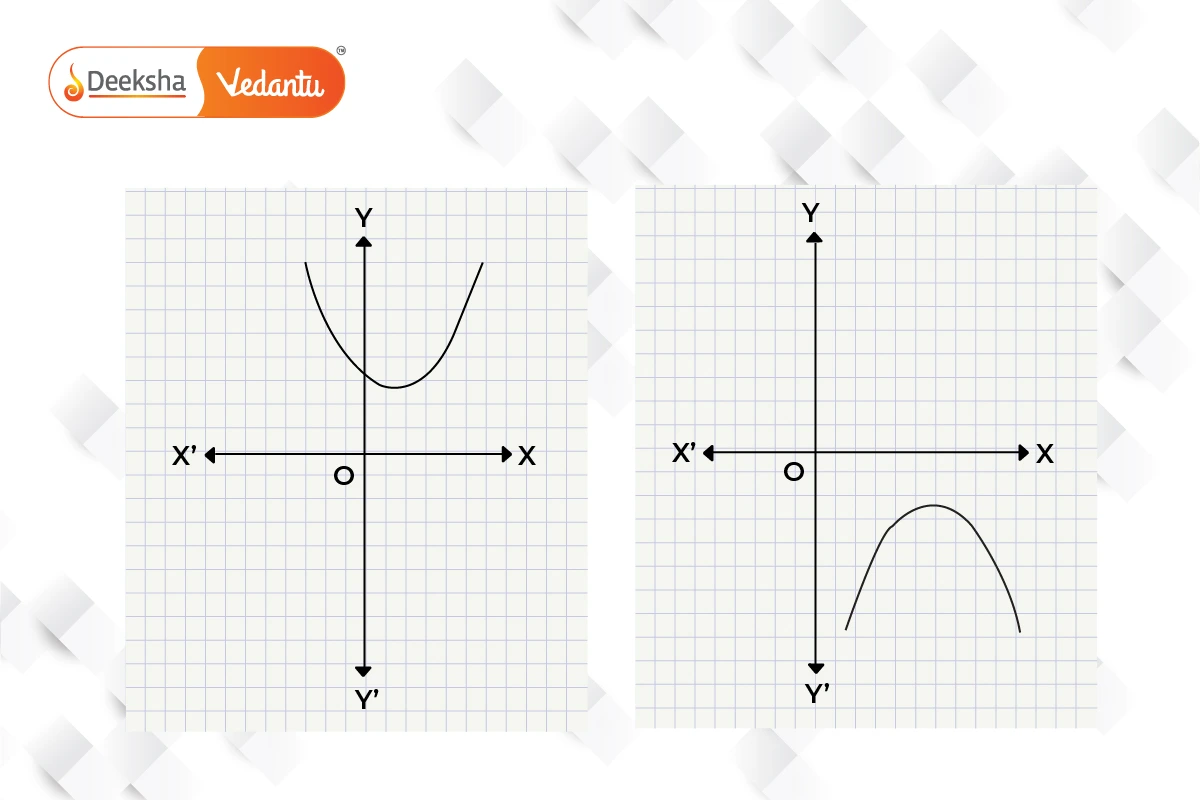
Case (iii): No Real Zeros
If the parabola is entirely above or below the x-axis (depending on the sign of ), it does not intersect the x-axis at any point. This situation occurs when the discriminant is negative (
), indicating no real solutions for
.
Example:
- For
, there are no real zeros, as the equation
has no real solutions.
- Graphically, the parabola lies above the x-axis (if
) or below it (if
).
Graph of a Cubic Polynomial
A cubic polynomial is a polynomial of degree 3 and has the general form , where
. The graph of a cubic polynomial has an S-shape and can intersect the x-axis up to three times, indicating up to three real zeros. Unlike quadratic polynomials, cubic polynomials are guaranteed to have at least one real zero due to the nature of cubic functions.
- Possible Cases for Zeros:
- A cubic polynomial can have one, two, or three real zeros.
- The exact number and nature of these zeros depend on the specific coefficients of the polynomial.
- Example:
- Consider
.
- We can factorize it as
.
- This gives the zeros
, meaning the graph intersects the x-axis at these points.
- Consider
- Graphical Interpretation:
- The graph of
intersects the x-axis at
,
, and
, illustrating that the polynomial has three real zeros.
- Other cubic polynomials may have fewer intersections with the x-axis, depending on their structure, but a cubic polynomial will always cross the x-axis at least once.
- The graph of

- Additional Examples:
- For
, there is only one zero at
.
- For
, the polynomial has zeros at
and
.
- For
General Observations on Polynomial Degrees and Zeros
- Degree and Maximum Zeros:
- A polynomial of degree
can have at most
real zeros.
- For instance, a quadratic polynomial (degree 2) has at most two zeros, while a cubic polynomial (degree 3) can have up to three zeros.
- A polynomial of degree
- Graph and Zeros Relationship:
- The zeros of a polynomial are the x-coordinates where its graph intersects the x-axis. This relationship helps in visualizing the polynomial and understanding its behavior graphically.
These observations form the foundation for understanding the behavior of polynomials and their intersections with the x-axis.
Example Problems
Example 1: Determine the number of zeros for the polynomial and describe their geometrical significance.
- Solution: Set
.
- Factorization:
.
- Zeros:
and
.
- Geometrically, these zeros are the x-coordinates where the graph of
intersects the x-axis.
- Factorization:
Example 2: Find the zeros of the cubic polynomial and explain their meaning.
- Solution: Set
.
- Factoring:
.
- Zeros:
.
- These zeros represent the points where the graph of
intersects the x-axis.
- Factoring:
Example 3: Determine the nature and number of zeros for the quadratic polynomial .
- Solution: Setting
results in
, which has no real solution.
- Therefore,
has no real zeros, and the graph does not intersect the x-axis.
- Therefore,
FAQs
A polynomial of degree 4 can have up to four real zeros.
Yes, a cubic polynomial can have one, two, or three real zeros, depending on how it intersects the x-axis.
If the quadratic polynomial’s discriminant is less than zero, the polynomial has no real roots, so the parabola does not intersect the x-axis.
A polynomial of degree 2 (quadratic polynomial) can have up to two real zeros.
Related Topics
- Probability
- Rational Numbers
- Ordinal Numbers
- Algebraic Methods of Solving a Pair of Linear Equations
- Introduction to Triangles
- nth Term of an AP
- Relationship between Zeroes and Coefficients of a Polynomial
- Real Numbers
- Solution of a Quadratic Equation by Factorisation
- Percentage
- Introduction to Quadratic Equations
- Graphical Method of Solution of a Pair of Linear Equations
- Similarity of Triangles
- Introduction to Arithmetic Progressions
- Maths FAQs



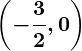 . Thus, the zero of the linear polynomial is where this line crosses the x-axis
. Thus, the zero of the linear polynomial is where this line crosses the x-axis





Get Social