Introduction to Trigonometric Ratios
Definition
Trigonometric ratios are mathematical relationships that connect the angles and sides of a right triangle. These ratios are derived from the geometric properties of right triangles and are used to define six primary trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent. Each ratio expresses the proportion between specific sides of the triangle relative to one of its acute angles, .
Significance
Trigonometric ratios are fundamental to the study of trigonometry, serving as the basis for solving a wide range of problems in mathematics and its applications:
- Problem-Solving in Geometry: They enable calculations of unknown sides and angles in triangles.
- Applications in Real Life: Trigonometric ratios are used in fields like engineering, navigation, physics, and astronomy.
- Foundation for Advanced Concepts: These ratios lay the groundwork for understanding trigonometric identities, equations, and functions.
Connection to Right Triangles
- Definition Relative to Acute Angles (
): In a right triangle:
- Opposite Side: The side directly opposite the angle
.
- Adjacent Side: The side next to the angle
(excluding the hypotenuse).
- Hypotenuse: The longest side of the triangle, opposite the right angle.
- Opposite Side: The side directly opposite the angle
- Trigonometric Ratios Relative to
:
- Universality Across Right Triangles: The trigonometric ratios depend only on the angle
and are independent of the size of the triangle. This property makes them applicable to all similar right triangles.
Definitions of Trigonometric Ratios
1. Sine ( ):
):
The ratio of the length of the opposite side to the length of the hypotenuse in a right triangle:
2. Cosine ( ):
):
The ratio of the length of the adjacent side to the length of the hypotenuse in a right triangle:
3. Tangent ( ):
):
The ratio of the length of the opposite side to the length of the adjacent side in a right triangle:
4. Cosecant ( ):
):
The reciprocal of , representing the ratio of the length of the hypotenuse to the length of the opposite side:
5. Secant ( ):
):
The reciprocal of , representing the ratio of the length of the hypotenuse to the length of the adjacent side:
6. Cotangent ( ):
):
The reciprocal of , representing the ratio of the length of the adjacent side to the length of the opposite side:
Key Observations
- Trigonometric ratios depend on the angle
and describe geometric relationships within a right triangle.
- Reciprocal relationships among trigonometric functions simplify complex calculations:
,
,
.
Relationship Between Trigonometric Ratios
Reciprocal Relationships
Trigonometric functions are interrelated through reciprocal identities, which express one function as the reciprocal of another. These are:
- Cosecant (
):
Reciprocal of:
- Secant (
):
Reciprocal of:
- Cotangent (
):
Reciprocal of:
Quotient Identities
Quotient identities establish relationships between ,
,
, and
:
- Tangent (
):
The ratio ofto
:
- Cotangent (
):
The ratio ofto
:
Key Observations
- Symmetry and Interdependence:
Trigonometric ratios are interdependent, simplifying calculations by reducing complex expressions to simpler forms. - Applications:
Reciprocal and quotient identities are widely used in:- Simplifying trigonometric expressions.
- Solving trigonometric equations.
- Establishing relationships in geometry and physics.
Applications of Trigonometric Ratios
1. In Geometry
Trigonometric ratios are essential for solving problems involving right triangles:
- Finding Unknown Sides:
Given one side and an angle, trigonometric ratios like
or
can be used to calculate the other sides.
- Example: If
and the hypotenuse is
, the opposite side is: Opposite
- Example: If
- Finding Unknown Angles:
When two sides of a right triangle are known, ratios likecan calculate the angle.
2. In Physics
Trigonometric ratios are critical for analyzing various physical phenomena:
- Forces and Motion:
Trigonometric ratios resolve forces into components along perpendicular directions (e.g., horizontal and vertical).- Example: A force
acting at an angle
has components:
- Example: A force
- Waves and Oscillations:
Trigonometric functions model periodic motion, such as sound waves and light waves:
Here,represents the oscillatory behavior.
- Projectile Motion:
Trigonometric ratios determine the range and height of a projectile:- Horizontal Range:
- Maximum Height:
- Horizontal Range:
3. In Real Life
Trigonometric ratios solve practical problems related to heights, distances, and angles:
- Height and Distance Problems:
- Example: To find the height of a tower using the angle of elevation and horizontal distance:
Rearranging:
- Example: To find the height of a tower using the angle of elevation and horizontal distance:
- Navigation and Surveying:
Trigonometry calculates distances and directions, especially in GPS and map-making. - Architecture and Construction:
Used to calculate slopes, angles, and dimensions in blueprints.
Example: Calculate the Height of a Building
Problem:
An observer standing 50 meters away from a building sees the top at an angle of elevation of . Find the height of the building.
Solution:
Using 
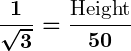
Related Topics
- The Fundamental Theorem of Arithmetic
- Solution of a Quadratic Equation by Factorisation
- Maths FAQs
- Ordinal Numbers
- Introduction to Quadratic Equations
- Probability
- Sets
- Congruence of Triangles
- Pythagoras Theorem
- Rational Numbers
- Similarity of Triangles
- Percentage
- Pair of Linear Equations in Two Variables
- Introduction to Polynomials
- Some applications Of Trigonometry




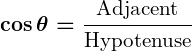

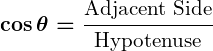


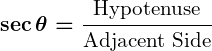

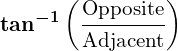 can calculate the angle.
can calculate the angle.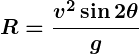
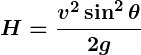









Get Social