Introduction to Trigonometric Identities
Definition
Trigonometric identities are equations that express relationships between trigonometric ratios such as ,
, and
. These identities hold true for all values of
where the trigonometric functions are defined (e.g.,
and
are undefined at
or
, respectively).
Importance
- Simplify Complex Expressions:
Trigonometric identities reduce the complexity of trigonometric expressions by converting them into simpler or equivalent forms. - Solve Trigonometric Equations:
They help isolate variables and find solutions to equations involving trigonometric functions. - Prove Mathematical Relationships:
Identities are used to verify equations or establish new relationships between trigonometric functions. - Applications in Geometry and Physics:
- In geometry, they simplify calculations involving angles and lengths.
- In physics, they are essential for analyzing oscillatory motion, wave behavior, and force components.
Key Idea
Trigonometric identities are universal, meaning they apply to all valid values of and are derived from fundamental geometric principles, such as the Pythagorean theorem.
Fundamental Trigonometric Identities
Pythagorean Identities
The Pythagorean identities are derived from the Pythagorean theorem applied to a right triangle. These identities form the foundation of many trigonometric calculations.
- First Pythagorean Identity:
- Second Pythagorean Identity:
Divide the first identity by:
- Third Pythagorean Identity:
Divide the first identity by:
Reciprocal Identities
Reciprocal identities express the relationships between trigonometric functions and their reciprocals.
- Cosecant (
):
- Secant (
):
- Cotangent (
):
Quotient Identities
Quotient identities define and
as ratios of
and
.
- Tangent (
):
- Cotangent (
):
Proving Trigonometric Identities
To prove a trigonometric identity, simplify one side of the equation to match the other by using algebraic operations and known trigonometric identities.
Example: Prove 
Solution:
- Start with the left-hand side (LHS) of the equation:
- Use the Pythagorean identity
:
- Simplify by canceling
:
- The right-hand side (RHS) matches the simplified LHS. Hence, the identity is proven:
.
Key Tips for Proving Identities
- Work on One Side at a Time:
Usually, simplify the more complex side of the equation. - Use Fundamental Identities:
Apply Pythagorean, reciprocal, and quotient identities as needed:, etc.
- Simplify Expressions Step-by-Step:
Factorize, expand, or rewrite terms to achieve equivalence.
Applications of Trigonometric Identities
Simplifying Expressions
Trigonometric identities simplify complex expressions by converting them into equivalent, simpler forms.
Example: Simplify
Solution:
- Recall the Pythagorean identity:
,
which implies.
- Substitute
for
in the denominator:
.
- Simplify:
.
The simplified expression is .
Solving Trigonometric Equations
Trigonometric identities are used to rewrite equations, making it easier to isolate the variable .
Example: Solve .
Solution:
- Use the Pythagorean identity
.
- Substitute
for
:
.
- Simplify:
.
This verifies the equation.
Geometry and Physics
Trigonometric identities are essential in analyzing angles and solving real-world problems, especially in geometry and physics.
- Wave Motion and Oscillations:
Trigonometric identities simplify equations involving wave behavior.
Example: For a wave modeled as, identities like
help calculate energy distribution.
- Optics and Mechanics:
In optics, trigonometric identities calculate angles of reflection, refraction, and light wave interference. - Analyzing Angles:
Identities determine unknown angles in structural design, navigation, and astronomy.
Special Trigonometric Identities
Angle Sum and Difference Identities
- Sine of Sum and Difference:
- Cosine of Sum and Difference:
- Tangent of Sum and Difference:
Double Angle Identities
- Sine of Double Angle:
- Cosine of Double Angle:
Alternate forms:
- Tangent of Double Angle:
Half-Angle Identities
- Sine of Half-Angle:
- Cosine of Half-Angle:
Applications of Special Trigonometric Identities
Simplifying Trigonometric Expressions
Trigonometric identities help reduce complex expressions to simpler forms, making calculations easier and more manageable.
Example: Rewrite in terms of
and
.
Solution:
- Recall the double-angle identity for sine:
- This identity is useful in simplifying expressions involving
.
For example, in the expression, substitute
and simplify further using
.
Applications:
- Used in deriving wave equations in physics.
- Simplifies problems in calculus, such as integration and differentiation involving trigonometric functions.
Solving Trigonometric Equations
Trigonometric identities are powerful tools for solving equations that would otherwise be difficult to handle.
Example: Solve .
Solution:
- Recall the double-angle identity for cosine:
- Substitute the given value:
- Simplify and solve for
:
- Take the square root:
- Solve for
within the required interval.
Applications:
- Used in geometry to calculate unknown angles.
- Essential in physics to analyze harmonic motion or oscillations.
Analyzing Periodic Phenomena
Trigonometric identities play a crucial role in studying periodic behaviors in various fields, especially physics and engineering.
Applications in Physics:
- Wave Mechanics:
- Functions like
and
describe oscillatory behavior in waves.
- Example: The displacement of a pendulum or the vibration of a string is modeled using
and
.
- Functions like
- Oscillations:
- In simple harmonic motion (SHM), the position, velocity, and acceleration are described using trigonometric functions and their identities.
- Example:
.
Applications in Engineering:
- Signal Processing:
- Trigonometric identities help analyze sound waves, electrical signals, and light waves by breaking them into components.
- Example: Fourier transforms use trigonometric identities to decompose complex waveforms.
- Structural Analysis:
- Engineering calculations involving loads, forces, and angles often use trigonometric identities for precision.
Related Topics
- The Fundamental Theorem of Arithmetic
- Mensuration
- Introduction To Circles
- Similarity of Triangles
- Probability
- Introduction To Trigonometry
- Some applications Of Trigonometry
- Introduction To Coordinate Geometry
- Trigonometric Ratios of Some Specific Angles
- Algebraic Methods of Solving a Pair of Linear Equations
- Introduction to Quadratic Equations
- Coordinate Geometry Distance Formula
- Pythagoras Theorem
- Sets
- Trigonometric Ratios



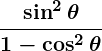
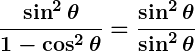 .
. .
.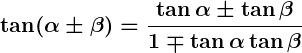






Get Social