What is Raoult’s Law?
Raoult’s Law, named after the French chemist François-Marie Raoult, is a fundamental principle of physical chemistry that describes the behavior of solutions. Established in 1887, it defines how the vapor pressure of the solvent is affected by the addition of a solute. Specifically, Raoult’s Law states that the partial vapor pressure of a solvent in a solution is directly proportional to the mole fraction of the solvent in the solution.
Mathematical Expression of Raoult’s Law
The law can be mathematically expressed as:
Where:
is the vapor pressure of the solution,
is the mole fraction of the solvent in the solution,
is the vapor pressure of the pure solvent.
This equation implies that the vapor pressure of a solution decreases as the amount of solute increases, assuming the solute is non-volatile.
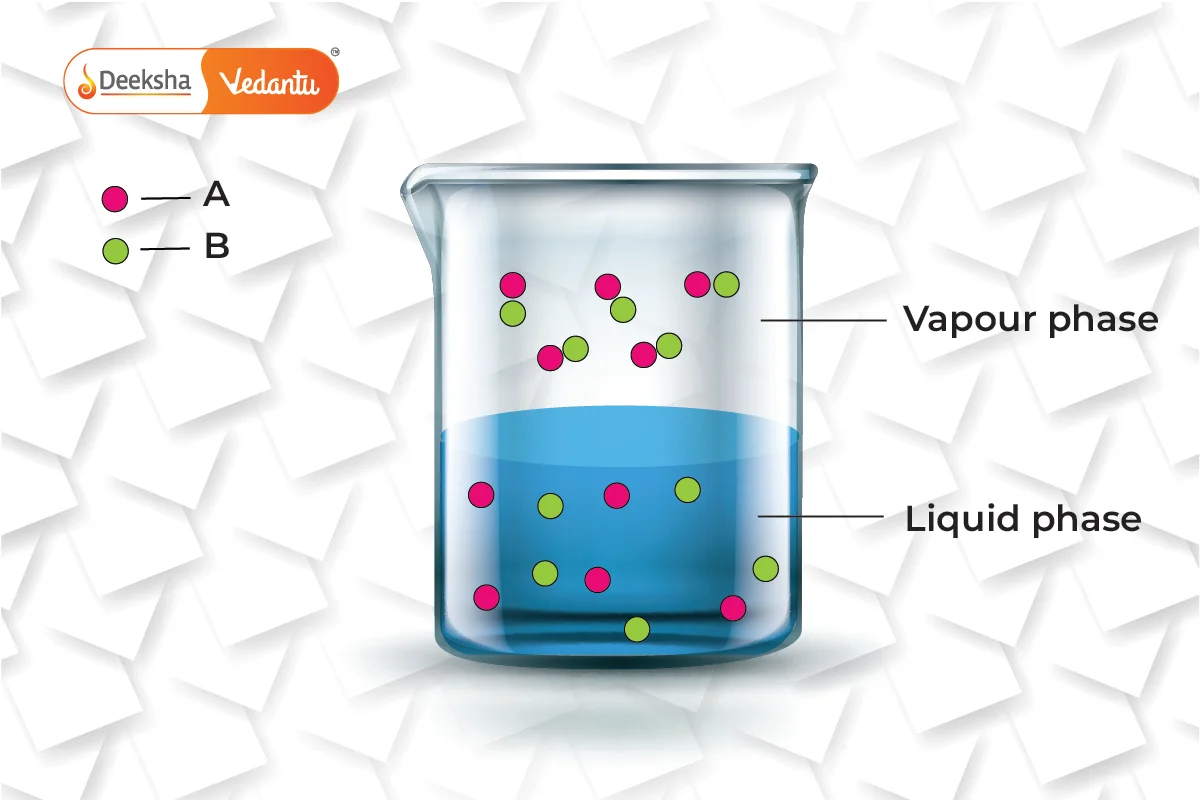
Practical Example to Illustrate Raoult’s Law
Consider a solution made from volatile liquids A and B. Both components contribute to the vapor pressure of the solution due to their volatility. According to Raoult’s law, the partial pressure exerted by each component is proportional to its mole fraction in the solution. Thus, the total pressure above the solution is the sum of the partial pressures of A and B.
Importance of Raoult’s Law
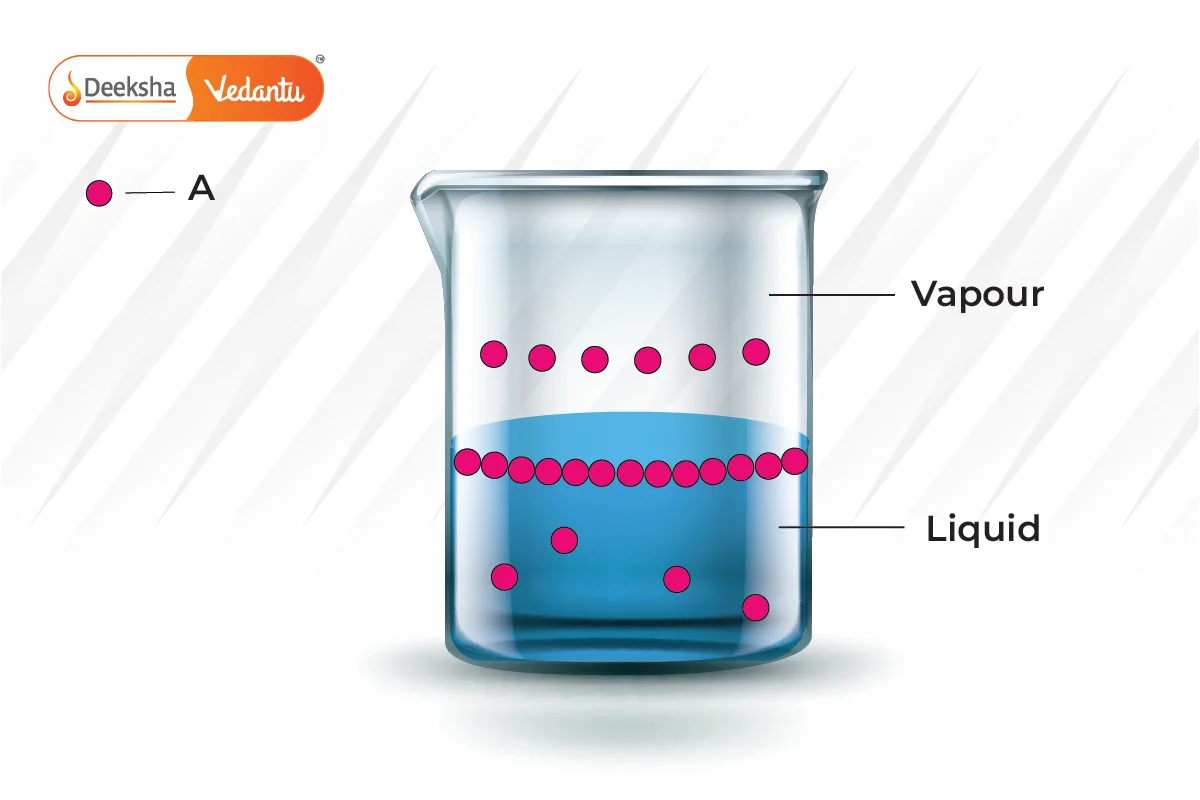
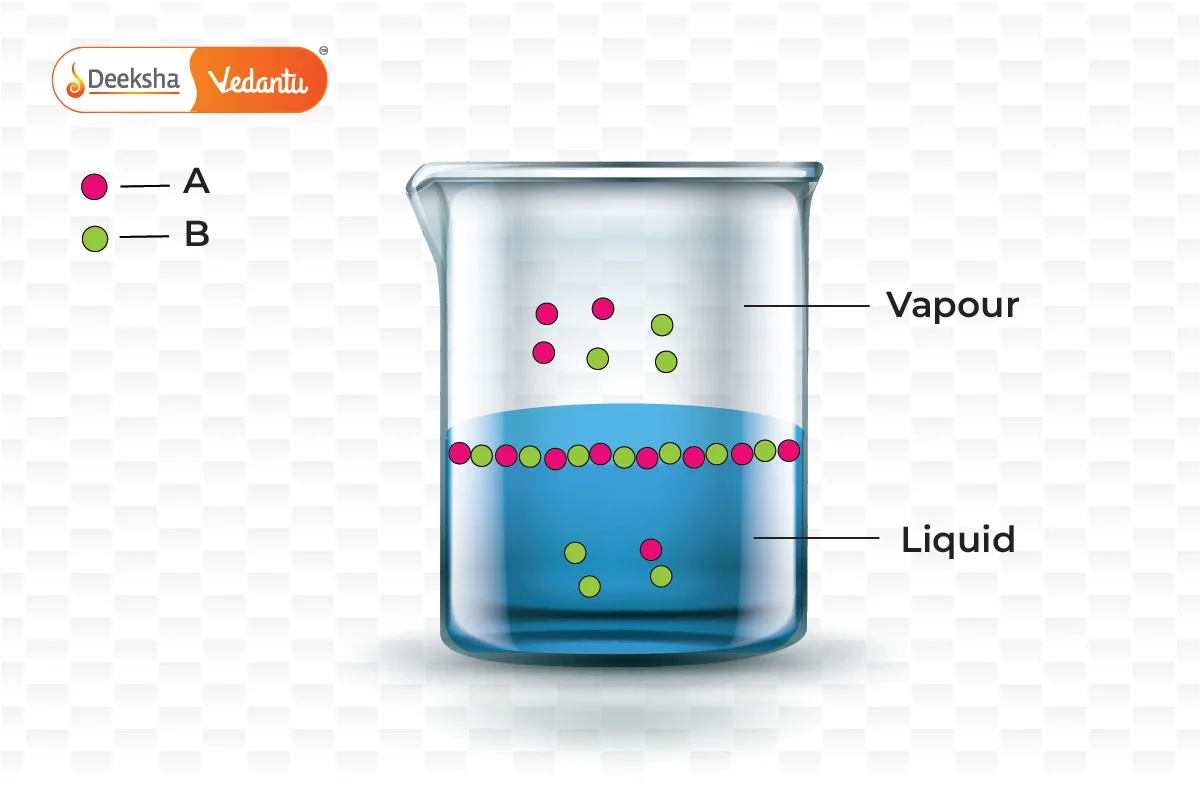
Raoult’s Law is crucial for understanding and predicting the boiling point elevation and freezing point depression in solutions. It helps chemists to:
- Determine the vapor pressure of solutions,
- Predict the behavior of solutions in distillation processes,
- Calculate the molecular masses of solutes based on changes in vapor pressure.
This new pressure (partial pressure) of each (A and B) is given by Raoult’s law and depends on the concentration of each component in the liquid phase.
From Raoult’s law, it is evident that as the mole fraction of a component reduces, its partial pressure also reduces in the vapour phase.
The graphs below show that pressure is the mole fraction for A and B.
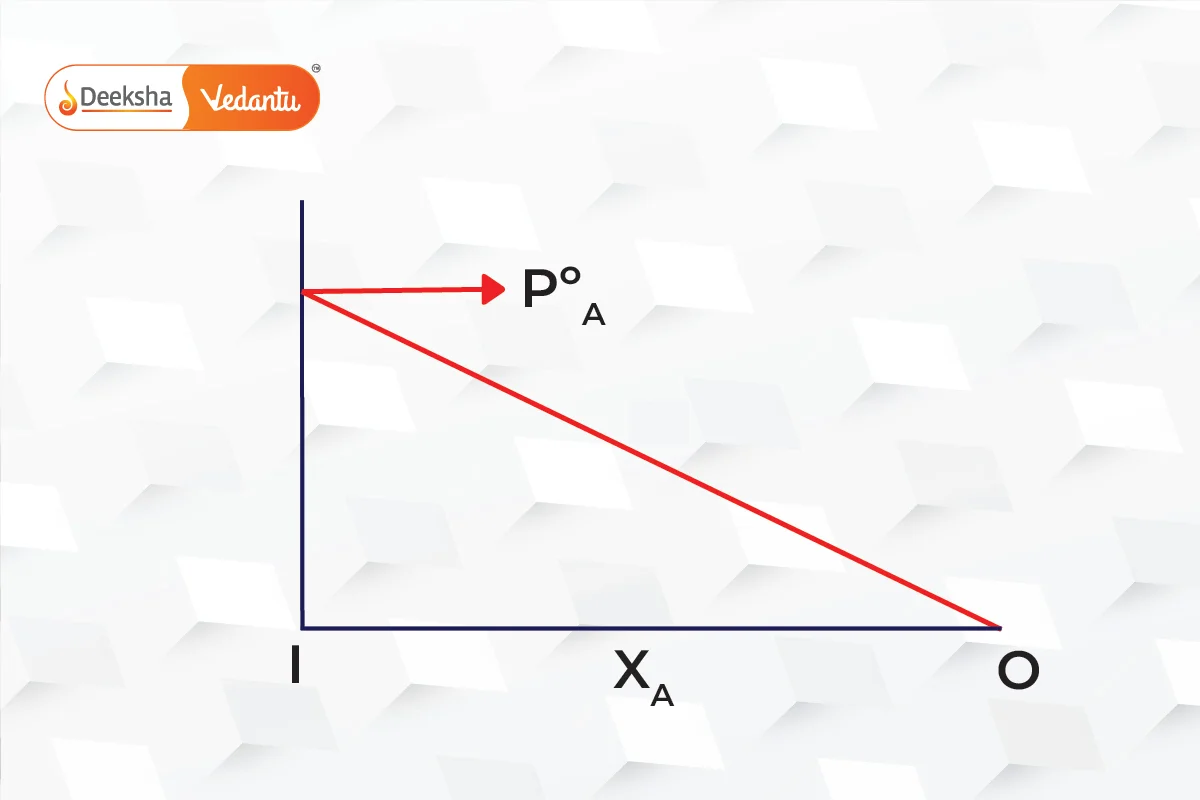

Combining both graphs,
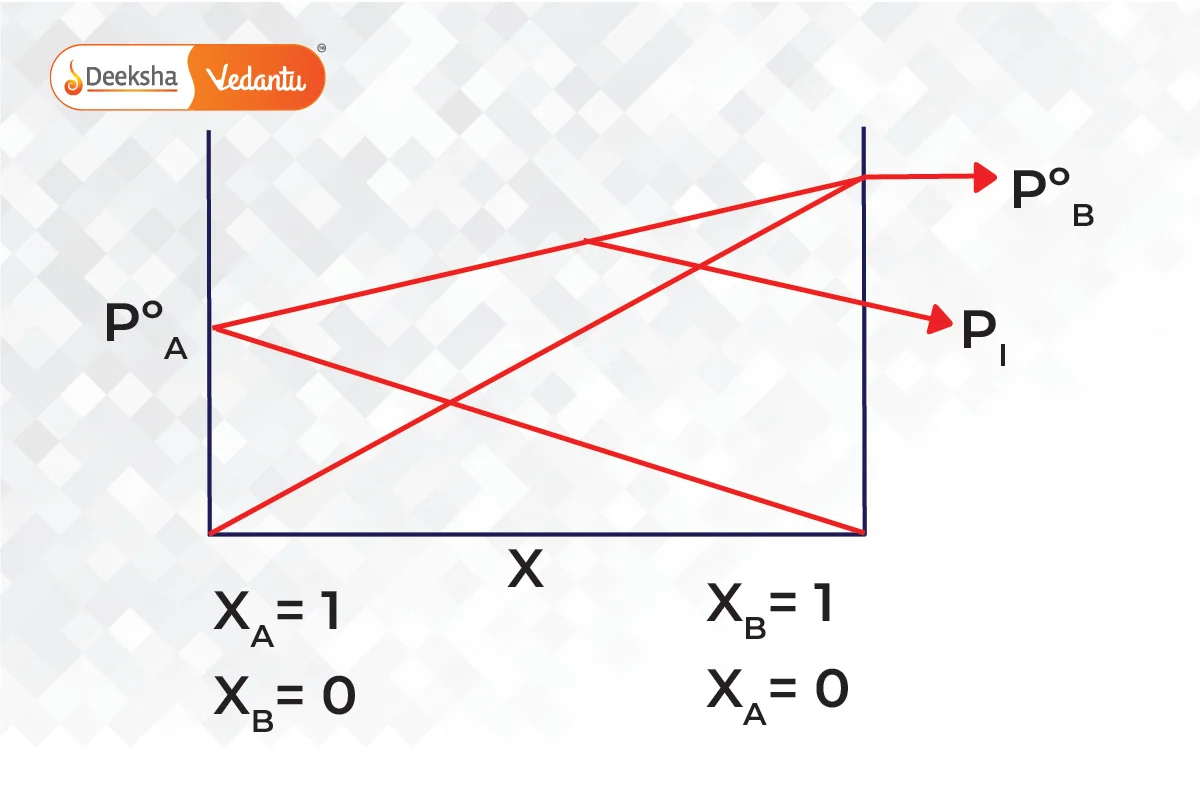
Raoult’s Law and Its Relationship with Other Laws
Raoult’s Law parallels the ideal gas law in that both predict the behavior of ideal mixtures. However, Raoult’s Law applies specifically to solutions where the solvent and solute interactions are similar to the solvent-solvent interactions. It also integrates well with Dalton’s Law of Partial Pressures in describing the total pressure of gaseous mixtures.
Here,
= mole fraction of component
in the solution,
= mole fraction in the gas phase.
Limitations of Raoult’s Law
While Raoult’s Law is widely applicable, it has limitations:
- It ideally applies to solutions where the interactions between different components are similar.
- Deviations occur in solutions where solute-solvent interactions are significantly different from solvent-solvent interactions. These deviations can be positive or negative, affecting the accuracy of predictions made using Raoult’s Law.
Applications of Raoult’s Law
Raoult’s Law is utilized in various chemical engineering and industrial processes:
- Designing distillation processes for separating mixtures,
- Manufacturing products with specific boiling or freezing characteristics,
- Analyzing the environmental impact of volatile organic compounds in the atmosphere.
FAQs
Temperature can affect the interactions between molecules in a solution, potentially leading to deviations from the predictions of Raoult’s Law.
While Raoult’s Law deals with the vapor pressure of the solvent in a solution, Henry’s Law focuses on the solubility of gases in liquids at constant temperature.
Yes, if the solute is non-volatile, Raoult’s Law can predict the decrease in vapor pressure due to the solute.
For non-ideal solutions, corrections are made using activity coefficients to account for deviations from ideal behavior.
Related Topics
- Coulomb’s Law
- Young’s Double Slit Experiment
- Atomic Structure
- JEE Main Syllabus 2025
- Rank of a Matrix and Some Special Matrices
- JEE Advanced Marks vs Ranks 2024
- Redox Reactions
- Heisenberg Uncertainty Principle
- JEE Main Marks vs Rank 2024
- Binomial Theorem
- Normality
- Simple Harmonic Motion (SHM)
- Semiconductors
- Transformer
- Electromagnetic Spectrum












Get Social