Introduction
In many electrical circuits, resistors are not used in isolation but are connected in various configurations to achieve desired current and voltage values. When resistors are connected in a circuit, they can be arranged in different combinations, namely series, parallel, or a combination of both. Understanding how to calculate the equivalent resistance of these arrangements is crucial for analyzing and designing electrical circuits.
In this section, we will discuss how to calculate the total or equivalent resistance for resistors connected in series and parallel, and understand how these combinations affect the flow of current in a circuit.
Resistors in Series
When resistors are connected in series, they are arranged end-to-end so that the same current flows through each resistor. The total or equivalent resistance of resistors in series is the sum of their individual resistances.

Formula for Resistors in Series:
The formula to calculate the equivalent resistance () for resistors connected in series is:
Where:
= Equivalent resistance of the resistors in series.
= Individual resistances of the resistors.
In this configuration:
- The same current flows through all the resistors.
- The total voltage across the series combination is the sum of the voltages across each resistor.
Example of Resistors in Series:
Suppose three resistors of values ,
,
are connected in series in a circuit. The equivalent resistance would be:
Thus, the total resistance of the circuit is . If a voltage of
is applied across the combination, the same current will flow through each resistor.
Characteristics of Series Combination:
- Current: The current through each resistor is the same, as there is only one path for the current to flow.
- Voltage: The voltage across each resistor is different and depends on the resistance value, but the total voltage is the sum of the individual voltage drops across each resistor.
Example:
If a current of 2 A flows through a series circuit with three resistors (), the voltage drop across each resistor can be calculated as:
- Voltage across
:
- Voltage across
:
- Voltage across
:
The total voltage across the combination is
Resistors in Parallel
When resistors are connected in parallel, they are connected across the same two points, providing multiple paths for the current to flow. The total or equivalent resistance of resistors in parallel is less than the resistance of the smallest individual resistor in the combination.
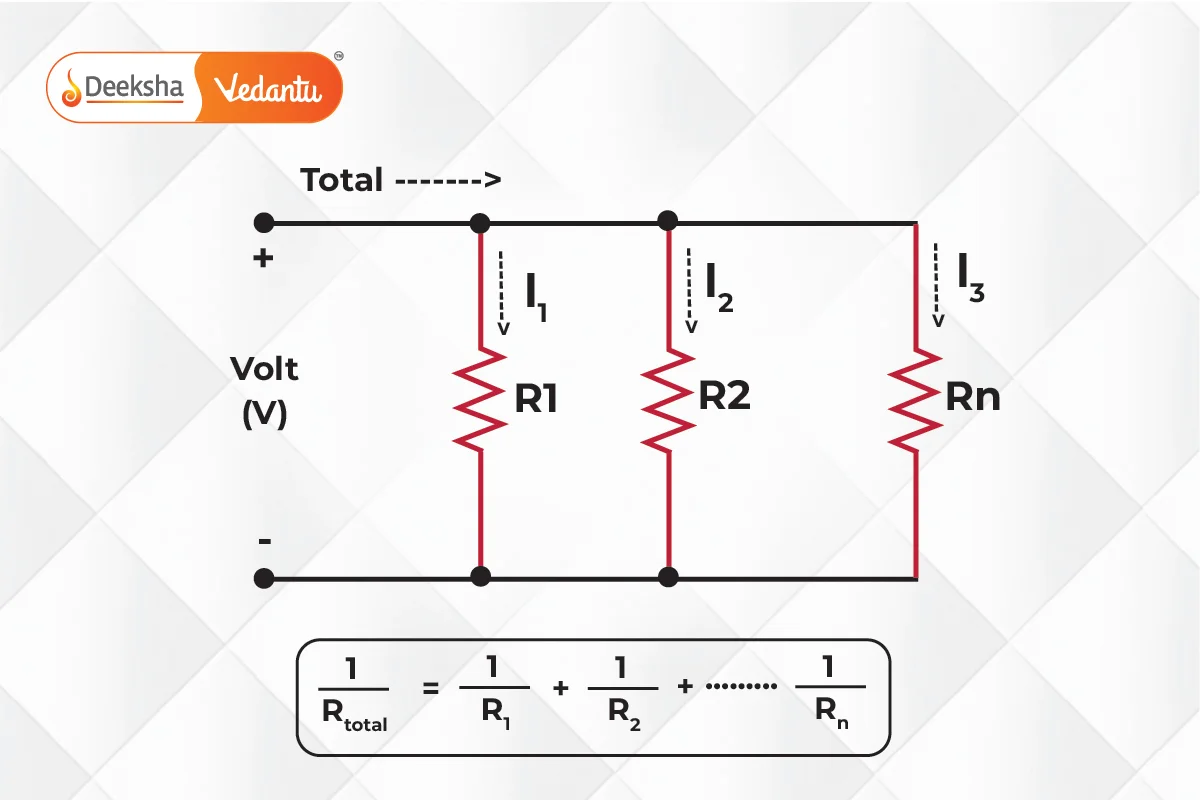
Formula for Resistors in Parallel:
The formula to calculate the equivalent resistance () for resistors connected in parallel is:
Where:
-
= Equivalent resistance of the resistors in parallel.
= Individual resistances of the resistors.
In this configuration:
- The voltage across each resistor is the same.
- The current through each resistor may differ depending on the resistance of each resistor.
Example of Resistors in Parallel:
Suppose two resistors of values and
are connected in parallel. The equivalent resistance would be calculated as:
Thus, the equivalent resistance is:
Characteristics of Parallel Combination:
- Voltage: The voltage across each resistor in parallel is the same as the voltage across the entire combination.
- Current: The current through each resistor is different and depends on the resistance of that resistor.
Example:
If a voltage of is applied across two parallel resistors (
and
):
- Current through the
resistor:
- Current through the
resistor:
Thus, the total current in the circuit is the sum of the individual currents:
Combination of Series and Parallel Resistors (Mixed Combination)
In many practical circuits, resistors are connected in both series and parallel combinations to achieve desired values of current and voltage. In such cases, the circuit is solved by simplifying the series and parallel parts step by step to find the total equivalent resistance.
Example of a Combination Circuit:
Suppose we have three resistors: two resistors of and
connected in series, and this combination is connected in parallel with another resistor of
.
Step 1: Calculate the equivalent resistance of the series combination:
Step 2: Calculate the equivalent resistance of the series combination in parallel with the 12 Ω resistor:
Thus, the equivalent resistance is:
Practical Applications of Series and Parallel Resistors
Household Wiring: In household electrical circuits, most appliances are connected in parallel so that each appliance receives the same voltage and can operate independently. If one appliance is switched off or malfunctions, the others continue to operate.
Electrical Devices: In electronic devices, resistors are used in both series and parallel combinations to achieve precise control of current and voltage. For example, in voltage dividers, resistors in series are used to reduce voltage to desired levels for specific components.
Voltage Regulation: Parallel resistors are often used in circuits where it is necessary to reduce the overall resistance to allow higher currents while maintaining the same voltage across each branch.
Key Practice Questions
Q1: Three resistors of ,
,
are connected in series. Calculate the total resistance.
- Answer:
Q2: Two resistors of and
are connected in parallel. Calculate the equivalent resistance.
- Answer:
Q3: A circuit consists of a 12 V battery connected in series with two resistors ( and
) and then in parallel with a third resistor (
). Calculate the equivalent resistance of the circuit.
- Answer:
FAQs
In a series circuit, the current remains the same throughout all resistors, but the voltage is divided among them. In a parallel circuit, the voltage is the same across all resistors, but the current is divided among the different branches.
In a parallel circuit, the current has multiple paths to travel through. Even if one of the resistors has a high resistance, the presence of other resistors provides additional paths for the current, reducing the total resistance.
When more resistors are added in parallel, the total resistance decreases because the current has more paths to flow through, reducing the overall opposition to current flow.
When more resistors are added in series, the total resistance increases because the current has to pass through each resistor, increasing the overall opposition to current flow.



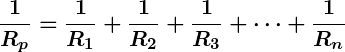
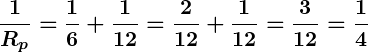
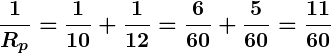
![Rendered by QuickLaTeX.com \[\displaystyle\boldsymbol{\frac{1}{R_p} = \frac{1}{5} + \frac{1}{10} = \frac{2}{10} + \frac{1}{10} = \frac{3}{10}}\]](https://deekshalearning.com/wp-content/ql-cache/quicklatex.com-4682777c6fb4cbf3adac4623269d32be_l3.png)
![Rendered by QuickLaTeX.com \[\displaystyle\boldsymbol{\frac{1}{R_p} = \frac{1}{9} + \frac{1}{4} = \frac{4}{36} + \frac{9}{36} = \frac{13}{36}}\]](https://deekshalearning.com/wp-content/ql-cache/quicklatex.com-07aa91d36910e7aaff4f98c8bba522ed_l3.png)






Get Social