Introduction
The zeroes of a polynomial and its coefficients have a specific relationship that helps in analyzing polynomial equations without explicitly solving them. This relationship is particularly useful for quadratic and cubic polynomials, where the sum and product of the zeroes can be directly connected to the coefficients of the polynomial. Here, we explore this relationship with examples for better understanding.
Zero of a Linear Polynomial
For a linear polynomial of the form , the zero is given by:
This simple formula connects the coefficient of (
) with the constant term (
).
Relationship for Quadratic Polynomials
For a quadratic polynomial , where
, let
and
be the zeroes. Then, the sum and product of the zeroes can be expressed in terms of the coefficients as follows:
- Sum of Zeroes:
Here,is the negative of the coefficient of
divided by the coefficient of
.
- Product of Zeroes:
This represents the constant term () divided by the coefficient of
.
Derivation of Sum and Product Formulas
In general, if and
are the zeroes of the quadratic polynomial
, where
, then
and
are factors of
. Thus, we can write:
where is a constant.
Expanding this, we get:
Comparing the coefficients of ,
, and the constant term on both sides, we obtain:
Since , dividing both equations by
gives:
Example for Quadratic Polynomials
Consider the polynomial .
- Factorizing: We split the middle term to get:
- Zeroes: The zeroes are
and
.
- Sum of Zeroes:
- Product of Zeroes:
This example confirms that the sum and product of the zeroes follow the derived relationships.
Further Examples for Quadratic Polynomials
- Example 2: Consider
.
- Zeroes: Solving, we find zeroes at
and
.
- Sum of Zeroes:
- Product of Zeroes:
- Zeroes: Solving, we find zeroes at
- Example 3: For the polynomial
, we find zeroes at
and
.
- Sum of Zeroes:
- Product of Zeroes:
- Sum of Zeroes:
Relationship for Cubic Polynomials
For a cubic polynomial , let
,
, and
be the zeroes. The relationships between the zeroes and coefficients are as follows:
- Sum of Zeroes:
- Sum of Product of Zeroes (taken two at a time):
- Product of Zeroes:
Example for Cubic Polynomial
Consider the polynomial .
- Given zeroes:
,
, and
.
- Verifying relationships:
- Sum of Zeroes:
- Sum of Product of Zeroes (two at a time):
- Product of Zeroes:
- Sum of Zeroes:
This confirms the relationships for cubic polynomials as well.
General Formulas
For a quadratic polynomial with zeroes
and
:
For a cubic polynomial with zeroes
,
, and
:
FAQs
This concept is widely used in algebra, calculus, and even fields like physics and engineering. For example, in circuit analysis, certain electrical parameters can be modeled using polynomial equations, and understanding the relationships between zeroes and coefficients can help solve complex problems efficiently.
For higher-degree polynomials (beyond cubic), similar relationships exist. The sum of zeroes, the sum of products of zeroes taken two at a time, and so on, can be related to the coefficients. However, the exact relationships depend on the polynomial’s degree and are more complex as the degree increases.
Yes, knowing the zeroes and their relationships with the coefficients allows us to construct polynomials. For example, if the zeroes of a quadratic polynomial are given as and
, we can write it as:
Expanding this will provide a polynomial with the desired zeroes.
This relationship allows us to determine properties of a polynomial without fully solving it. It is useful in factoring polynomials, solving equations, and understanding the behavior of polynomial functions in graphing and analysis.
For a linear polynomial , the zero is:
Yes, in a cubic polynomial , the sum of the products of zeroes taken two at a time is:
For a cubic polynomial , the product of the zeroes
,
, and
is given by:
For a cubic polynomial , if
,
, and
are the zeroes, then:
This is the sum of zeroes expressed in terms of the coefficients of and
.
For a quadratic polynomial , if
and
are the zeroes, then:
and
where represents the sum of zeroes, and
represents the product of zeroes.
Related Topics
- Algebraic Methods of Solving a Pair of Linear Equations
- Coordinate Geometry Section Formula
- Area of Triangle
- Criteria for Similarity of Triangles
- Sum of First n Terms of an AP
- Mensuration
- Differentiation Formulas
- Inches to Centimeters(cm) Converter
- Solution of a Quadratic Equation by Factorisation
- Trigonometric Identities
- Similarity of Triangles
- nth Term of an AP
- Trigonometry Formulas
- Maths FAQs
- Congruence of Triangles



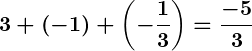
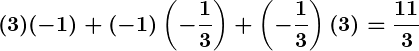



Get Social