In geometry, triangles are similar when they share the same shape, irrespective of their size. This happens when:
- Corresponding angles are equal.
- Corresponding sides are in the same ratio (proportion).
For example, if , then:
This concept is foundational in geometry and has practical applications in fields such as construction, navigation, and design.
Basic Proportionality Theorem (Thales’ Theorem)
Statement
If a line is drawn parallel to one side of a triangle, intersecting the other two sides, the line divides those sides in the same ratio.
In , if
, then:
Understanding Thales’ Theorem
Setup
- Draw any angle
and on one arm
, mark points
such that:
- Draw another arm
and mark a point
on it.
- From
, draw
.
Observations
Measure ,
,
, and
.
You will find:
This supports the Basic Proportionality Theorem.
Proof of Basic Proportionality Theorem
Given
In ,
intersects
and
at
and
.
To Prove
Construction
- Draw
and
.
Proof
- Area of
is proportional to its base
:
- Similarly, for
:
- Taking the ratio of areas:
Area of - Similarly, for
and
:
Area of - Thus,
.
Converse of Basic Proportionality Theorem
Statement
If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
Proof
- Suppose
.
- Assume
is not parallel to
.
- Draw
, and by the Basic Proportionality Theorem:
- But this contradicts
. Hence,
.
Examples Based on Theorems
Example 1: Prove
Solution:
From Thales' Theorem:
Adding 1 to both sides:
Thus:
Example 2: Prove in a trapezium.
Solution:
Join , intersecting
at
.
- Using Thales' Theorem in
:
- Similarly, in
:
Thus:
Example 3: Prove .
Solution:
, so by Thales' Theorem:
(corresponding angles).
Thus, .
Practice Problems
- In
, prove that
when
.
- Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
- In
,
. If
cm,
cm, and
cm, find
.
Related Topics
- Introduction to Arithmetic Progressions
- Differentiation Formulas
- Algebraic Methods of Solving a Pair of Linear Equations
- The Fundamental Theorem of Arithmetic
- Introduction to Triangles
- Trigonometry Formulas
- Sum of First n Terms of an AP
- Graphical Method of Solution of a Pair of Linear Equations
- nth Term of an AP
- Congruence of Triangles
- Maths FAQs
- Probability
- Pair of Linear Equations in Two Variables
- Roman Numerals
- Revisiting Irrational Numbers



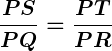








Get Social