What is Acceleration?
Acceleration is defined as the rate at which an object’s velocity changes over time. It is a vector quantity, meaning it has both magnitude and direction. Acceleration can occur due to changes in the speed of an object or due to changes in its direction of motion.
- Formula for Acceleration:
The basic formula for acceleration () is:
Where:is the acceleration,
is the change in velocity,
is the time taken for this change.
- The SI unit of acceleration is meters per second squared (
).
Types of Acceleration
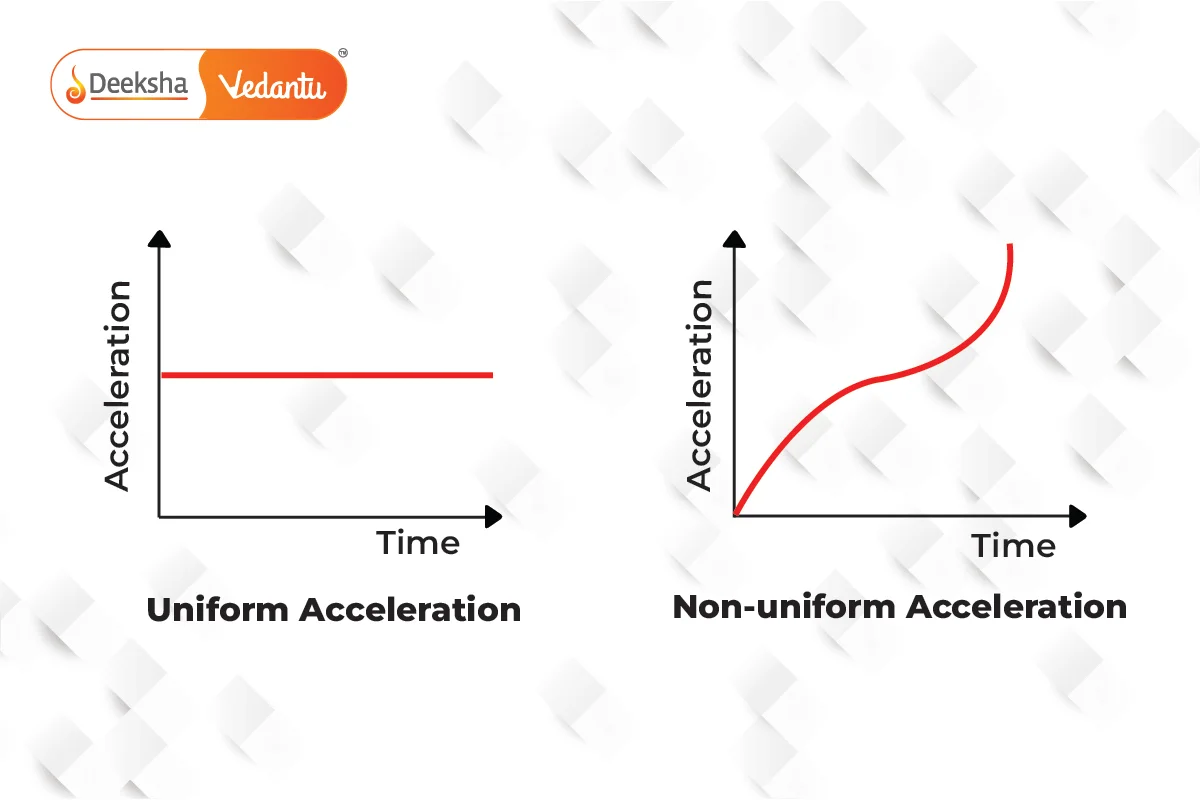
- Uniform Acceleration:
- In uniform acceleration, the rate of change of velocity remains constant over time. In other words, the object’s velocity changes by an equal amount in every equal interval of time.
- Example: A freely falling object under the influence of gravity is an example of uniform acceleration. The object’s velocity increases at a constant rate
on Earth).
- Non-Uniform (Variable) Acceleration:
- In non-uniform acceleration, the velocity of the object changes by varying amounts over equal time intervals. This means the rate of change of velocity is not constant.
- Example: A car that speeds up and slows down while driving experiences non-uniform acceleration.
- Centripetal Acceleration:
- Centripetal acceleration occurs when an object moves in a circular path at a constant speed, but its direction of motion is continuously changing. The object experiences acceleration directed toward the center of the circle.
- Example: A car turning around a curve experiences centripetal acceleration.
Relationship Between Acceleration and Velocity
- Positive Acceleration:
When an object speeds up, its acceleration is in the same direction as its velocity, and this is known as positive acceleration. - Negative Acceleration (Deceleration):
When an object slows down, its acceleration is opposite to the direction of its velocity, and this is known as negative acceleration or deceleration.

Equations of Motion Involving Acceleration
In Class 10 CBSE Physics, the equations of motion are used to solve problems involving uniform acceleration. These equations relate displacement, velocity, acceleration, and time.
- First Equation of Motion:
Where:is the final velocity,
is the initial velocity,
is the acceleration,
is the time taken.
- Second Equation of Motion:
Where:is the displacement,
is the initial velocity,
is the acceleration,
is the time taken.
- Third Equation of Motion:
Where:is the final velocity,
is the initial velocity,
is the acceleration,
is the displacement.
Applications of Acceleration
- Vehicles:
Acceleration plays a crucial role in how cars and other vehicles operate. When you press the accelerator pedal, you increase the vehicle’s speed, which is a change in velocity. Similarly, when brakes are applied, the vehicle undergoes deceleration. - Free Fall:
Objects falling freely under gravity experience constant acceleration. This phenomenon is observed in parachuting, where the person initially accelerates but eventually reaches terminal velocity due to air resistance. - Sports:
Acceleration is a key factor in various sports, such as running, cycling, and racing. Athletes train to increase their acceleration to improve their performance in races or matches. - Spacecraft Launches:
Spacecraft experience acceleration during launch, where engines provide the necessary force to overcome Earth’s gravitational pull and propel the spacecraft into space.
Numerical Example: Calculating Acceleration
Example 1: Calculating Acceleration from Change in Velocity
A car starts from rest and reaches a velocity of in
. What is the acceleration of the car?
Given:
- Initial velocity,
- Final velocity,
- Time taken,
Using the formula:
Thus, the acceleration of the car is .
Example 2: Finding Final Velocity Using Acceleration
A bus moving with an initial velocity of accelerates at a constant rate of
for
. Find the final velocity of the bus.
Given:
- Initial velocity,
- Acceleration,
- Time,
Using the first equation of motion:
Thus, the final velocity of the bus is .
Example 3: Finding Acceleration of a Free Falling Object
An object is dropped from a height, and it takes to hit the ground. Assuming the object is in free fall and the acceleration due to gravity is
, what is the velocity just before it hits the ground?
Given:
- Initial velocity,
(since the object starts from rest)
- Acceleration due to gravity,
- Time,
Using the equation:
Thus, the velocity just before hitting the ground is .
Example 4: Calculating Distance Covered Using Acceleration
A motorcycle starts from rest and accelerates at for
. Calculate the total distance covered by the motorcycle in this time.
Given:
- Initial velocity,
- Acceleration,
- Time,
Using the second equation of motion:
Since the initial velocity , the equation simplifies to:
Thus, the motorcycle covers a distance of in
.
Example 5: Finding Time to Stop Using Deceleration
A car traveling at applies brakes, causing a deceleration of
. How long will it take for the car to come to a stop?
Given:
- Initial velocity,
- Final velocity,
(since the car comes to a stop)
- Deceleration,
Using the first equation of motion:
Rearranging to solve for time ():
Thus, it will take the car to come to a stop.
FAQs
Yes, apparent weight can change when an object accelerates (e.g., feeling heavier or lighter in an elevator).
Acceleration can be measured using an accelerometer or by calculating the change in velocity over time using speed-measuring devices.
Gravity is a type of acceleration, specifically 9.8 m/s² downward near Earth’s surface, affecting all objects in free fall.
Uniform acceleration occurs when an object’s velocity changes by the same amount in equal intervals of time.
Negative acceleration (or deceleration) occurs when an object slows down, meaning its velocity decreases over time.
Yes, an object can have acceleration even if its speed is constant, as in the case of centripetal acceleration, where only the direction of velocity changes (e.g., circular motion).
Speed is the rate of change of distance, while acceleration is the rate of change of velocity.
The SI unit of acceleration is meters per second squared ().
Related Topics
- Refraction Of Light
- Zener Diode
- Reflection Of Light
- Magnetic Field And Field Lines
- Pressure
- Wheatstone Bridge
- Compound Microscope
- What is Hypothesis?
- P-N Junction
- Factors On Which The Resistance Of A Conductor Depends
- Kirchhoff’s Law
- Spherical Mirrors
- Circuit Diagram
- Protection Against Earthquake
- Fleming’s Left-Hand Rule and Right-Hand Rule












Get Social