Introduction
In Class 9, you learned about irrational numbers and some of their properties. You studied how rational and irrational numbers together make up the set of real numbers and learned how to locate irrationals on the number line. However, we didn't formally prove their irrationality. In this section, we will use proof by contradiction to establish that numbers like ,
, and
are irrational.
A number is considered irrational if it cannot be expressed in the form , where
and
are integers and
. Examples of irrational numbers include:
- Non-repeating, non-terminating decimals like
Theorem for Proving Irrationality
To prove that numbers like and
are irrational, we need an important theorem based on the Fundamental Theorem of Arithmetic.
Theorem 1: If is a prime number and
divides
, then
must also divide
, where
is a positive integer.
This theorem is crucial for proving the irrationality of certain square roots.
Proof of Theorem 1:
- Let the prime factorization of
be
, where
are prime factors (not necessarily distinct).
- Then,
.
- If
divides
, then by the Fundamental Theorem of Arithmetic,
must be one of the prime factors of
.
This theorem is essential in proving that numbers like are irrational by contradiction.
Proving that  is Irrational
is Irrational
To show that is irrational, we use proof by contradiction.
Proof:
- Assume, to the contrary, that
is rational.
- Then we can write
, where
and
are integers with no common factors other than 1 (i.e., they are coprime).
- Squaring both sides, we get
, which simplifies to
.
- Since
is divisible by 2,
must also be divisible by 2 (by Theorem 1). Let
for some integer
.
- Substituting
into
, we get
, which simplifies to
or
.
- This shows that
is divisible by 2, so
must also be divisible by 2.
Since both and
are divisible by 2, they have a common factor of 2, which contradicts our assumption that
and
are coprime.
Conclusion: This contradiction proves that is irrational.
Proving that  is Irrational
is Irrational
The proof for follows a similar pattern.
Proof:
- Assume, to the contrary, that
is rational, so
, where
and
are coprime integers.
- Squaring both sides, we get
, which implies
.
- Since
is divisible by 3,
must also be divisible by 3 (using Theorem 1). Let
for some integer
.
- Substituting
into
, we get
, which simplifies to
, or
.
- This shows that
is divisible by 3, so
must also be divisible by 3.
Since both and
are divisible by 3, they have a common factor of 3, which contradicts the assumption that
and
are coprime.
Conclusion: This contradiction proves that is irrational.
Properties of Irrational Numbers
- Sum or Difference of a Rational and Irrational Number:
The sum or difference of a rational and an irrational number is always irrational. For example,is irrational.
- Product and Quotient of a Non-Zero Rational and an Irrational Number:
The product and quotient of a non-zero rational number and an irrational number are always irrational. For instance,and
are irrational.
Example Problems
Example 1: Prove that is irrational.
Solution:
- Assume, to the contrary, that
is rational.
- Then we can write
, where
and
are integers and
.
- Rearranging, we get
.
- Since
and 5 are rational, their difference
would also be rational.
This contradicts the fact that is irrational. Thus,
is irrational.
Example 2: Prove that is irrational.
Solution:
- Assume, to the contrary, that
is rational.
- Then
, where
and
are coprime integers.
- Rearranging, we get
.
- Since
is rational, this implies that
is rational, contradicting its known irrationality.
Therefore, is irrational.
FAQs
Yes, if a number is a perfect square, its square root is rational (e.g., ).
The result is always irrational, as shown in examples like .
The square root of a prime number cannot be expressed as a fraction, so it’s irrational. We use proof by contradiction and Theorem 1 to prove this.



 , which simplifies to
, which simplifies to 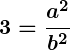 , which implies
, which implies 


Get Social