The mode of grouped data is a statistical measure that identifies the most frequently occurring value in a dataset. It is particularly significant in real-world scenarios as it helps highlight the most common outcomes or trends within a dataset, making it invaluable for market analysis, healthcare studies, and educational assessments. As a fundamental measure of central tendency, along with the mean and median, the mode plays an essential role in data analysis. In grouped data, the mode reveals the most common class interval, which helps in recognizing trends and patterns that are not immediately apparent from raw data alone. It is especially valuable when analyzing large data sets in fields such as economics, business, healthcare, and the social sciences.
Unlike in ungrouped data, where the mode can be directly observed, the mode of grouped data must be estimated through a specialized formula. This formula takes into account the class with the highest frequency—known as the modal class—as well as the frequencies of the surrounding classes. This approach allows for a more precise estimation of the mode and is widely applied in research, manufacturing quality control, and market surveys.
Key Concepts for Mode of Grouped Data
- Modal Class: The class interval with the highest frequency, representing the range in which the mode likely falls.
- Frequency (f): The number of observations recorded in each class interval. It reflects how many data points fall within that particular range.
- Class Mark (x): The midpoint of a class interval, calculated as the average of the upper and lower boundaries of the interval. Although not directly used in mode calculations, it is vital in other statistical measures.
- Class Width (h): The difference between the upper and lower boundaries of a class interval, helping standardize the size of each group for consistent analysis.
- Mode Formula for Grouped Data: This formula is particularly useful when analyzing large datasets where raw data is not readily available, and only grouped data is presented, such as in population surveys, economic reports, or academic performance studies.
- Where:
= lower boundary of the modal class
= frequency of the modal class
= frequency of the class preceding the modal class
= frequency of the class succeeding the modal class
= class width
- Importance of the Mode: In real-world applications, the mode helps reveal the most common characteristics in a dataset. It is particularly useful for categorical data, where numerical averages (mean) or midpoints (median) are less informative.
- Bimodal and Multimodal Distributions: Some datasets may have two or more classes with the same highest frequency, leading to bimodal or multimodal distributions. This often occurs in real-world scenarios, such as income distribution where two income brackets dominate, or in market research where consumer preferences are split between two popular products. These patterns indicate the presence of multiple trends within the data, providing valuable insights for targeted analysis. Some datasets may have two or more classes with the same highest frequency, leading to bimodal or multimodal distributions. This indicates the presence of multiple trends within the data.
Step-by-Step Example: Calculating the Mode of Grouped Data
Example: Calculate the mode of the following grouped dataset to identify the most common score range, which can be useful in contexts such as determining the most frequent test scores among a group of students:
Class Interval | Frequency (f) |
10-20 | 5 |
20-30 | 8 |
30-40 | 12 |
40-50 | 6 |
50-60 | 3 |
Solution:
- Identify the modal class: The class with the highest frequency is
, which has a frequency of
.
- Apply the mode formula:
(the lower boundary of the modal class)
(frequency of the modal class)
(frequency of the class preceding the modal class)
(frequency of the class succeeding the modal class)
(class width)
- Substitute values into the formula:
Answer: The mode of the grouped data is .
Applications of Mode of Grouped Data
- Business and Marketing: Analyzing consumer preferences and identifying the most frequently purchased products or services.
- Economics: Detecting common income ranges, expenditure patterns, or dominant economic trends within large-scale datasets.
- Healthcare and Medicine: Monitoring the most frequently occurring symptoms or diseases in a given population, which helps prioritize healthcare resources.
- Education: Analyzing academic performance by identifying the most frequently occurring scores across large groups of students.
- Social Sciences: Understanding public opinion through survey responses, helping researchers identify prevailing attitudes and trends.
- Manufacturing: Ensuring consistent product quality by tracking the most frequent defects during production, leading to improved quality control measures.
- Environmental Studies: Tracking the most common temperature ranges, rainfall intervals, or pollution levels to assess environmental changes over time.
- Sports Analytics: Identifying players' most frequent scores or match outcomes to assess consistency and performance trends.



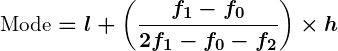
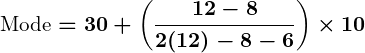
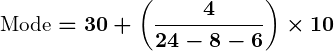




Get Social