Statistics is a vital branch of mathematics concerned with the collection, organization, analysis, interpretation, and presentation of data. It plays a crucial role in decision-making and prediction across various disciplines, including economics, biology, social sciences, engineering, business, and more. Through statistical methods, we can understand trends, analyze data patterns, make informed predictions, and solve real-world problems. In today’s data-driven world, statistical literacy is essential for making evidence-based decisions.
For Class 10 CBSE, statistics focuses primarily on understanding the measures of central tendency and graphical representation of data. This topic helps students develop analytical thinking by introducing key concepts like mean, median, and mode, which are used to summarize and interpret data effectively. Students will also learn how to visually represent data through graphs and charts such as histograms, frequency polygons, and ogives. Mastery of these concepts builds a strong foundation for future mathematical studies and applications in diverse fields.
Key Concepts in Statistics
- Data: A structured collection of facts, numbers, or observations gathered from experiments, surveys, or research. Data can be categorized into:
- Primary Data: Directly collected from original sources through surveys, experiments, or first-hand observations.
- Secondary Data: Derived from pre-existing sources, such as published reports, research papers, databases, or government records.
- Types of Data:
- Ungrouped Data: Unorganized raw data presented as it was collected.
- Grouped Data: Data arranged systematically into groups or classes, often presented in a frequency distribution table.
- Frequency Distribution Table: A table that organizes grouped data into intervals, showing how frequently each range of values occurs within the dataset.
- Cumulative Frequency: The running total of frequencies in a dataset that shows the cumulative number of observations up to a particular class interval.
- Class Interval: The range of data values grouped together into classes. Each interval represents a specific range of values within a dataset.
- Class Mark: The midpoint of a class interval used for further statistical calculations. It is calculated using:
- Range: The difference between the highest and lowest values in the dataset, providing a measure of data spread.
- Relative Frequency: The proportion of the total frequency represented by each class interval.
Measures of Central Tendency
The three most common measures of central tendency are:
- Mean (Average): Represents the arithmetic average of a dataset. It is the sum of all data values divided by the number of observations.
- For ungrouped data:
- For grouped data:
- For ungrouped data:
- Median: The middle value of an ordered dataset, dividing the data into two equal halves. For grouped data, the median is calculated using:
- Where:
= lower boundary of the median class
= total frequency
= cumulative frequency preceding the median class
= frequency of the median class
= class width
- Mode: The most frequently occurring value in the dataset. For grouped data:
- Where:
= lower boundary of the modal class
= frequency of the modal class
= frequency of the class preceding the modal class
= frequency of the class succeeding the modal class
= class width
Graphical Representation of Data
Visualizing data helps interpret large datasets and identify trends more easily. Common graphical methods include:
- Histogram: A bar graph used to represent grouped data. Class intervals are plotted on the x-axis, while frequencies are displayed on the y-axis.
- Frequency Polygon: A graph created by connecting the midpoints of histogram bars with straight lines. It visually represents the distribution of data.
- Ogive (Cumulative Frequency Curve): A curve that shows cumulative frequency distribution. It helps in estimating medians, quartiles, and percentiles.
- Pie Chart: A circular graph divided into sectors, where each sector represents a portion of the total dataset.
- Bar Graph: A visual tool that represents categorical data using rectangular bars proportional to the frequency of each category.
Examples with Step-by-Step Solutions
Example 1: Calculate the mean of the following data:
| Class Interval | Frequency |
| 10-20 | 5 |
| 20-30 | 8 |
| 30-40 | 10 |
| 40-50 | 7 |
| 50-60 | 5 |
Solution:
- Find the class marks:
- For 10-20:
, for 20-30:
, and so on.
- Multiply frequency by class mark:
| Class Interval | Frequency (f) | Class Mark (x) | |
| 10-20 | 5 | 15 | 75 |
| 20-30 | 8 | 25 | 200 |
| 30-40 | 10 | 35 | 350 |
| 40-50 | 7 | 45 | 315 |
| 50-60 | 5 | 55 | 275 |
- Calculate the mean:
Answer: The mean is approximately .
Example 2: Calculate the median of the following data:
| Class Interval | Frequency |
| 0-10 | 4 |
| 10-20 | 6 |
| 20-30 | 8 |
| 30-40 | 10 |
| 40-50 | 2 |
Solution:
- Calculate cumulative frequency:
| Class Interval | Frequency | Cumulative Frequency |
| 0-10 | 4 | 4 |
| 10-20 | 6 | 10 |
| 20-30 | 8 | 18 |
| 30-40 | 10 | 28 |
| 40-50 | 2 | 30 |
Find median class:, which lies in the
interval.
- Apply the formula:
Answer: The median is .
Applications of Statistics
Statistics plays a pivotal role in various domains, including:
- Economics: Analyzing market trends, inflation rates, GDP growth, and employment statistics.
- Healthcare: Studying patient recovery rates, drug effectiveness, and tracking disease outbreaks.
- Education: Evaluating academic performance, analyzing student attendance, and assessing teacher effectiveness.
- Social Sciences: Conducting surveys on social behavior, demographics, and public opinion polls.
- Sports: Analyzing player performance, predicting outcomes, and strategizing game plans based on past data.
- Business: Tracking sales, analyzing customer satisfaction, and optimizing marketing strategies based on data-driven insights.



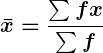
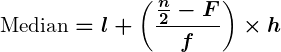
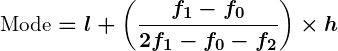
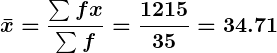
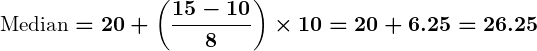







Get Social