What is Coordinate Geometry?
Coordinate Geometry, or analytic geometry, connects algebra and geometry by representing geometric shapes and problems using equations. Each point on a plane is represented by an ordered pair:
where:
is the horizontal distance (abscissa).
is the vertical distance (ordinate).
Why Learn the Section Formula?
The section formula helps locate a point that divides a line segment joining two points in a given ratio. It is widely applicable in:
- Engineering and Design: To proportionally divide structures or objects.
- Navigation and Mapping: Locating intermediate points between destinations.
- Graphics and Animation: Rendering positions in 2D models.
- Physics: Analyzing motion along a straight line.
Section Formula
The section formula provides the coordinates of a point dividing a line segment joining two points
and
in the ratio
:
Special Cases:
- Midpoint Formula:
When the dividing pointdivides the line segment into equal parts (
):
- Centroid of a Triangle:
The pointthat divides each median of a triangle into a ratio of
(vertex to midpoint):
- Distance Formula:
The distancebetween two points
and
is given by:
- External Division Formula:
When a pointdivides the line segment externally in the ratio
, the formula is:
- Slope of a Line:
The slopeof a line passing through two points
and
is:
Section Formula
Definition:
The section formula helps determine the coordinates of a point that divides a line segment joining two points
and
in a given ratio
. This formula is crucial for solving problems in geometry where proportional division of line segments is required.
Formula:
The coordinates of the point are given by:
Where:
: Represents the coordinates of the dividing point.
and
: Are the coordinates of the endpoints of the line segment.
: Denotes the ratio in which the point divides the line segment.
and
are positive constants.
Derivation of the Section Formula:
To derive the formula for the coordinates of a point that divides a line segment joining two points
and
in the ratio
.
Step-by-Step Derivation
- Consider a Line Segment:
- Let
and
be the endpoints of the line segment.
- Let
be the point dividing
in the ratio
.
- Let
- Proportionality:
- The division ratio implies:
- This means that the distance
is
parts, and
is
parts.
- The division ratio implies:
- Use of Coordinates:
- In coordinate geometry, the distances along the x-axis and y-axis are proportional to the division ratio.
- Let the x-coordinate of
be
, and the y-coordinate be
.
- Apply Proportionality Along the X-Axis:
- The position of
along the x-axis is determined by the weighted average of
and
:
- Cross-multiply to get: n
- Expand and rearrange:
- Solve for
:
- The position of
- Apply Proportionality Along the Y-Axis:
- Similarly, for the y-coordinate of
:
- Cross-multiply and solve as done for
:
- Solve for
:
- Similarly, for the y-coordinate of
- Combine Results:
- The coordinates of
are:
- The coordinates of
Applications of the Section Formula:
- Internal Division:
- When the point lies between the two endpoints of the line segment, the section formula is applied as:
- When the point lies between the two endpoints of the line segment, the section formula is applied as:
- External Division:
- When the point divides the line segment externally, the formula becomes:
Here,to ensure valid results.
- When the point divides the line segment externally, the formula becomes:
- Special Cases:
- Midpoint Formula:
If, the formula simplifies to:
- Centroid of a Triangle:
When dividing the medians of a triangle in the ratio:
- Midpoint Formula:
- Distance Formula (for verifying calculations):
The distance between two pointsand
is:
- Slope of a Line:
The slope of a line passing through two pointsand
is:
Types of Division
Internal Division
Internal division occurs when the point lies between the two endpoints of a line segment
and
. This means that the point divides the line segment internally in a specified ratio
.
- Formula for Internal Division:
- Explanation:
and
represent the weights of division, such that:
- The formula calculates the weighted average of the coordinates of
and
.
- Example: Find the coordinates of a point dividing the line segment joining
and
in the ratio
.
- Using the internal division formula:
.
- Using the internal division formula:
External Division
External division occurs when the point lies outside the line segment, such that it divides the line segment
and
externally in a specified ratio
. This type of division happens when the line segment is extended beyond one of the endpoints.
- Formula for External Division:
- Explanation:
and
still represent the weights of division, but the subtraction in the formula reflects the external division.
- For valid results,
to ensure
.
- Example: Find the coordinates of a point dividing the line segment joining
and
externally in the ratio
.
- Using the external division formula:
.
- Using the external division formula:
Comparison of Internal and External Division
| Aspect | Internal Division | External Division |
| Position of Point | Lies between the endpoints of the line segment. | Lies outside the endpoints, beyond the line segment. |
| Formula | 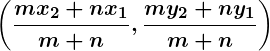 | 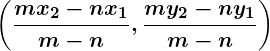 |
| Ratio Condition |
Solved Examples
Example 1: Internal Division
Problem:
Find the point dividing a line segment joining and
in the ratio
.
Solution: Using the section formula for internal division:
Substitute:
,
Simplify:
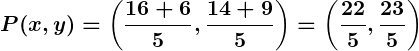
Example 2: External Division
Problem:
Determine the coordinates of a point dividing a line segment joining and
externally in the ratio
.
Solution: Using the section formula for external division:
Substitute:
,
Simplify:
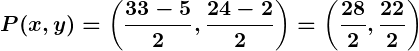

\boldsymbol{B(4, 5)}
\boldsymbol{C(7, 8)}
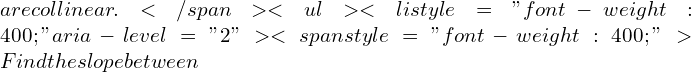
\boldsymbol{B}
\displaystyle\boldsymbol{m_1 = \frac{y_2 – y_1}{x_2 – x_1} = \frac{5 – 2}{4 – 1} = \frac{3}{3} = 1}
\boldsymbol{B}
\boldsymbol{C}
\displaystyle\boldsymbol{m_2 = \frac{y_2 – y_1}{x_2 – x_1} = \frac{8 – 5}{7 – 4} = \frac{3}{3} = 1}
\boldsymbol{m_1 = m_2}
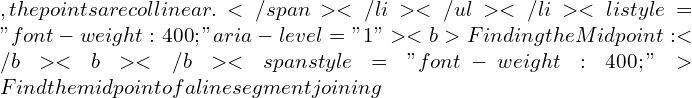
\boldsymbol{(6, -8)}
\displaystyle\boldsymbol{M(x, y) = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)}
\displaystyle\boldsymbol{M(x, y) = \left(\frac{-2 + 6}{2}, \frac{4 – 8}{2}\right) = \left(\frac{4}{2}, \frac{-4}{2}\right) = \left(2, -2\right)}$



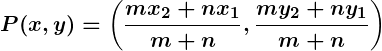


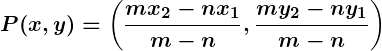
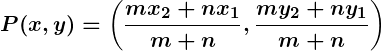
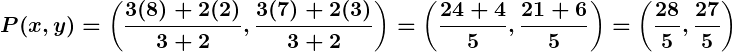
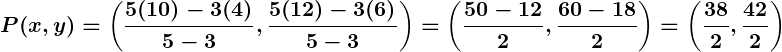
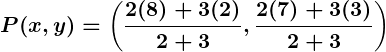
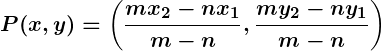
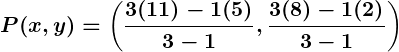








Get Social