Introduction to Trigonometry
Definition
Trigonometry is a branch of mathematics that studies the relationships between the angles and sides of triangles, particularly right-angled triangles. The word "trigonometry" comes from the Greek words "trigonon" (triangle) and "metron" (measure), meaning "measurement of triangles."
- Key Concept:
Trigonometry focuses on understanding how angles and their corresponding ratios (such as sine, cosine, and tangent) describe geometric properties and relationships. - Significance in Mathematics:
Trigonometry is fundamental in solving problems involving triangles and periodic phenomena. It extends beyond pure mathematics to practical applications in science, engineering, and technology.
Historical Background
- Origins:
Trigonometry has its roots in ancient civilizations such as Babylon and Egypt, where it was used for astronomy and building structures like pyramids. - Development:
- The Greeks, particularly Hipparchus (known as the "Father of Trigonometry"), formalized trigonometric concepts.
- Indian mathematicians like Aryabhata and Brahmagupta contributed significantly to the development of sine and cosine functions.
- Arabic scholars preserved and expanded on Greek and Indian trigonometry, introducing terms like "sine" and "tangent."
- During the European Renaissance, mathematicians like Johannes Kepler and Leonhard Euler advanced trigonometry for use in physics and astronomy.
Applications of Trigonometry
- Geometry:
- Solving for unknown sides or angles in triangles.
- Analyzing shapes like circles, polygons, and ellipses.
- Physics:
- Describing wave motion and oscillations.
- Calculating forces, velocities, and displacements in mechanics.
- Engineering:
- Designing and analyzing structures such as bridges and buildings.
- Creating accurate blueprints and CAD (computer-aided design) models.
- Astronomy:
- Measuring distances between celestial bodies.
- Calculating the orbits of planets and satellites.
- Navigation:
- Determining positions and plotting courses using triangulation.
- Calculating angles of elevation or depression for surveying.
Real-Life Examples
- Measuring Heights of Buildings or Trees:
Using the angle of elevation and a known distance, trigonometry helps calculate the height of tall objects. - Surveying and Mapping:
Trigonometry is used to determine distances and angles between land features. - Flight and Maritime Navigation:
Pilots and sailors use trigonometry to calculate direction and distance. - Wave Analysis:
Trigonometric functions model sound waves, light waves, and alternating current in electrical engineering.
Trigonometric Ratios
Definition
Trigonometric ratios are mathematical relationships between the lengths of the sides of a right triangle. These ratios are defined relative to one of the acute angles, , in the triangle. Trigonometric ratios form the foundation of trigonometry and are crucial for solving problems involving triangles, angles, and distances.
The Six Trigonometric Ratios
In a right triangle, let:
- The angle be
.
- The sides be labeled as:
- Opposite Side: The side opposite to the angle
.
- Adjacent Side: The side next to the angle
(excluding the hypotenuse).
- Hypotenuse: The longest side of the triangle, opposite the right angle.
- Opposite Side: The side opposite to the angle
The six trigonometric ratios are defined as follows:
- Sine (
):
- Cosine (
):
- Tangent (
):
- Cosecant (
):
- Secant (
):
- Cotangent (
):
Right Triangle Reference
To clearly understand the trigonometric ratios, consider a right triangle :
is the right angle.
.
The sides are labeled as:
- Opposite Side:
(opposite to
).
- Adjacent Side:
(next to
, excluding the hypotenuse).
- Hypotenuse:
(longest side, opposite the right angle).
Key Observations
- Trigonometric ratios depend on the angle
and not on the size of the triangle.
- The reciprocal relationships between the ratios are:
Trigonometric Ratios of Standard Angles
Angles
The standard angles in trigonometry are:
,
,
,
, and
.
These angles are frequently used in trigonometric calculations and have specific trigonometric ratio values.
Table of Ratios
The values of the six trigonometric ratios for the standard angles are:
Memorization Tips
- For
and
:
- Values of
follow the sequence:
- Values of
are the reverse of
:
- Values of
- For
:
. Memorizing
and
makes calculating
easier.
- Reciprocal Ratios:
,
,
.
- Mnemonic Device:
- For
:
"Some People Have Curious Senses" ().
- For
:
"Cats Sleep Perfectly Halved Opposite" ().
- For
Trigonometric Identities
Definition
Trigonometric identities are mathematical equations that are universally true for all values of , where the expressions involved are defined. These identities establish relationships between trigonometric functions and are fundamental tools for simplifying expressions and solving equations in trigonometry.
Key Identities
- Pythagorean Identities: These are derived from the Pythagorean theorem applied to a right triangle:
Applications of Trigonometric Identities
- Simplifying Trigonometric Expressions:
- Example: Simplify
.
Using the identity, the simplified expression is
.
- Example: Simplify
- Solving Trigonometric Equations:
- Example: Solve
.
Using the identity, substitute and solve for
.
- Example: Solve
- Verifying Identities:
- Example: Prove
.
Using, the left-hand side simplifies to
.
- Example: Prove
- Applications in Geometry and Physics:
- Simplify wave equations, analyze circular motion, and solve problems in mechanics and optics.
Tips for Using Identities
- Memorize the key identities as they form the foundation for most trigonometric problems.
- Practice rewriting expressions in terms of
and
to simplify.
- Use the identities to convert between functions like
,
,
, and
.
Applications of Trigonometry
1. Height and Distance Problems
Trigonometry is extensively used to solve problems involving heights and distances. The primary trigonometric ratios ,
, and
are used to calculate the height of an object or the distance between two points.
Key Concepts:
- Angle of Elevation:
The angle between the horizontal line and the line of sight when looking upward at an object.- Example: Measuring the height of a tower using
.
- Example: Measuring the height of a tower using
- Angle of Depression:
The angle between the horizontal line and the line of sight when looking downward at an object.- Example: Calculating the distance of a ship from a lighthouse using
.
- Example: Calculating the distance of a ship from a lighthouse using
Example: Calculating Height
- A person standing 50 meters away from the base of a tower observes the top of the tower at an angle of elevation of
. Find the height of the tower.
- Using
:
.
2. Real-Life Applications
Trigonometry is a critical tool in various real-world scenarios. Here are some of the key applications:
Construction and Architecture:
- Structural Design:
Engineers use trigonometry to calculate slopes, angles, and heights in designing buildings, bridges, and roofs. - Blueprint Measurements:
Trigonometric functions help ensure accurate dimensions in construction plans.
Navigation:
- Positioning and Triangulation:
Pilots and sailors use trigonometric principles to determine their location and plot courses.- Example: Calculating the distance of a ship from the shore by measuring the angle of elevation to a known height, such as a lighthouse.
Astronomy:
- Measuring Distances:
Astronomers use trigonometric parallax to measure the distance to stars and other celestial bodies. - Tracking Orbits:
Trigonometry helps analyze the motion of planets, moons, and satellites.
Physics:
- Wave Motion:
Trigonometric functions model oscillatory motion, such as sound waves, light waves, and alternating current. - Projectile Motion:
Trigonometry is used to analyze angles and distances in the trajectory of projectiles.
Example: Calculating Angle of Depression
- A drone is flying at a height of 100 meters and observes a car on the ground at an angle of depression of
. Find the horizontal distance between the drone and the car.
- Using
:
.




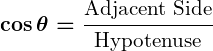


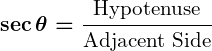


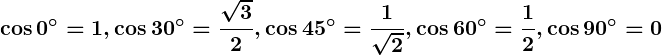
 ).
).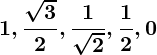 ).
). .
. .
.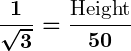
 .
.


Get Social