Trigonometric Functions – Class 11 Unit 3 Master Guide

Why This Unit Matters for JEE, NEET, KCET & COMEDK

Marks Weightage in Competitive Exams

JEE Main & Advanced: 2–3 questions (~8–12 marks)
NEET (Physics section): 1–2 questions indirectly (~4–8 marks)
KCET/COMEDK: 2–3 questions (~6 marks)

Understanding this unit improves performance not only in direct mathematics problems but also in physics applications across all these exams.

Trigonometry is one of the most foundational units in Class 11 Mathematics and acts as a bridge between algebra, geometry, and calculus. Its significance extends well beyond the classroom and finds immense applications in various branches of science and engineering.

In competitive exams like JEE, NEET, KCET, and COMEDK, Trigonometric Functions are not isolated; they are intricately linked with other mathematical domains – vectors, calculus, coordinate geometry, and even physics. These functions are essential for resolving vector components, working with oscillations, analyzing waveforms, and understanding circular and rotational motion.

In JEE (Main + Advanced), questions from this unit appear both directly and as part of more complex multi-concept problems. The unit carries a weightage of approximately 8–12%. In NEET, trigonometric understanding helps decode physics questions, particularly those in wave motion, optics, and kinematics. For KCET and COMEDK, formula-based and identity-driven problems are frequently tested with moderate complexity.

Mastery of trigonometric functions enhances:

Problem-solving speed and accuracy in time-bound exams
Algebraic manipulation and equation solving under calculus and vector topics
Understanding of periodic and oscillatory phenomena in both mathematics and physics
Strategic reasoning in graphical and transformation-based questions

Breakdown of Chapters in Unit 3: Trigonometric Functions

3.1 Introduction

This section traces the historical development of trigonometry, from its geometric beginnings to its transformation into a robust system of functions. Initially used for calculating angles and distances in triangles, trigonometry has now evolved into a study of periodic functions. Students learn how trigonometric ratios like sine, cosine, and tangent transition into real-valued functions with defined domains and ranges. These functions are extensively used to model periodic physical phenomena like sound waves, alternating currents, pendulum motion, and circular motion.

The introduction helps students visualize trigonometry not just as a formula-centric topic, but as a powerful analytical tool.

JEE/NEET Insight: Grasping this evolution allows students to appreciate the functional behavior of trigonometric identities and integrate them seamlessly into calculus and physics.

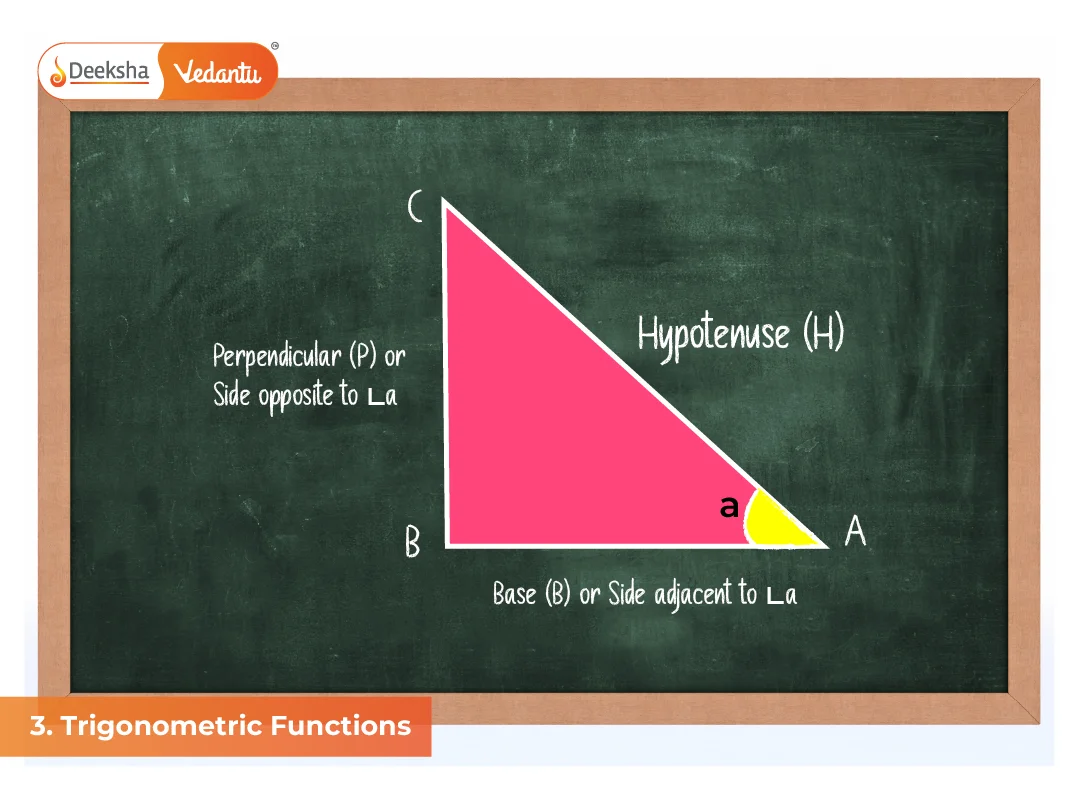
3.2 Angles

This chapter focuses on the measurement and classification of angles. Students explore the three primary angle measures – degrees, radians, and revolutions – and how to convert between them. The concept of direction, sign (positive or negative angles), and types (acute, obtuse, complementary, supplementary) are also introduced. Practical implications such as arc length and area of a sector are derived using radian measure.

Key concepts include:

Degree measure, radian measure, and revolution
Interconversion: 180° = π radians
Circular direction system for positive/negative angles
Length of arc (s = rθ) and area of sector (A = ½ r²θ)

Exam Relevance:

JEE/KCET/COMEDK: Expect questions on unit conversions and application-based problems involving arc length or area of a sector.
NEET Physics: Radial systems and angular displacement are key concepts in chapters like rotational motion and SHM.

3.3 Trigonometric Functions

This is the crux of Unit 3. Students generalize the idea of trigonometric ratios using the unit circle, allowing the domain to extend from acute angles to any real number. The quadrant system is introduced to determine the sign of trigonometric functions based on angle placement. Graphical understanding – plotting sine, cosine, and tangent – is emphasized to visualize periodicity and symmetry.

Topics covered:

Unit circle approach to define sin, cos, tan for all real angles
Quadrant-wise sign conventions (ASTC rule)
Graphs of sine, cosine, and tangent functions
Periodicity, amplitude, phase shift, domain and range, and symmetry

Competitive Edge:

JEE Advanced: Conceptual and graph-based problems are popular, testing students on transformations, composite functions, and domain analysis.
KCET/COMEDK: Direct substitution, identity application, and graphical inferences are common.
NEET Physics: Problems involving projection motion and wave analysis often require use of sin/cos graphs and values at standard angles.

3.4 Trigonometric Functions of Sum and Difference of Two Angles

In this critical section, students are introduced to compound angle identities, essential for simplifying complex expressions and solving trigonometric equations efficiently. These include:

sin(A ± B) = sinAcosB ± cosAsinB
cos(A ± B) = cosAcosB ∓ sinAsinB
tan(A ± B) = (tanA ± tanB) / (1 ∓ tanA·tanB)

Mastery of these identities aids in:

Reducing multi-angle expressions
Solving trigonometric equations
Proving identities and converting between forms

For example, evaluating values like sin(75°) or proving expressions like cos(45° + 30°) become easier using these formulas. Applications extend into simplifying physics derivations and algebraic transformations.

Also includes:

Problem-solving using compound angles
Application in proving trigonometric identities
Introduction to multiple and sub-multiple angle formulas (leading to further study in Class 12)

JEE Main/Advanced: Expect multi-step simplification problems and MCQs using these identities.
KCET/COMEDK: Frequent appearance in 1-mark and assertion-reason questions.
NEET: Though used indirectly, understanding these formulas helps in solving vector and motion-based physics problems.

Conclusion

Unit 3 of Class 11 NCERT Mathematics – Trigonometric Functions – is far more than just a syllabus requirement. It lays the groundwork for success in higher-level mathematics, physics, and engineering disciplines. With its wide applicability in real-world modeling, analytical reasoning, and scientific computation, this unit prepares students to handle competitive exam questions with speed and precision.

Whether you’re preparing for JEE, NEET, KCET, or COMEDK, mastering Unit 3 enables you to tackle advanced problems confidently and lays the conceptual foundation for Class 12 topics such as calculus, differential equations, and vector algebra.

Stay tuned as we dive into individual chapter explanations with solved examples, formula cheat-sheets, visual aids, MCQs, and strategic revision material curated for excellence in competitive exams.