10.6 Hyperbola – Class 11 Mathematics

Introduction

The hyperbola is the last and most intriguing conic section. It is obtained when a plane cuts both nappes of a double-napped right circular cone at an angle to the axis such that the plane is not parallel to the generating line. Unlike the ellipse, which is a closed curve, the hyperbola is an open curve consisting of two symmetrical branches extending to infinity.

Analytically, a hyperbola is defined as the locus of a point in a plane such that the absolute difference of its distances from two fixed points (foci) is constant.

Hyperbolas play a crucial role in physics (radio waves, optics), astronomy (orbits of comets), and engineering (navigation systems). For JEE, KCET, and COMEDK, hyperbola questions usually test equations, tangents, normals, asymptotes, and eccentricity-based properties.

Standard Definition

A hyperbola is the locus of a point P(x, y) such that:

|PF₁ – PF₂| = 2a (constant)

Where,

• F₁ and F₂ are two fixed points called foci.
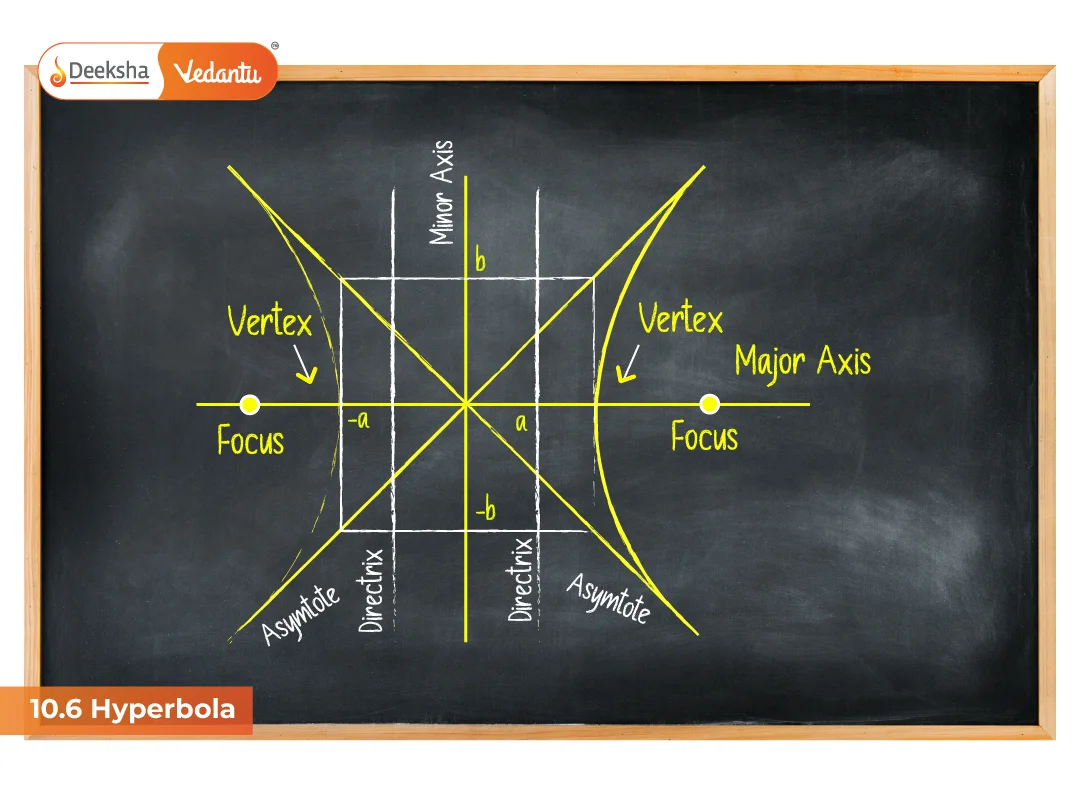
• The line through foci is called the transverse axis.
• The midpoint of the foci is the centre.
• The line perpendicular to the transverse axis through the centre is the conjugate axis.
• The distance a is the semi-transverse axis.

Derivation of Standard Equation

Let the centre be at origin (0, 0) and transverse axis along x-axis.
Foci: (–c, 0) and (c, 0)

For any point P(x, y):
|PF₁ – PF₂| = 2a

Squaring and simplifying yields:

x²/a² – y²/b² = 1

where c² = a² + b².

This is the standard equation of hyperbola with transverse axis along x-axis.

Standard Forms of Hyperbola

1. Transverse axis along x-axis:
   x²/a² – y²/b² = 1
   • Vertices: (±a, 0)
   • Foci: (±c, 0)
   • Asymptotes: y = ±(b/a)x
2. Transverse axis along y-axis:
   y²/a² – x²/b² = 1
   • Vertices: (0, ±a)
   • Foci: (0, ±c)
   • Asymptotes: x = ±(a/b)y

Key Elements

• Centre: (0, 0) in standard form.
• Vertices: Endpoints of transverse axis.
• Foci: (±c, 0) or (0, ±c) depending on orientation.
• Asymptotes: Straight lines that branches of hyperbola approach at infinity.
• Eccentricity (e): e = c/a > 1 for hyperbola.
• Latus rectum: Line through focus perpendicular to transverse axis, length = 2b²/a.

General Equation of Hyperbola

If centre is (h, k):

(x – h)²/a² – (y – k)²/b² = 1 (transverse axis horizontal)
(y – k)²/a² – (x – h)²/b² = 1 (transverse axis vertical)

Properties of Hyperbola

1. Symmetry: Symmetric about both axes and the centre.
2. Focal property: Difference of focal distances = 2a.
3. Asymptotes: Lines approached by hyperbola at infinity.
4. Reflective property: Ray from one focus reflects to the other.
5. Equation of transverse & conjugate axes: x-axis and y-axis respectively.

Equation of Tangent

1. At point (x₁, y₁) on hyperbola x²/a² – y²/b² = 1:

(xx₁)/a² – (yy₁)/b² = 1

1. Parametric form: For P(a secθ, b tanθ):

(x secθ)/a – (y tanθ)/b = 1

Equation of Normal

At P(a secθ, b tanθ):

(ax secθ)/a – (by tanθ)/b = a² + b²

(Simplified form used in exams)

Parametric Form

For x²/a² – y²/b² = 1, parametric representation is:
(x, y) = (a secθ, b tanθ)

Conjugate Hyperbola

If x²/a² – y²/b² = 1 is a hyperbola, then:

y²/b² – x²/a² = 1

is its conjugate hyperbola.

Asymptotes

For x²/a² – y²/b² = 1, asymptotes are:

y = ±(b/a)x

These help sketching hyperbolas and solving exam problems quickly.

Latus Rectum

Equation: x = c (or x = –c)
Length = 2b²/a

Solved Examples

Example 1: Equation of Hyperbola

Find the equation of hyperbola with vertices (±5, 0) and foci (±13, 0).

Solution:
a = 5, c = 13 → b² = c² – a² = 169 – 25 = 144 → b = 12
Equation: x²/25 – y²/144 = 1

Example 2: Eccentricity

Find eccentricity of hyperbola x²/9 – y²/16 = 1.

Solution:
a² = 9, b² = 16, c² = a² + b² = 25 → c = 5
Eccentricity = c/a = 5/3 > 1

Example 3: Tangent

Find equation of tangent at point (x₁, y₁) = (a secθ, b tanθ).

Solution:
(xx₁)/a² – (yy₁)/b² = 1 → parametric form gives tangent directly.

Example 4: Asymptotes

Find asymptotes of hyperbola x²/25 – y²/9 = 1.

Solution:
y = ±(b/a)x = ±(3/5)x

Example 5: Conjugate Hyperbola

Find conjugate of x²/36 – y²/25 = 1.

Solution:
y²/25 – x²/36 = 1

Applications of Hyperbola

1. Astronomy: Some comets and celestial bodies follow hyperbolic orbits.
2. Physics: Used in designing telescopes and antennas.
3. Engineering: Navigation systems and radar tracking.
4. Exams: Problems on tangents, normals, asymptotes, eccentricity.

Common Mistakes

• Confusing ellipse and hyperbola equations.
• Forgetting relation c² = a² + b² (not minus).
• Mixing asymptote slopes with ellipse axis ratios.
• Wrong orientation (x vs y axis transverse).

Exam Weightage

• CBSE Boards: 6–8 marks (general equation and tangent problems).
• JEE Main: 1–2 questions (~8 marks, often tangent/asymptote).
• JEE Advanced: Conceptual parametric problems (~4 marks).
• KCET/COMEDK: 2–3 formula-based MCQs (~6–9 marks).

Practice Problems

1. Find equation of hyperbola with vertices (±a, 0) and eccentricity e. 
2. Write asymptotes of hyperbola x²/49 – y²/36 = 1. 
3. Find equation of tangent at point (5, 4) on hyperbola x²/25 – y²/16 = 1. 
4. Find eccentricity of hyperbola y²/9 – x²/16 = 1. 
5. Derive parametric representation of x²/a² – y²/b² = 1. 
6. Show that the conjugate hyperbola of x²/25 – y²/9 = 1 is y²/9 – x²/25 = 1. 
7. Find coordinates of foci of x²/100 – y²/64 = 1. 
8. Prove that product of asymptote slopes = –1. 
9. Find equation of normal at (a secθ, b tanθ). 
10. Show that hyperbola reduces to pair of straight lines when constant → 0. 

FAQs

Q1. How is hyperbola different from ellipse?
Ellipse: sum of distances from foci constant.
Hyperbola: difference of distances constant.

Q2. What is the eccentricity of hyperbola?
e = c/a, where c² = a² + b², e > 1.

Q3. What are asymptotes of hyperbola?
Lines y = ±(b/a)x that branches approach at infinity.

Q4. What is a conjugate hyperbola?
If one hyperbola has a transverse axis along the x-axis, the conjugate has it along the y-axis.

Q5. Where do hyperbolas occur in nature?
Orbits of comets, navigation signals, radar paths.

Conclusion

The hyperbola is the final conic section that completes the study of circles, ellipses, and parabolas. Defined as the locus of points with constant difference of distances from foci, the hyperbola is unique with its open structure, asymptotes, and eccentricity > 1.

We studied its standard and general equations, properties, tangents, normals, asymptotes, parametric representation, and conjugate hyperbola.

For JEE, KCET, COMEDK, and Boards, mastering hyperbola is crucial, especially for tangent, normal, and asymptote-related problems. Its wide real-world applications in astronomy, optics, and engineering make it a mathematically and scientifically rich concept.