Introduction
Probability is one of the most fascinating areas of mathematics because it connects real-world uncertainty with precise mathematical reasoning. For JEE aspirants, mastering the axiomatic approach to probability is essential—not just for solving direct questions but also for applying probability to advanced concepts like random variables, Bayes' theorem, and combinatorial analysis.
The axiomatic approach, developed by Andrey Kolmogorov in 1933, brought rigor and logical consistency to probability theory. Instead of relying on intuition or equally likely outcomes, this approach defines probability through a set of axioms (rules) that every probability measure must follow. Using these axioms, all properties of probability can be derived logically.
Why the Axiomatic Approach Matters for JEE
In the JEE syllabus (both Main and Advanced), the axiomatic approach forms the foundation for advanced probability problems. Questions often test:
- Understanding and application of the three axioms.
- Derivation and use of properties such as P(A′) = 1 − P(A), P(∅) = 0, and P(A ∪ B) = P(A) + P(B) − P(A ∩ B).
- Handling mutually exclusive and independent events through axiomatic reasoning.
- Conditional probability and Bayes' theorem, which build upon these axioms.
Weightage:
JEE Main: 2–3 questions (typically 8–12 marks).
JEE Advanced: 1–2 questions (conceptual, multi-step, or involving combinatorial probability).
The Axiomatic Framework
1. Sample Space and Events
Every probability problem begins with defining a sample space S — the set of all possible outcomes of an experiment. An event is a subset of this sample space.
Example:
If a die is rolled,
S =
A = (even numbers)
We define a probability function P that assigns to each event A a real number P(A) representing the likelihood of that event.
Kolmogorov's Three Axioms of Probability
Axiom 1: Non-Negativity
P(A) ≥ 0 for all A ⊆ S
This means the probability of any event cannot be negative.
Example:
It is meaningless to say the probability of getting a head in a coin toss is −0.5. Hence, all probabilities are non-negative.
Axiom 2: Normalization (Total Probability)
P(S) = 1
The total probability of the sample space (the certainty of some outcome occurring) is 1.
Example:
In a die roll, P(S) = P() = 1 because one of these outcomes must occur.
Axiom 3: Additivity (Finite Additivity)
For any two mutually exclusive events A and B (i.e., A ∩ B = ∅),
P(A ∪ B) = P(A) + P(B)
This property can be extended to more than two events:
P(A₁ ∪ A₂ ∪ A₃ ∪ …) = ΣP(Aᵢ)
if all Aᵢ are mutually exclusive.
Example:
In a die roll,
A = , B =
A ∩ B = ∅ and
P(A ∪ B) = P(A) + P(B) = 2/6 + 2/6 = 4/6
Derived Properties from the Axioms
The beauty of the axiomatic approach is that every property of probability can be derived logically from these three rules.
- Property: P(∅) = 0
From Axiom 2: P(S) = 1.
Let A = S and B = ∅.
Since A and B are mutually exclusive,
P(S ∪ ∅) = P(S) + P(∅).
But S ∪ ∅ = S, so
P(S) = P(S) + P(∅).
Subtracting P(S) from both sides gives P(∅) = 0. - Property: P(A′) = 1 − P(A)
Here, A′ denotes the complement of A (the outcomes where A does not occur).
Since S = A ∪ A′ and A ∩ A′ = ∅,
P(S) = P(A) + P(A′).
Using Axiom 2 (P(S) = 1):
1 = P(A) + P(A′), hence P(A′) = 1 − P(A). - Property: 0 ≤ P(A) ≤ 1
From Axiom 1 and Axiom 2:
P(A) ≥ 0 and P(A) ≤ P(S) = 1.
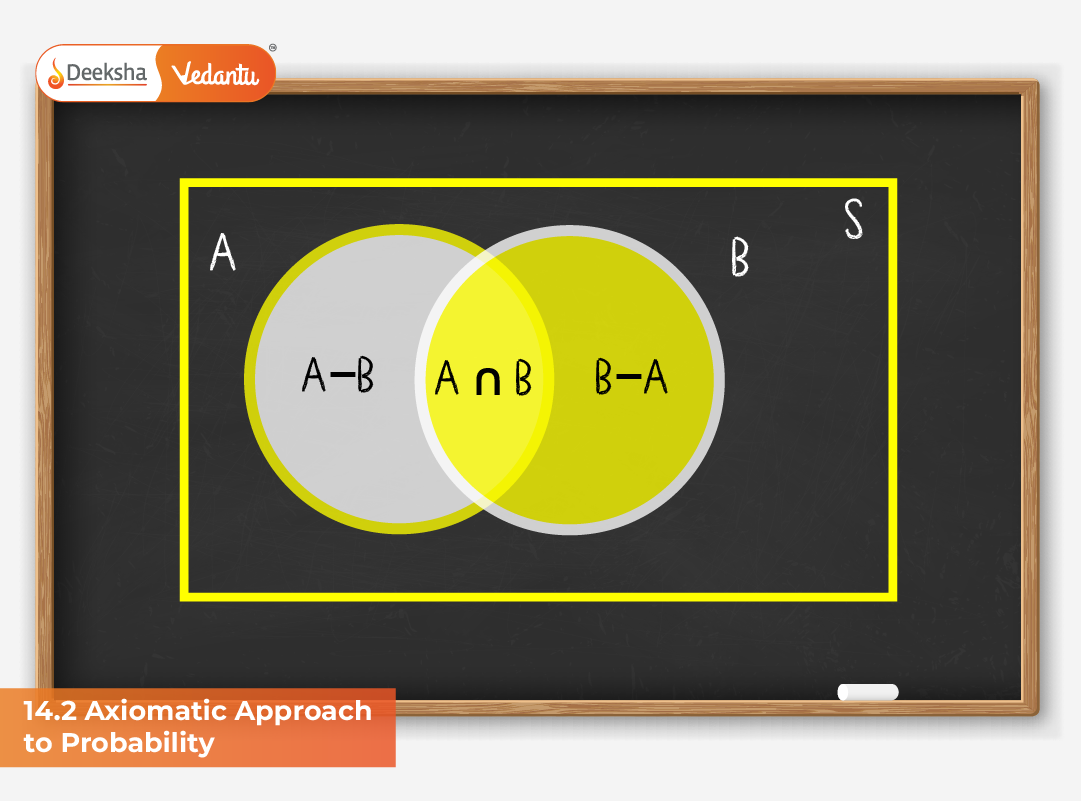
Thus, 0 ≤ P(A) ≤ 1. - Property: P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
If A and B are not mutually exclusive,
P(A ∪ B) = P(A) + P(B) − P(A ∩ B).
This avoids double-counting the intersection. - Property: For Disjoint Events
If A₁, A₂, …, Aₙ are mutually exclusive, then
P(A₁ ∪ A₂ ∪ … ∪ Aₙ) = ΣP(Aᵢ). - Property: Monotonicity
If A ⊆ B, then P(A) ≤ P(B).
Since B = A ∪ (B − A) and A ∩ (B − A) = ∅,
P(B) = P(A) + P(B − A), hence P(B) ≥ P(A). - Property: Inclusion–Exclusion Principle
For three events A, B, and C:
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) − P(A ∩ B) − P(B ∩ C) − P(C ∩ A) + P(A ∩ B ∩ C).
This is often used in complex JEE problems involving overlapping events.
Advanced Applications in JEE Context
- Independent vs. Mutually Exclusive Events
- Mutually exclusive: A ∩ B = ∅ ⇒ P(A ∩ B) = 0
- Independent: P(A ∩ B) = P(A) × P(B)
Example:
If you roll a die:
A = "Even number" → P(A) = 3/6 = 1/2
B = "Number > 4" → P(B) = 2/6 = 1/3
P(A ∩ B) = 1/6
Since 1/6 = (1/2) × (1/3), A and B are independent.
- Law of Total Probability
If A₁, A₂, …, Aₙ form a partition of the sample space, then
P(B) = Σ P(Aᵢ) × P(B | Aᵢ).
This law is often used in JEE Advanced. - Bayes' Theorem (Based on Axioms)
P(Aᵢ | B) = [P(Aᵢ) × P(B | Aᵢ)] / Σ[P(Aⱼ) × P(B | Aⱼ)].
It is derived directly from the axiomatic definition of conditional probability.
JEE Sample Problems
Problem 1:
If P(A) = 0.4, P(B) = 0.5, and P(A ∪ B) = 0.7, find P(A ∩ B).
Solution:
P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
0.7 = 0.4 + 0.5 − P(A ∩ B)
P(A ∩ B) = 0.2
Problem 2:
If P(A) = 0.6, find P(A′).
P(A′) = 1 − P(A) = 0.4
Problem 3:
A card is drawn from a deck. Let
A: card is red, B: card is a king.
P(A) = 26/52 = 1/2
P(B) = 4/52 = 1/13
P(A ∩ B) = 2/52 = 1/26
P(A ∪ B) = 1/2 + 1/13 − 1/26 = 15/26
Problem 4 (Advanced):
Events A and B are such that P(A) = 0.7, P(B) = 0.6, P(A ∩ B) = 0.5.
Find P(A′ ∪ B′).
P(A′ ∪ B′) = 1 − P(A ∩ B) = 1 − 0.5 = 0.5
Marks Distribution in JEE
| Topic | JEE Main (Marks) | JEE Advanced (Marks) | Difficulty |
| Axioms & Definitions | 4 | 0–3 | Easy |
| Derived Properties | 4–8 | 3–6 | Medium |
| Conditional Probability | 8 | 6 | Moderate |
| Bayes' Theorem | 4 | 6 | Moderate |
| Total Probability & Combinations | 4 | 8 | Hard |
Common JEE Mistakes
- Confusing mutual exclusivity with independence.
- Forgetting that P(S) = 1 even in conditional problems.
- Neglecting overlap between events before applying additivity.
- Using P(A ∪ B) = P(A) + P(B) without subtracting P(A ∩ B).
FAQs
Q1. What is the main idea behind the axiomatic approach?
It defines probability through mathematical rules (axioms) rather than intuition. These axioms ensure all derived results are logically consistent and universally applicable.
Q2. How many axioms are there in probability?
Three: non-negativity, normalization, and additivity. All other properties stem from these.
Q3. Is P(∅) = 0 an axiom or derived?
It is derived from the three axioms using additivity and normalization.
Q4. What is the most important derived property for JEE?
The formula P(A ∪ B) = P(A) + P(B) − P(A ∩ B) is frequently used in JEE questions.
Q5. How is the axiomatic approach used in advanced probability?
It provides the foundation for conditional probability, independence, Bayes' theorem, and random variables.
Conclusion
The axiomatic approach to probability is the cornerstone of modern probability theory. For JEE aspirants, it is not only about memorizing the three axioms but understanding how every probability rule emerges logically from them. By mastering these foundational ideas—especially derived properties and logical reasoning—students can solve even the most challenging probability questions in JEE with confidence.






Get Social