Mathematics is a structured language built on logical relationships and well-defined principles. At the core of this language lie two important foundational concepts: sets and rational numbers. These topics are not only crucial for mastering Class 10 math but also serve as the gateway to understanding higher-level topics like algebra, probability, and number theory. They lay the groundwork for problem-solving, analytical reasoning, and structured thinking across disciplines.
This comprehensive guide takes a closer look at what sets and rational numbers really are, their classifications, properties, operations, and how they integrate with broader mathematical systems like the real number system. We’ll also explore their applications and visualization through diagrams such as Venn diagrams and number lines.
What is a Set?
A set is essentially a collection of well-defined and distinct objects, considered as a single entity. These objects are called elements or members of the set. Sets allow us to group, classify, and analyze objects in a logical and mathematical way.
For example:
- Set A = {2, 4, 6, 8} – the even numbers less than 10
- Set B = {a, e, i, o, u} – the vowels in the English alphabet
Sets can be represented in different formats:
- Roster form: Elements are listed explicitly, e.g.,
- Set-builder form: A rule defines the elements, e.g.,
This makes sets highly versatile in various math problems, especially those involving group theory and classification.
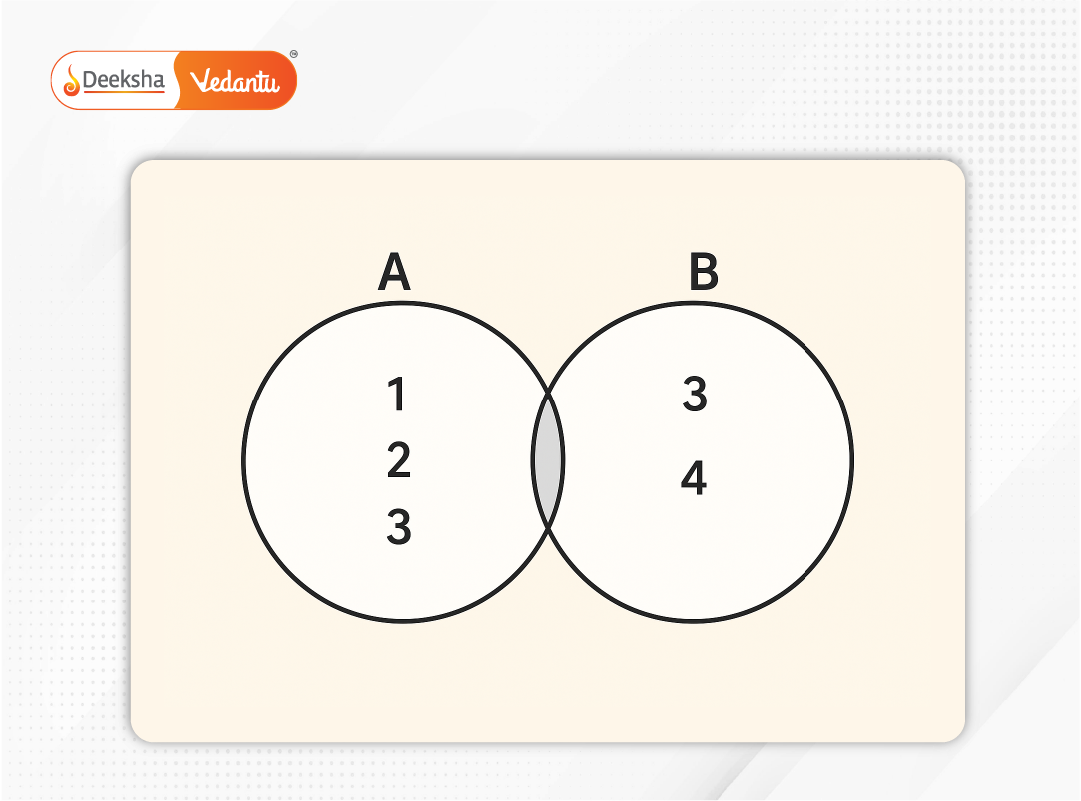
Types of Sets
Sets come in various types depending on their structure and number of elements. Understanding these categories enables more accurate operations and better analysis:
- Empty Set (Null Set): Contains no elements. Example:
- Finite Set: Has a limited number of elements. Example:
- Infinite Set: Has unlimited or uncountable elements. Example:
- Subset:
if all elements of A are also elements of B
- Proper Subset:
implies A is a subset but not equal to B
- Universal Set: Contains all the elements under discussion
- Power Set: The set of all subsets of a given set. If a set has n elements, the power set has
subsets
These types play a key role in areas like database design, logic gates, and even AI classification models.
Venn Diagrams and Set Operations
Venn diagrams help visualize the relationships between two or more sets using overlapping circles. This makes understanding concepts like union, intersection, and complement far easier.
Common operations include:
- Union (A ∪ B): All elements in A, B, or both
- Intersection (A ∩ B): Only the elements common to both sets
- Difference (A – B): Elements in A but not in B
- Complement (A’): All elements not in A, relative to the universal set
These operations are essential for logical reasoning and are widely used in computer science and data analytics.
Related Concept: Rational Numbers

What are Rational Numbers?
A rational number is any number that can be expressed in the form pq\frac{p}{q}, where pp and qq are integers and q≠0q \neq 0. These numbers are extremely versatile and include:
- Natural numbers:
- Whole numbers:
- Integers:
- Fractions:
- Decimals: Both terminating and recurring decimals
On the other hand, irrational numbers like or
cannot be written as
. Understanding this helps classify numbers properly within the number system.
Operations on Rational Numbers
Rational numbers are closed under all four basic operations—addition, subtraction, multiplication, and division (except by zero). Here are the formulas:
- Addition:
- Subtraction:
- Multiplication:
- Division:
These operations obey:
- Commutative Law:
- Associative Law:
- Distributive Law:
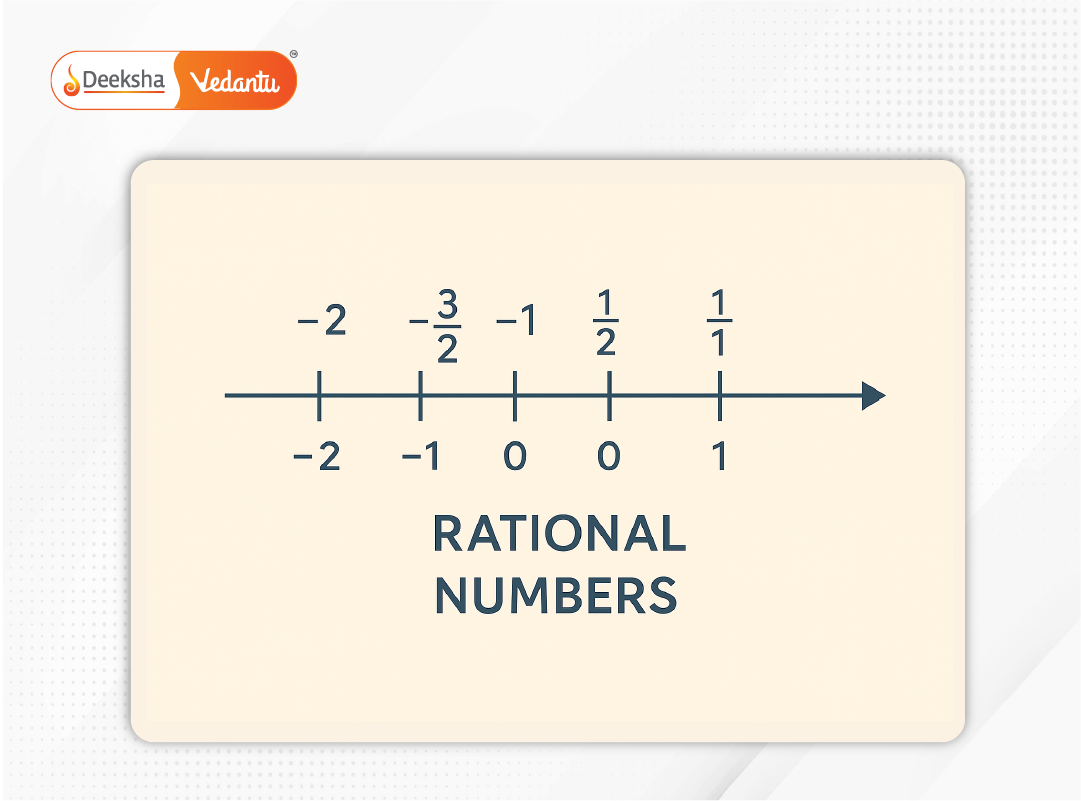
Rational Numbers in the Real Number System
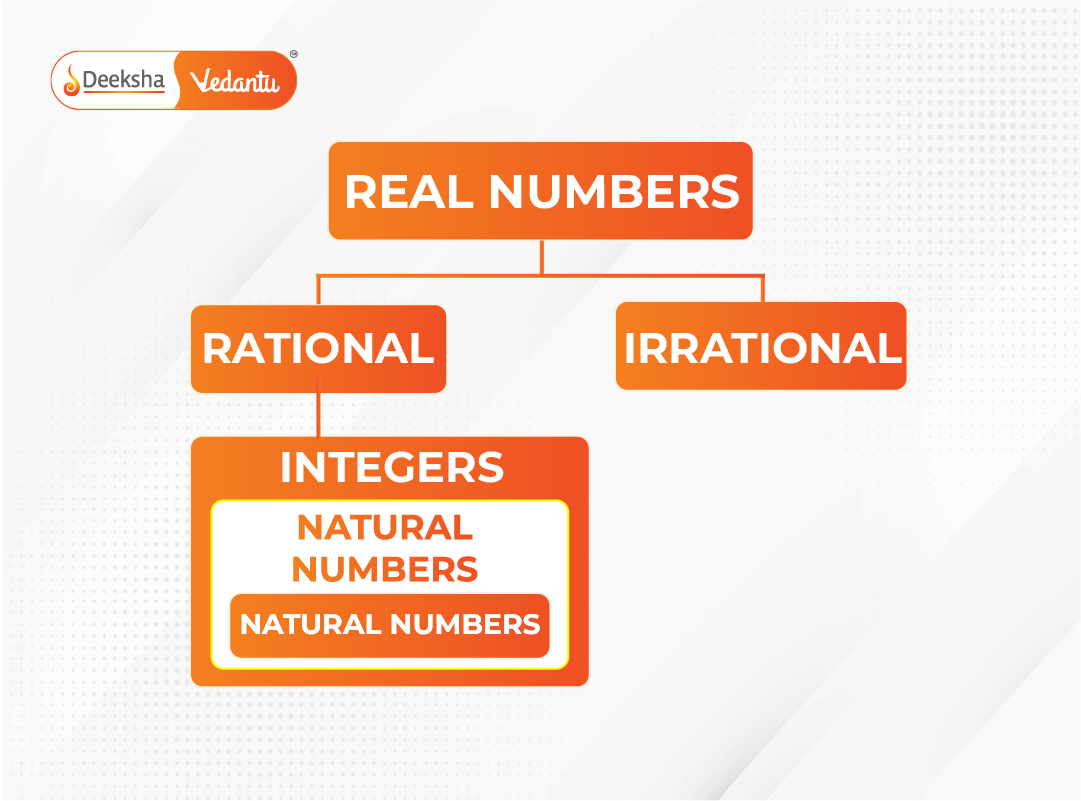
Rational numbers belong to the real number system, which includes both rational and irrational numbers. This classification is important in:
- Solving quadratic and polynomial equations
- Representing real-world measurements
- Performing accurate scientific calculations
Real numbers can be graphically represented on a number line. Rational numbers form precise, countable points, while irrational numbers fill the continuous gaps.
Don’t Miss: Fundamental Theorem of Arithmetic
Visualizing Rational and Irrational Numbers
Visualization enhances understanding. Tools like:
- Number lines: Help in plotting fractions and decimals
- Venn diagrams: Illustrate set relationships
- Bar and pie charts: Show proportional data
These tools improve retention and conceptual clarity.
Explore: Revisiting Irrational Numbers
Real-World Applications of Sets and Rational Numbers
Understanding sets and rational numbers is not just for exams—it has real-life significance:
- Computer programming: Sets are used in algorithms and data structures
- Business analytics: Rational numbers assist in financial forecasts and pricing
- Science: Measurements and results are often rational approximations
- Education: Classification of student data using sets
- Medical science: Dosage and statistical analysis use rational values
These concepts enhance logical thinking and are foundational for various career paths.
FAQs on Sets and Rational Numbers
1. What is the definition of a set in math?
A set is a well-defined collection of distinct elements, written using curly brackets {}.
2. What is a rational number?
A rational number is any number that can be written in the form .
3. How do you add rational numbers?
By finding a common denominator, adjusting the numerators, adding them, and simplifying the result.
4. How are sets used in real life?
Sets are used in data classification, programming logic, and organizing information.
5. Are all decimals rational numbers?
No. Only terminating or repeating decimals are rational. Others, like , are irrational.
Conclusion
Understanding the concepts of sets and rational numbers is not just crucial for academic success but also forms a solid foundation for future learning. These mathematical tools are used extensively across disciplines like computer science, finance, and engineering. With regular practice, visual aids, and real-world application, students can master these concepts and build confidence in mathematics.
So continue to explore problems, create your own sets, and apply operations on rational numbers to develop deep mathematical thinking. With a strong foundation, you’ll be prepared for whatever mathematical challenge comes next!
Table of Contents












Get Social