Introduction to Arithmetic Progressions

Arithmetic Progressions (AP) are one of the most important and foundational topics in Class 10 mathematics. Whether you’re solving problems related to daily life, physics, or competitive exams, the concept of AP makes repeated appearances. Understanding the basics of AP helps students build strong problem-solving abilities and develop pattern recognition.

In this comprehensive guide, we will explore what an AP is, how to calculate its nth term and sum, the most important formulas you need to know, the various types of arithmetic sequences, and their practical applications in real life. We will also discuss how AP is connected to other mathematical topics, present real-life examples, and answer some of the most commonly asked questions through a helpful FAQ section.

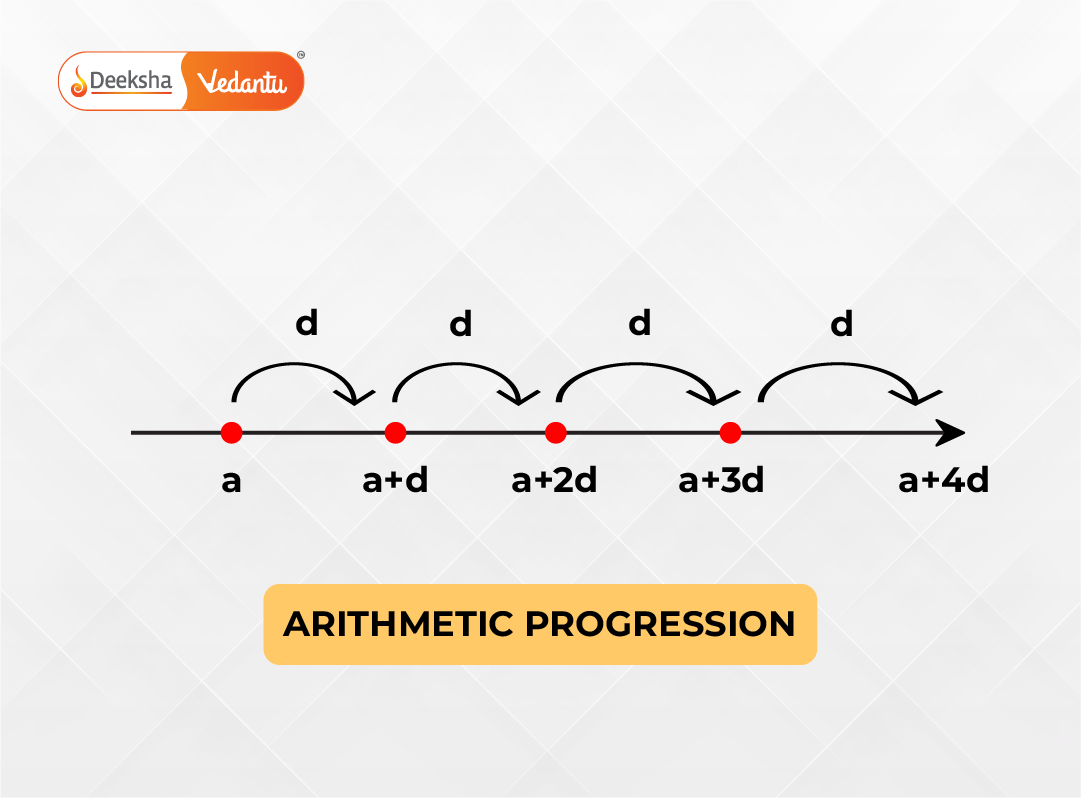
What is an Arithmetic Progression (AP)?

An Arithmetic Progression is a sequence of numbers in which the difference between any two successive terms is always the same. This consistent value is known as the common difference (d), and it forms the basis of the entire progression.

For example, the sequence:

is an arithmetic progression where the common difference is . Each new term is found by adding the common difference to the term before it.

This principle applies to both increasing and decreasing sequences. A decreasing AP might look like:

where

Learn more: Introduction to Arithmetic Progressions

General Form of an AP

The general representation of an AP allows you to visualize any arithmetic sequence in a compact mathematical format:

Where:

• is the first term
• is the common difference
• represents the terms at consistent intervals

Understanding this structure helps you quickly identify terms and derive relationships within the sequence.

Formula for the nth Term of an AP

The formula to calculate the nth term of an AP is fundamental and widely used:

Where:

• is the nth term
• is the first term
• is the common difference
• is the position of the term in the sequence

Using this formula, you can find any term in the sequence, even without knowing all the terms before it. It’s especially helpful for solving problems efficiently during exams.

Explore: nth Term of an AP

Sum of the First n Terms of an AP

When you’re asked to find the sum of a certain number of terms in an AP, use these two key formulas:

or,

Where:

• is the sum of the first n terms
• is the first term
• is the last term
• is the number of terms 

These formulas are crucial when working with long sequences where adding each term manually is inefficient. They also appear frequently in both board exams and competitive exams.

Check out: Sum of First n Terms of an AP

Applications of AP in Real Life

Arithmetic Progressions are not just textbook theory – they are highly applicable in practical scenarios. Here are some everyday examples:

• Bank deposits that increase by a fixed amount every month
• Seating arrangements in auditoriums or stadiums, where each row adds a fixed number of seats
• Salary increments that follow a steady annual or monthly raise
• Saving patterns such as saving an additional ₹100 each month
• Scheduling bus or train departures at regular time intervals

Recognizing these real-life patterns as APs helps you plan better and apply mathematical thinking in daily activities.

Common Pitfalls and Tips

Students often make some typical mistakes while working with APs. Here are a few tips to avoid them:

• Always confirm that a sequence has a constant difference before assuming it’s an AP
• Don’t confuse AP with geometric progression (GP), which involves multiplication rather than addition
• Use the nth term formula instead of manually extending the sequence
• When the question is lengthy, organize known values clearly: aa, dd, ,
• Remember that APs can have negative or zero common differences too

Connecting AP to Other Math Topics

The concept of AP serves as a strong foundation for exploring other mathematical domains. In particular:

• Quadratic Equations: Word problems involving AP often lead to quadratic equations that need to be solved
• Graphs: Graphical representation of an AP forms a straight line when plotted, as the change is linear
• Algebraic Patterns: Patterns in algebra often follow an AP structure, especially in problems involving consecutive terms

Explore: Introduction to Quadratic Equations

Related: Solving Quadratics by Factorisation

FAQs: Arithmetic Progression Class 10

1. What is the formula for the nth term of an AP?

This formula helps find any term in the sequence without listing all the terms.

2. How do you find the sum of an AP?

Use:

depending on the given information.

3. Can AP have a negative common difference?

Yes! An AP with a negative dd decreases with each term. For example:

4. Is Arithmetic Progression used in real life?

Definitely! APs are used in saving schemes, scheduling, architectural design, and many routine tasks that involve steady changes.

5. What happens if the common difference is zero?

All terms in the AP are the same. It’s called a constant sequence:

Conclusion

Mastering the concept of Arithmetic Progressions is essential for Class 10 students aiming to perform well in math exams and competitive tests. With a strong understanding of AP formulas, the nth term, and sum calculations, students gain both theoretical and practical mathematical fluency.

Whether you are preparing for a class test, board exam, or just trying to improve your logical reasoning, AP is one of the easiest and most logical topics in the math curriculum. Remember to practice regularly, solve word problems from different contexts, and revise the formulas frequently.

With consistent effort and understanding, AP will become one of your strongest and most reliable tools in mathematics!