Polynomials form a foundational pillar in algebra and appear extensively in Class 10 mathematics. These expressions consist of variables and constants, linked together by mathematical operations such as addition, subtraction, multiplication, and non-negative integer exponents. Mastery over polynomials is crucial not just for acing school-level exams but also for laying the groundwork for advanced mathematical topics and practical problem-solving in the real world.

Whether you’re dealing with equations in physics or analyzing patterns in economics, polynomials make their appearance. This guide will walk you through the essential concepts – what polynomials are, the various types you’ll encounter, how to calculate their zeroes, and how to factorise them efficiently. We’ll also highlight real-world applications, connect you to additional helpful resources, and clarify common doubts with an FAQ section.

What Are Polynomials?

A polynomial is a mathematical expression made up of variables (also called indeterminates), coefficients, and operations involving only non-negative integer exponents. These expressions are usually written in terms of a single variable (like x), but they can also involve multiple variables.

For example:

\boldsymbol{3x^2 - 5x + 2}

This expression has three terms and the highest power of x is 2, making it a quadratic polynomial. Each part like \boldsymbol{3x^2}, \boldsymbol{-5x}, and \boldsymbol{22} is called a term.

The standard form of a polynomial in one variable looks like:

\boldsymbol{a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x + a_0}

Here, \boldsymbol{a_n, a_{n-1}, \dots, a_0} are real number coefficients, and nn is a non-negative integer representing the degree.

Explore: Introduction to Polynomials

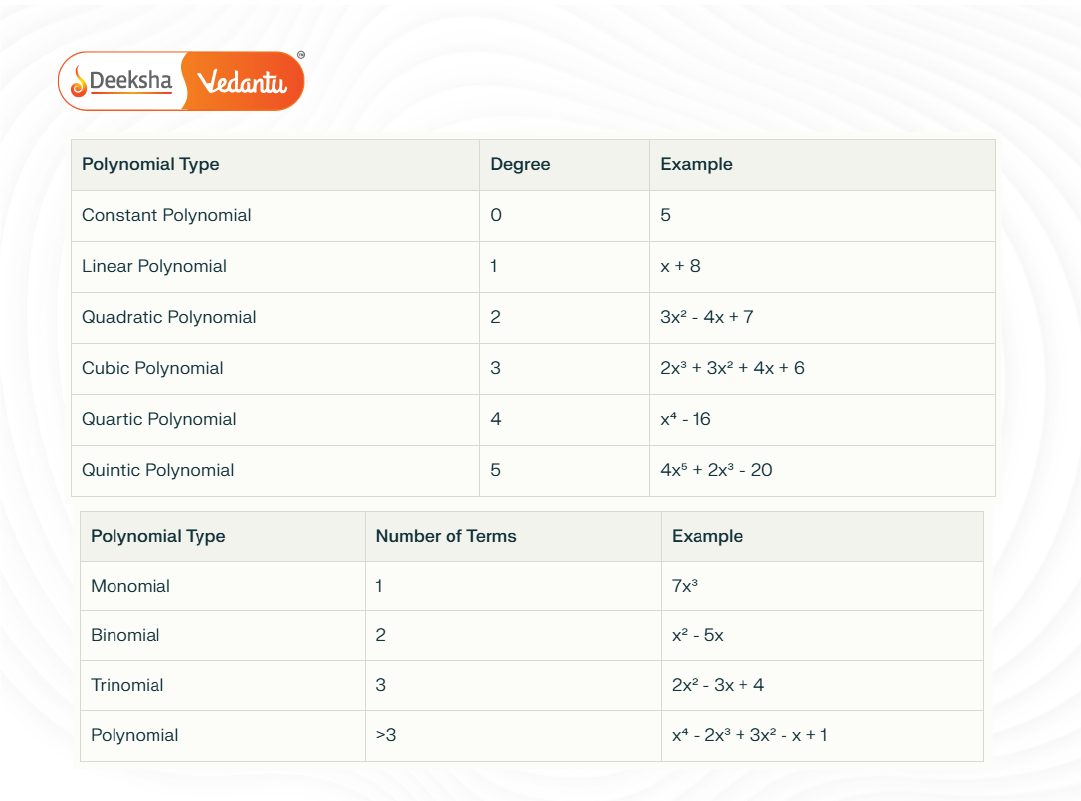
Types of Polynomials

Polynomials can be categorised in two primary ways: by the number of terms they contain and by the degree (highest exponent) of the polynomial.

Based on Number of Terms

  • Monomial: Consists of only one term. Example: \boldsymbol{4x}
  • Binomial: Contains two terms. Example: \boldsymbol{3x + 7}
  • Trinomial: Made up of three terms. Example: \boldsymbol{2x + 3}
  • Multinomial: Includes more than three terms, though rarely used in basic discussions.

Based on Degree

  • Constant Polynomial: Degree 0. Example: \boldsymbol{77}
  • Linear Polynomial: Degree 1. Example: \boldsymbol{2x + 3}
  • Quadratic Polynomial: Degree 2. Example: \boldsymbol{x^2 + 4x + 4}
  • Cubic Polynomial: Degree 3. Example: \boldsymbol{x^3 - 3x^2 + 2}
  • Quartic Polynomial: Degree 4. Example: \boldsymbol{x^4 + 2x^3 - x + 1}

Identifying the type of polynomial helps you choose appropriate methods for solving or simplifying the expression.

Also read: Real Numbers

Check out: Revisiting Irrational Numbers

Chart showing classification of polynomials by degree and terms with examples

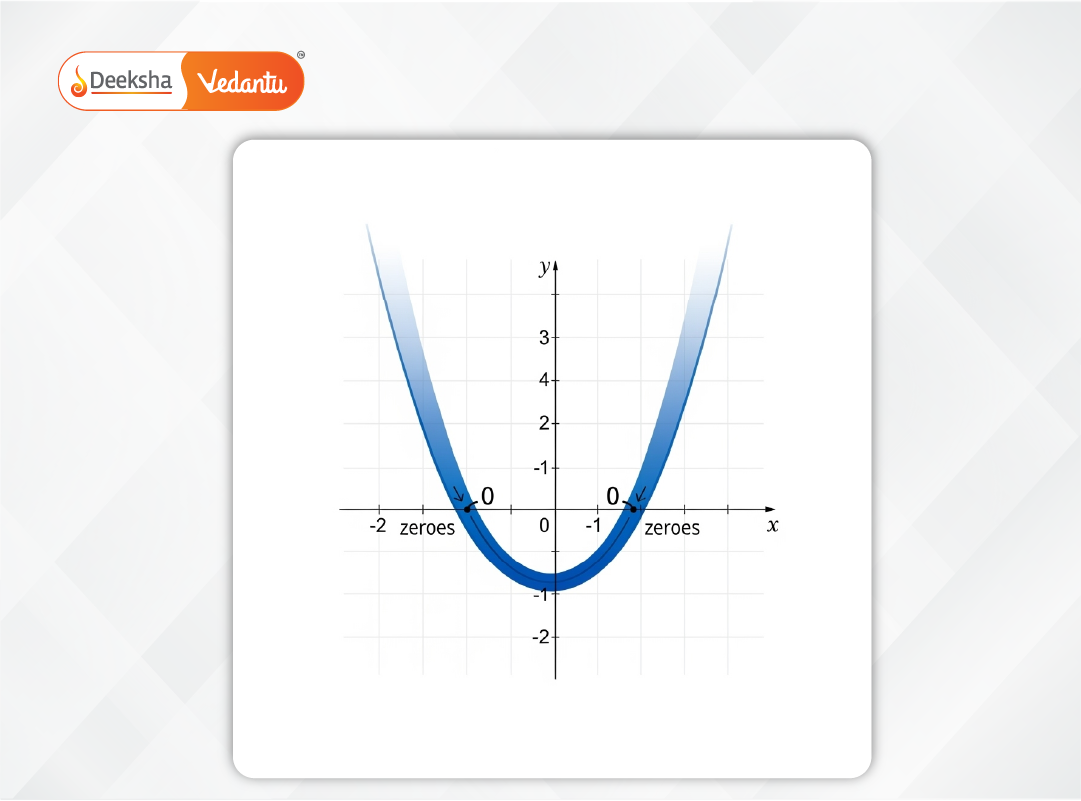
Zeroes of a Polynomial

The zeroes or roots of a polynomial are the values of the variable that satisfy the condition \boldsymbol{f(x) = 0}. They are the x-values where the polynomial graph intersects the x-axis.

For example, if:

\boldsymbol{f(x) = x^2 - 5x + 6}

then the zeroes are \boldsymbol{x = 2} and \boldsymbol{x = 3} because:

\boldsymbol{f(2) = 0} and \boldsymbol{f(3) = 0}

These zeroes are essential in graphing, solving equations, and factorising polynomials.

Explore: Geometrical Meaning of Zeroes

Graph of a parabola showing its zeroes where the curve meets the x-axis

Relationship Between Zeroes and Coefficients

Understanding how the zeroes of a polynomial relate to its coefficients is a powerful tool, especially for quadratic polynomials.

For a quadratic polynomial:

\boldsymbol{ax^2 + bx + c}

Let the zeroes be \boldsymbol{\alpha} and \boldsymbol{\beta}. Then:

  • Sum of zeroes: \boldsymbol{\alpha + \beta = -\frac{b}{a}}
  • Product of zeroes: \boldsymbol{\alpha \cdot \beta = \frac{c}{a}}

This relationship helps reconstruct a polynomial when the zeroes are known and can simplify many exam problems.

Learn: Zeroes and Coefficients

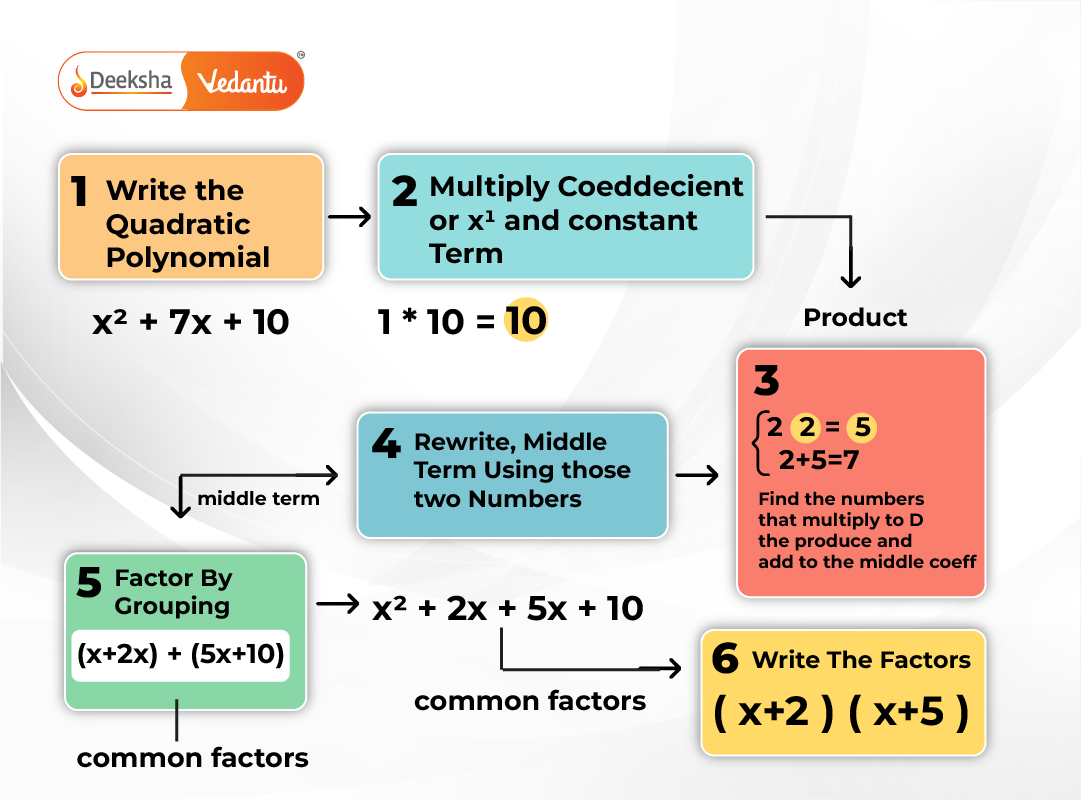
Factorisation of Polynomials

Factorising a polynomial means rewriting it as a product of its factors. This process is crucial for simplifying expressions and solving equations. Some popular methods include:

  • Taking out common factors
  • Using algebraic identities: e.g. \boldsymbol{(a + b)^2 = a^2 + 2ab + b^2}
  • Splitting the middle term: Common for quadratic polynomials
  • Factor Theorem and Remainder Theorem

Once the zeroes of a polynomial are known, factorisation becomes even easier. Practice with different techniques helps you gain flexibility in solving a variety of problems.

Step-by-step breakdown of polynomial factorisation using middle-term splitting

Importance of Polynomials in Real Life

Polynomials aren’t just theoretical concepts – they’re used across many fields:

  • Physics: Modeling motion, forces, and wave patterns
  • Economics: Creating supply, demand, and cost functions
  • Engineering: Structural designs and stress-strain analysis
  • Computer Graphics: Designing animations and rendering curves
  • Machine Learning: Polynomial regression models

Understanding polynomials improves analytical thinking, pattern recognition, and your ability to solve complex problems efficiently.

FAQs: Polynomials Class 10

1. What is a polynomial?

A polynomial is an algebraic expression consisting of variables and constants combined using addition, subtraction, multiplication, and non-negative powers.

2. How are polynomials classified?

Polynomials can be classified based on the number of terms (monomial, binomial, trinomial) and the degree (linear, quadratic, cubic, etc.).

3. What are the zeroes of a polynomial?

They are the values of the variable that make the polynomial equal to zero. These are also the points where the polynomial graph crosses the x-axis.

4. Why is factorisation useful?

Factorisation simplifies solving polynomial equations and is essential for higher-level math topics like calculus and algebraic geometry.

5. How are polynomials used in the real world?

They’re used in physics, computer science, economics, and engineering to model and solve real-life problems.

Conclusion

Polynomials are the backbone of many algebraic concepts in mathematics. From identifying degrees and terms to understanding zeroes and factorisation techniques, this topic holds great significance in Class 10 and beyond. With clear definitions, solved examples, and practical applications, students can develop both computational and conceptual skills.

As you prepare for your exams, don’t just memorize formulas – understand how and why they work. Use this guide to revisit key points and explore the interlinked lessons to strengthen your understanding.

With consistent practice, polynomials can become one of the easiest and most scoring chapters in your math curriculum.

pu-admission
take-dsat

Join Deeksha Vedantu

> PU + Competitive Exam CoachingPreferred Choice For Toppers25+ Years of Academic Excellence70k+ Success Stories

Table of Contents

blog-banner-dsat

Continue Reading

  • Understanding Sets and Rational Numbers

    Understanding Sets and Rational Numbers

  • Earthquake Safety and Seismic Design

    Earthquake Safety and Seismic Design

  • Introduction to Arithmetic Progressions

    Introduction to Arithmetic Progressions

  • Getting Started with Polynomials

    Getting Started with Polynomials

  • Biology of the Nervous System

    Biology of the Nervous System

  • Real-Life Applications of Reflection and Refraction

    Real-Life Applications of Reflection and Refraction

  • Periodicity in the Periodic Table

    Periodicity in the Periodic Table

  • Simple Machines and Physics Behind Them

    Simple Machines and Physics Behind Them