Trigonometric Ratios of Some Specific Angles

Overview of Trigonometric Ratios for Specific Angles

Trigonometric ratios for specific angles— $\boldsymbol{0^\circ}$ , $\boldsymbol{30^\circ}$ , $\boldsymbol{45^\circ}$ , $\boldsymbol{60^\circ}$ , and $\boldsymbol{90^\circ}$ —are essential in trigonometry. These angles, often referred to as standard angles, have predefined trigonometric values that simplify calculations. Memorizing these ratios allows for efficient problem-solving in trigonometry without requiring a calculator.

Trigonometric ratios for these angles are derived from geometric principles, such as properties of equilateral triangles, isosceles triangles, and the Pythagorean theorem.

Why These Angles Are Considered Standard

Symmetry and Simplicity:
- These angles appear naturally in symmetrical geometric shapes like equilateral and isosceles right triangles.
- The trigonometric ratios for these angles follow specific patterns, making them easy to remember and compute.
Frequent Occurrence in Applications:
- These angles commonly occur in real-world problems, such as calculating heights, distances, slopes, and angles of elevation or depression.
- They are also critical in fields like physics (wave motion, projectile motion) and engineering (design and architecture).
Geometric Foundation:
- $\boldsymbol{30^\circ}$ and $\boldsymbol{60^\circ}$ : Derived from dividing an equilateral triangle into two right triangles.
- $\boldsymbol{45^\circ}$ : Found in isosceles right triangles ( $\boldsymbol{45^\circ - 45^\circ - 90^\circ}$ ).
- $\boldsymbol{0^\circ}$ and $\boldsymbol{90^\circ}$ : Represent extreme cases where the angle collapses to a line or a vertical, respectively.

Trigonometric Ratios for Standard Angles

Key Angles

The key angles in trigonometry are:
$\boldsymbol{0^\circ}$ , $\boldsymbol{30^\circ}$ , $\boldsymbol{45^\circ}$ , $\boldsymbol{60^\circ}$ , and $\boldsymbol{90^\circ}$ .
These angles are used frequently in solving trigonometric problems due to their predictable and simplified trigonometric ratios.

Table of Trigonometric Ratios

$\boldsymbol{\theta}$ (Angle)	$\boldsymbol{\sin \theta}$	$\boldsymbol{\cos \theta}$	$\boldsymbol{\tan \theta}$	$\boldsymbol{\csc \theta}$	$\boldsymbol{\sec \theta}$	$\boldsymbol{\cot \theta}$
$\boldsymbol{0^\circ}$	$\boldsymbol{0}$	$\boldsymbol{1}$	$\boldsymbol{0}$	$\boldsymbol{\text{Undefined}}$	$\boldsymbol{1}$	$\boldsymbol{\text{Undefined}}$
$\boldsymbol{30^\circ}$	$\displaystyle\boldsymbol{\frac{1}{2}}$	$\displaystyle\boldsymbol{\frac{\sqrt{3}}{2}}$	$\displaystyle\boldsymbol{\frac{1}{\sqrt{3}}}$	$\boldsymbol{2}$	$\displaystyle\boldsymbol{\frac{2}{\sqrt{3}}}$	$\boldsymbol{\sqrt{3}}$
$\boldsymbol{45^\circ}$	$\displaystyle\boldsymbol{\frac{1}{\sqrt{2}}}$	$\displaystyle\boldsymbol{\frac{1}{\sqrt{2}}}$	$\boldsymbol{1}$	$\boldsymbol{\sqrt{2}}$	$\boldsymbol{\sqrt{2}}$	$\boldsymbol{1}$
$\boldsymbol{60^\circ}$	$\displaystyle\boldsymbol{\frac{\sqrt{3}}{2}}$	$\displaystyle\boldsymbol{\frac{1}{2}}$	$\boldsymbol{\sqrt{3}}$	$\displaystyle\boldsymbol{\frac{2}{\sqrt{3}}}$	$\boldsymbol{2}$	$\displaystyle\boldsymbol{\frac{1}{\sqrt{3}}}$
$\boldsymbol{90^\circ}$	$\boldsymbol{1}$	$\boldsymbol{0}$	$\boldsymbol{\text{Undefined}}$	$\boldsymbol{1}$	$\boldsymbol{\text{Undefined}}$	$\boldsymbol{0}$

Explanation of Table

$\boldsymbol{\sin \theta}$ and $\boldsymbol{\cos \theta}$ :
- These values are derived from the geometric properties of right triangles.
- $\boldsymbol{\sin \theta}$ and $\boldsymbol{\cos \theta}$ are complementary for these angles:
  $\boldsymbol{\sin \theta = \cos(90^\circ - \theta)}$ .
$\boldsymbol{\tan \theta}$ :
- $\displaystyle\boldsymbol{\tan \theta = \frac{\sin \theta}{\cos \theta}}$ .
- Undefined for $\boldsymbol{\theta = 90^\circ}$ , as $\boldsymbol{\cos \theta = 0}$ .
Reciprocal Ratios:
- $\displaystyle\boldsymbol{\csc \theta = \frac{1}{\sin \theta}}$ .
- $\displaystyle\boldsymbol{\sec \theta = \frac{1}{\cos \theta}}$ .
- $\displaystyle\boldsymbol{\cot \theta = \frac{1}{\tan \theta}}$ .

Derivation of Ratios for Specific Angles

For $\boldsymbol{45^\circ}$

Consider an Isosceles Right Triangle:
In a $\boldsymbol{45^\circ - 45^\circ - 90^\circ}$ triangle:
- The two legs are equal, and let their length be $\boldsymbol{1}$ .
- The hypotenuse is calculated using the Pythagorean theorem: $\boldsymbol{\text{Hypotenuse} = \sqrt{1^2 + 1^2} = \sqrt{2}}$
Trigonometric Ratios for $\boldsymbol{45^\circ}$ : Using the definitions of trigonometric ratios:
- $\displaystyle\boldsymbol{\sin 45^\circ = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{1}{\sqrt{2}}}$ .
- $\displaystyle\boldsymbol{\cos 45^\circ = \frac{\text{Adjacent}}{\text{Hypotenuse}} = \frac{1}{\sqrt{2}}}$ .
- $\displaystyle\boldsymbol{\tan 45^\circ = \frac{\text{Opposite}}{\text{Adjacent}} = 1}$ .

For $\boldsymbol{30^\circ}$ and $\boldsymbol{60^\circ}$

Consider an Equilateral Triangle:
- An equilateral triangle is split into two right triangles, dividing the angles as $\boldsymbol{30^\circ - 60^\circ - 90^\circ}$ .
- Let the side of the equilateral triangle be $\boldsymbol{2a}$ .
- After splitting:
  - The hypotenuse = $\boldsymbol{2a}$ .
  - The side opposite $\boldsymbol{30^\circ}$ = $\boldsymbol{a}$ .
  - The side adjacent to $\boldsymbol{30^\circ}$ = $\boldsymbol{\sqrt{3}a}$ .
Trigonometric Ratios for $\boldsymbol{30^\circ}$ : Using the definitions:
- $\displaystyle\boldsymbol{\sin 30^\circ = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{a}{2a} = \frac{1}{2}}$ .
- $\displaystyle\boldsymbol{\cos 30^\circ = \frac{\text{Adjacent}}{\text{Hypotenuse}} = \frac{\sqrt{3}a}{2a} = \frac{\sqrt{3}}{2}}$ .
- $\displaystyle\boldsymbol{\tan 30^\circ = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{a}{\sqrt{3}a} = \frac{1}{\sqrt{3}}}$ .
Trigonometric Ratios for $\boldsymbol{60^\circ}$ : Using the same triangle:
- $\displaystyle\boldsymbol{\sin 60^\circ = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{\sqrt{3}a}{2a} = \frac{\sqrt{3}}{2}}$ .
- $\displaystyle\boldsymbol{\cos 60^\circ = \frac{\text{Adjacent}}{\text{Hypotenuse}} = \frac{a}{2a} = \frac{1}{2}}$ .
- $\displaystyle\boldsymbol{\tan 60^\circ = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{\sqrt{3}a}{a} = \sqrt{3}}$ .

Summary of Ratios

For $\boldsymbol{45^\circ}$ :
$\displaystyle\boldsymbol{\sin 45^\circ = \frac{1}{\sqrt{2}}, \cos 45^\circ = \frac{1}{\sqrt{2}}, \tan 45^\circ = 1}$ .
For $\boldsymbol{30^\circ}$ :
$\displaystyle\boldsymbol{\sin 30^\circ = \frac{1}{2}, \cos 30^\circ = \frac{\sqrt{3}}{2}, \tan 30^\circ = \frac{1}{\sqrt{3}}}$ .
For $\boldsymbol{60^\circ}$ :
$\displaystyle\boldsymbol{\sin 60^\circ = \frac{\sqrt{3}}{2}, \cos 60^\circ = \frac{1}{2}, \tan 60^\circ = \sqrt{3}}$ .

Applications of Trigonometric Ratios for Standard Angles

Practical Uses

Solving Geometry Problems Involving Known Angles
- Identifying Unknown Sides:
  Trigonometric ratios for standard angles help determine unknown side lengths of triangles when at least one side and an angle are known.
  - Example: In a $\boldsymbol{30^\circ - 60^\circ - 90^\circ}$ triangle, the sides are in the ratio $\boldsymbol{1 : \sqrt{3} : 2}$ . Using this, you can quickly calculate side lengths.
- Verifying Shapes:
  Standard angles are used to analyze and verify geometric shapes like squares, equilateral triangles, and isosceles triangles.
Simplifying Calculations in Height and Distance Problems
- Height of an Object:
  Standard angles are used to find the height of an object using the angle of elevation and a known horizontal distance.
  - Example:
    If the angle of elevation to the top of a building is $\boldsymbol{30^\circ}$ and the distance from the base is $\boldsymbol{50 , \text{meters}}$ , then:
    $\displaystyle\boldsymbol{\tan 30^\circ = \frac{\text{Height}}{\text{Distance}}}$
    $\displaystyle\boldsymbol{\frac{1}{\sqrt{3}} = \frac{\text{Height}}{50}}$
    $\displaystyle\boldsymbol{\text{Height} = \frac{50}{\sqrt{3}} \approx 28.87 , \text{meters}}$ .
- Distance Between Two Points:
  By using the angle of depression and a known height, the horizontal distance can be calculated.
Applications in Physics
- Wave Motion:
  Trigonometric functions, including standard angles, describe the oscillatory behavior of sound and light waves.
  Example: A wave’s displacement can be expressed as $\boldsymbol{y = A \sin \omega t}$ , where $\boldsymbol{\sin \theta}$ is evaluated at standard angles.
- Projectile Motion:
  The range and height of projectiles depend on trigonometric functions of the launch angle:
  - Range: $\displaystyle\boldsymbol{R = \frac{v^2 \sin 2\theta}{g}}$
  - Maximum Height: $\displaystyle\boldsymbol{H = \frac{v^2 \sin^2 \theta}{2g}}$
    Here, standard angles like $\boldsymbol{45^\circ}$ are used for maximizing range.
- Resolving Forces:
  In mechanics, forces are often broken down into components along the x and y axes using $\boldsymbol{\cos \theta}$ and $\boldsymbol{\sin \theta}$ .

Tips for Memorization

Use Patterns for $\boldsymbol{\sin \theta}$ and $\boldsymbol{\cos \theta}$

The trigonometric values of $\boldsymbol{\sin \theta}$ and $\boldsymbol{\cos \theta}$ for the standard angles ( $\boldsymbol{0^\circ}$ , $\boldsymbol{30^\circ}$ , $\boldsymbol{45^\circ}$ , $\boldsymbol{60^\circ}$ , $\boldsymbol{90^\circ}$ ) follow predictable patterns that can be memorized easily:

For $\boldsymbol{\sin \theta}$ :
The values increase from $\boldsymbol{0}$ to $\boldsymbol{1}$ in a symmetrical progression:
$\displaystyle\boldsymbol{\sin \theta = 0, \frac{1}{2}, \frac{1}{\sqrt{2}}, \frac{\sqrt{3}}{2}, 1}$
For $\boldsymbol{\cos \theta}$ :
The values decrease from $\boldsymbol{1}$ to $\boldsymbol{0}$ , mirroring $\boldsymbol{\sin \theta}$ :
$\displaystyle\boldsymbol{\cos \theta = 1, \frac{\sqrt{3}}{2}, \frac{1}{\sqrt{2}}, \frac{1}{2}, 0}$

Derive $\boldsymbol{\tan \theta}$ from $\displaystyle\boldsymbol{\frac{\sin \theta}{\cos \theta}}$

To find $\boldsymbol{\tan \theta}$ for any standard angle: $\displaystyle\boldsymbol{\tan \theta = \frac{\sin \theta}{\cos \theta}}$
Example:
- For $\displaystyle\boldsymbol{\theta = 30^\circ}$ : $\displaystyle\boldsymbol{\tan 30^\circ = \frac{\sin 30^\circ}{\cos 30^\circ} = \frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}} = \frac{1}{\sqrt{3}}}$
- For $\displaystyle\boldsymbol{\theta = 45^\circ}$ : $\displaystyle\boldsymbol{\tan 45^\circ = \frac{\sin 45^\circ}{\cos 45^\circ} = \frac{\frac{1}{\sqrt{2}}}{\frac{1}{\sqrt{2}}} = 1}$

Use Mnemonics

To memorize trigonometric values:

For $\boldsymbol{\sin \theta}$ :
Think of the pattern “0, 1/2, 1/√2, √3/2, 1.”
For $\boldsymbol{\cos \theta}$ :
Reverse the $\boldsymbol{\sin \theta}$ pattern: “1, √3/2, 1/√2, 1/2, 0.”

Practice Reciprocals

$\displaystyle\boldsymbol{\csc \theta = \frac{1}{\sin \theta}}$
$\displaystyle\boldsymbol{\sec \theta = \frac{1}{\cos \theta}}$
$\displaystyle\boldsymbol{\cot \theta = \frac{1}{\tan \theta}}$

Example:

$\displaystyle\boldsymbol{\csc 30^\circ = \frac{1}{\sin 30^\circ} = 2}$
$\displaystyle\boldsymbol{\sec 45^\circ = \frac{1}{\cos 45^\circ} = \sqrt{2}}$

Trigonometric Ratios of Some Specific Angles

Overview of Trigonometric Ratios for Specific Angles

Why These Angles Are Considered Standard

Trigonometric Ratios for Standard Angles

Key Angles

Table of Trigonometric Ratios

Explanation of Table

Derivation of Ratios for Specific Angles

For

For and

Summary of Ratios

Applications of Trigonometric Ratios for Standard Angles

Practical Uses

Tips for Memorization

Use Mnemonics

Practice Reciprocals

Related Topics

Related Posts

Table of Contents

Join Deeksha Vedantu

> PU + Competitive Exam CoachingPreferred Choice For Toppers25+ Years of Academic Excellence70k+ Success Stories

Related Pages

Latest Posts

Top Links

Top Resources

Top Links

Contact Us

Head Office

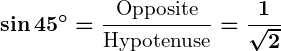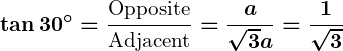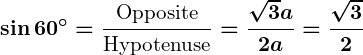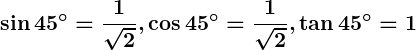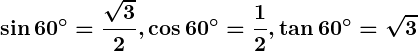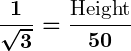
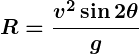
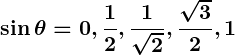
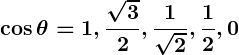
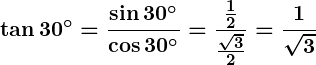
Get Social

For $\boldsymbol{45^\circ}$

For $\boldsymbol{30^\circ}$ and $\boldsymbol{60^\circ}$