8.5 Relationship Between A.M. and G.M. – Class 11 Mathematics

Introduction

In mathematics, means are ways of finding representative values of two or more numbers. Among the various types of means, the Arithmetic Mean (A.M.) and the Geometric Mean (G.M.) are the most widely studied in algebra and inequalities.

• Arithmetic Mean (A.M.) represents the average value.
• Geometric Mean (G.M.) represents the central tendency in multiplicative situations.

An extremely important inequality connects them:

A.M. ≥ G.M. for any two non-negative real numbers.

This inequality not only serves as a foundation for many mathematical results but also appears in competitive exams (JEE, KCET, COMEDK, Olympiads) and higher studies in mathematics, statistics, and economics.

Arithmetic Mean (A.M.)

If two positive numbers a and b are given, the Arithmetic Mean (A.M.) is:

A.M. = (a + b) / 2

It is simply the average of the two numbers.

Example:
For a = 4, b = 9:
A.M. = (4 + 9)/2 = 13/2 = 6.5

Geometric Mean (G.M.)

If two positive numbers a and b are given, the Geometric Mean (G.M.) is:

G.M. = √(ab)

It represents the mean proportional between a and b.

Example:
For a = 4, b = 9:
G.M. = √(4 × 9) = √36 = 6

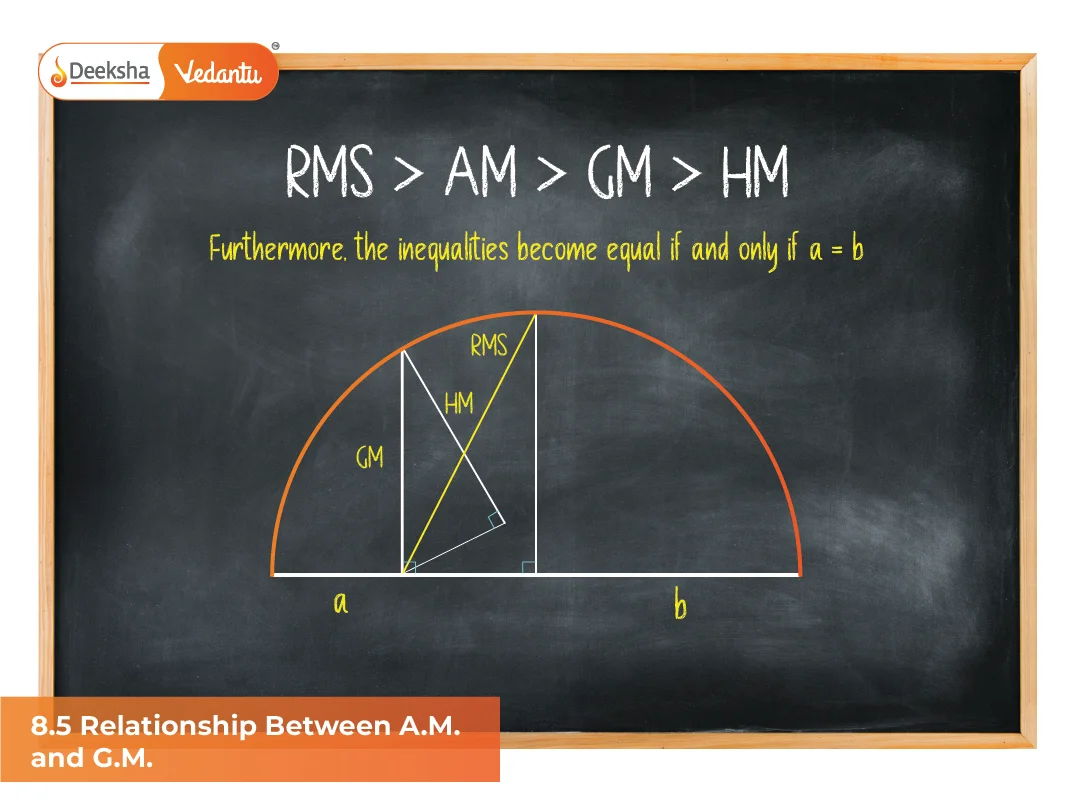
The A.M.–G.M. Inequality

For two positive real numbers a and b:

(a + b)/2 ≥ √(ab)

Equality holds if and only if a = b.

This is called the Arithmetic Mean–Geometric Mean Inequality (or A.M.–G.M. Inequality).

Proof of A.M.–G.M. Inequality

Method 1: Algebraic Proof

Let a, b ≥ 0.
We know: (a – b)² ≥ 0
⇒ a² – 2ab + b² ≥ 0
⇒ a² + b² ≥ 2ab
Divide both sides by 2:
(a² + b²)/2 ≥ ab
Take square root:
√[(a² + b²)/2] ≥ √ab
But note that (a + b)² ≥ a² + b².
Thus, (a + b)/2 ≥ √ab

Hence proved.

Method 2: Using Cauchy-Schwarz Inequality

For any real numbers:
(a² + b²)(1² + 1²) ≥ (a × 1 + b × 1)²
⇒ 2(a² + b²) ≥ (a + b)²
⇒ (a + b)² ≤ 2(a² + b²)
⇒ (a + b)/2 ≥ √(ab)

Method 3: Graphical Interpretation

Consider the parabola y = x².
By Jensen’s inequality for convex functions, the mean of values is greater than or equal to the function of the mean.

This proves A.M. ≥ G.M.

Extension to n Numbers

For n positive numbers a₁, a₂, a₃, …, aₙ:

Arithmetic Mean (A.M.) = (a₁ + a₂ + … + aₙ)/n
Geometric Mean (G.M.) = ⁿ√(a₁a₂a₃…aₙ)

Inequality:
A.M. ≥ G.M.

Equality holds if all a₁ = a₂ = … = aₙ.

Applications of A.M.–G.M. Inequality

1. Optimization Problems:
   • Maximizing or minimizing expressions.
   • Example: Find the minimum value of x + 1/x.
2. Inequality Proofs:
   • Used to show bounds in algebraic expressions.
3. JEE Advanced and Olympiads:
   • Frequently appears in inequality-based problems.
4. Economics and Finance:
   • G.M. is used for average growth rates (compounding), while A.M. is used for simple averages.

Solved Examples

Example 1:

Verify A.M. ≥ G.M. for a = 5, b = 20.

A.M. = (5 + 20)/2 = 12.5
G.M. = √(5 × 20) = √100 = 10
Thus A.M. (12.5) ≥ G.M. (10)

Example 2:

Find the minimum value of x + 9/x for x > 0.

Let a = x, b = 9/x
By A.M.–G.M. inequality:
(x + 9/x)/2 ≥ √(x × 9/x) = √9 = 3
⇒ x + 9/x ≥ 6

So the minimum value is 6, when x = 3.

Example 3:

If a and b are two positive numbers with sum 10, show that their product is maximum when a = b.

We know: A.M. ≥ G.M.
(a + b)/2 ≥ √(ab)
Given a + b = 10 ⇒ A.M. = 5
So √(ab) ≤ 5 ⇒ ab ≤ 25

The product ab is maximum at 25, when a = b = 5.

Example 4:

Prove that for any positive real numbers x, y:
(x + y)/2 ≥ √(xy).

This is the direct A.M.–G.M. inequality, already proven.

Example 5:

Show that A.M. of 3, 12, and 27 is greater than their G.M.

A.M. = (3 + 12 + 27)/3 = 42/3 = 14
G.M. = ³√(3 × 12 × 27) = ³√972 ≈ 9.94
Clearly, A.M. (14) > G.M. (9.94)

Advanced Problems for JEE & KCET

1. Find the minimum value of 2x + 8/x, for x > 0.
2. If a + b + c = 12, show that abc ≤ 64.
3. Using A.M.–G.M., prove that (1 + x + x²)/3 ≥ √(x³), for x > 0.
4. If the arithmetic mean of two numbers is 10 and their geometric mean is 8, find the numbers.

Common Mistakes

1. Applying A.M.–G.M. when numbers are negative.
   (It is valid only for non-negative numbers).
2. Forgetting that equality holds only when all numbers are equal.
3. Misapplying in optimization problems without checking domain constraints.

Exam Applications

• CBSE Boards: Questions of 4–6 marks to prove inequalities.
• JEE Main: Direct problems on optimization (2–4 marks).
• KCET/COMEDK: Quick calculation-based MCQs.
• JEE Advanced: Complex inequality-based applications with multiple variables.

Marks Allotment

• CBSE Board: 4–6 marks
• JEE Main: 1 question (2–4 marks)
• KCET/COMEDK: 1 question (2–3 marks)
• JEE Advanced: 4–6 marks indirectly (as part of inequalities or optimization problems)

FAQs

Q1. What is the basic inequality between A.M. and G.M.?
For non-negative numbers, A.M. ≥ G.M.

Q2. When does equality hold?
When all numbers are equal.

Q3. Why is A.M.–G.M. important in exams?
It is used in optimization, inequality problems, and proofs.

Q4. Can A.M. ever be less than G.M.?
No, for positive numbers it is always greater or equal.

Q5. Is A.M.–G.M. used in real life?
Yes, in finance (average returns), growth models, and scientific averages.