Derivatives form the cornerstone of calculus and are a powerful mathematical tool used to study change. In simple terms, a derivative measures how a function changes as its input changes. For JEE aspirants, this chapter not only introduces the fundamental concept of differentiation but also provides the techniques used in physics, engineering, and economics to analyze motion, growth, and optimization.
Understanding derivatives is essential for tackling higher-level topics such as continuity, differentiability, maxima-minima, and integral calculus. The chapter also includes important differentiation formulas, practical applications, and problem-solving strategies that appear in both JEE Main and JEE Advanced.
Marks Weightage in JEE
In JEE, derivatives hold substantial weightage about 8 –10 marks on average across both Main and Advanced papers. Questions typically involve direct computation, application of rules, or combined problems featuring continuity and differentiability. Students can expect one or two questions directly based on this concept, often requiring fast and accurate computation.
Introduction to Derivatives
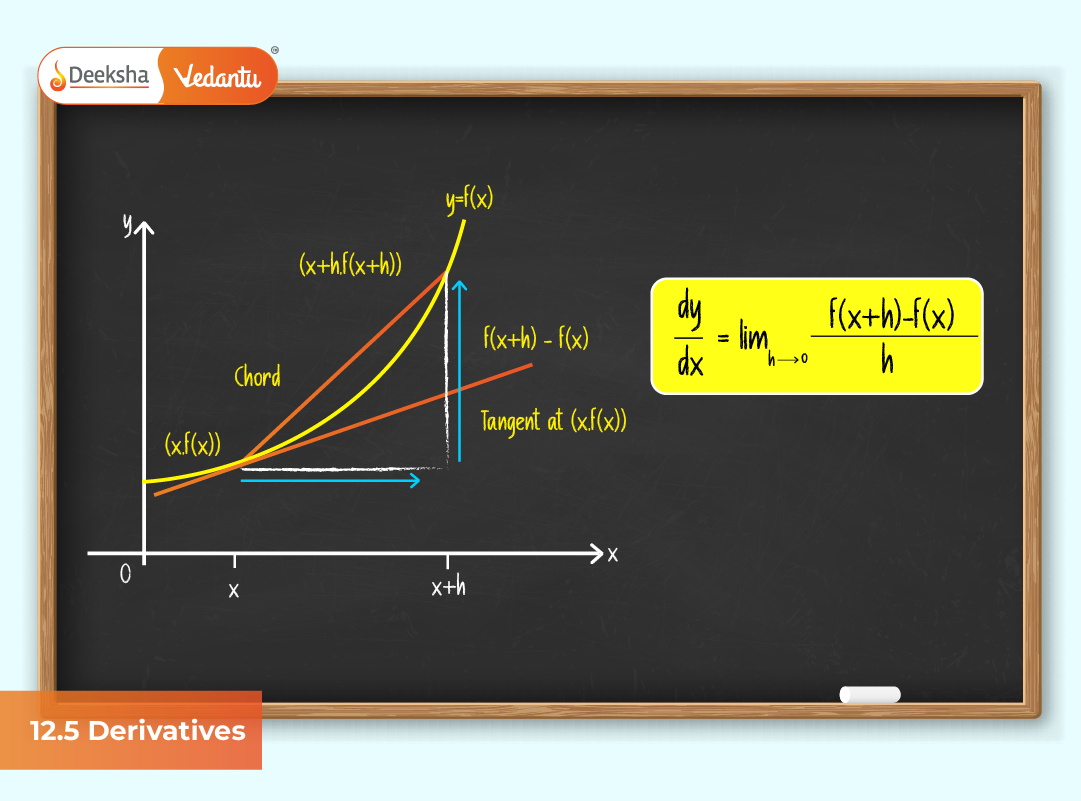
A derivative represents the rate at which one quantity changes with respect to another. Mathematically, if y = f(x), then the derivative of f(x) with respect to x is given as:
f'(x) = lim(h→0) [(f(x + h) − f(x)) / h]
This formula expresses the idea of the slope of the tangent line to the curve y = f(x) at a point x. The concept of limits, discussed in the previous sections, forms the foundation for understanding derivatives.
Example
Let f(x) = x². Then:
f'(x) = lim(h→0) [(x + h)² − x²] / h
= lim(h→0) [(x² + 2xh + h² − x²) / h]
= lim(h→0) [2x + h] = 2x.
Thus, the derivative of x² is 2x.
This approach, known as differentiation from first principles, gives an intuitive understanding of how derivatives work.
Algebra of Derivatives of Functions
Once the concept of derivatives is understood, several rules make the process faster and more efficient. These algebraic rules simplify the differentiation of complex functions.
(a) Constant Rule
If f(x) = c, where c is a constant, then f'(x) = 0.
(b) Power Rule
If f(x) = xⁿ, then f'(x) = n xⁿ⁻¹.
(c) Sum Rule
If f(x) = g(x) + h(x), then f'(x) = g'(x) + h'(x).
(d) Difference Rule
If f(x) = g(x) − h(x), then f'(x) = g'(x) − h'(x).
(e) Product Rule
If f(x) = g(x) × h(x), then f'(x) = g'(x)h(x) + g(x)h'(x).
(f) Quotient Rule
If f(x) = g(x) / h(x), then f'(x) = [g'(x)h(x) − g(x)h'(x)] / [h(x)]².
Example
Let f(x) = (x² + 3x)(x³ + 2).
Using product rule:
f'(x) = (2x + 3)(x³ + 2) + (x² + 3x)(3x²)
= 2x⁴ + 3x³ + 4x + 6 + 3x⁴ + 9x³
= 5x⁴ + 12x³ + 4x + 6.
These algebraic formulas significantly reduce the time taken in solving JEE questions.
Derivative of Polynomials and Trigonometric Functions
This section introduces how to differentiate standard polynomial and trigonometric functions directly using known rules.
Derivatives of Basic Functions
- If f(x) = xⁿ, then f'(x) = n xⁿ⁻¹.
- If f(x) = sin x, then f'(x) = cos x.
- If f(x) = cos x, then f'(x) = −sin x.
- If f(x) = tan x, then f'(x) = sec² x.
- If f(x) = cot x, then f'(x) = −csc² x.
- If f(x) = sec x, then f'(x) = sec x tan x.
- If f(x) = csc x, then f'(x) = −csc x cot x.
Example 1
f(x) = 3x³ + 5x² + 7x + 9.
Then f'(x) = 9x² + 10x + 7.
Example 2
f(x) = sin x + cos x.
Then f'(x) = cos x − sin x.
Example 3
f(x) = x² sin x.
Using product rule:
f'(x) = 2x sin x + x² cos x.
Example 4
f(x) = (sin x) / (cos x).
Using quotient rule:
f'(x) = [(cos x)(cos x) − (sin x)(−sin x)] / (cos x)²
= (cos² x + sin² x) / (cos x)² = sec² x.
Example 5
Find d/dx (tan³ x).
Using chain rule:
Let y = (tan x)³ = u³, where u = tan x.
Then dy/dx = 3u² (du/dx) = 3 tan² x × sec² x.
Chain Rule
When a function is composed of two or more functions, use the chain rule to find the derivative.
If y = f(g(x)), then dy/dx = f'(g(x)) × g'(x).
Example
Let y = sin(3x²).
Then dy/dx = cos(3x²) × 6x = 6x cos(3x²).
This rule is essential in JEE problems involving nested functions or trigonometric compositions.
Geometrical Meaning of Derivatives
The derivative of a function at a point represents the slope of the tangent to the curve at that point. If f'(x) is positive, the curve rises; if it’s negative, the curve falls. This interpretation forms the foundation for studying increasing and decreasing functions, maxima and minima, and concavity.
Example
For y = x², the slope at x = 1 is given by f'(1) = 2 × 1 = 2. Thus, the tangent at (1, 1) has slope 2.
Applications of Derivatives in JEE
Derivatives are applied in numerous ways:
- Finding the slope of a curve
- Determining maxima and minima of functions
- Solving rate of change problems
- Calculating motion (velocity and acceleration)
- Understanding tangents and normals
Example (Maxima-Minima)
Let f(x) = x³ − 6x² + 9x + 2.
Then f'(x) = 3x² − 12x + 9 = 3(x² − 4x + 3) = 3(x − 1)(x − 3).
At x = 1 and x = 3, the derivative changes sign, indicating extrema.
f”(x) = 6x − 12.
At x = 1, f”(x) = −6 (maximum), and at x = 3, f”(x) = 6 (minimum).
Hence, the curve has a maximum at (1, 6) and a minimum at (3, 2).
Important JEE-Based Examples
Problem 1
Find d/dx (sin x + tan x + x²).
Solution:
Derivative = cos x + sec² x + 2x.
Problem 2
Find d/dx [(x² + 1)(x³ − 2x)].
Derivative = (2x)(x³ − 2x) + (x² + 1)(3x² − 2).
Problem 3
If y = sin³ x + cos³ x, find dy/dx.
dy/dx = 3 sin² x cos x − 3 cos² x sin x = 3 sin x cos x (sin x − cos x).
Problem 4
If y = x tan x, find dy/dx.
Using product rule: dy/dx = tan x + x sec² x.
Problem 5
If y = (sin x) / x, find dy/dx.
Using quotient rule: dy/dx = [x cos x − sin x] / x².
Common Mistakes to Avoid
- Ignoring the chain rule when functions are nested.
- Forgetting to square the denominator in quotient rule.
- Differentiating constants incorrectly.
- Mixing radians and degrees in trigonometric derivatives.
- Skipping simplification after applying rules.
Tips for JEE Preparation
- Practice derivatives of all trigonometric, exponential, and logarithmic functions.
- Focus on chain rule and composite functions.
- Revise standard formulas weekly.
- Solve mixed-rule problems to improve speed.
- Attempt previous JEE papers to understand problem patterns.
FAQs
Q1: What is the derivative of xⁿ?
The derivative of xⁿ is n xⁿ⁻¹.
Q2: What is the derivative of sin x and cos x?
For sin x, it is cos x; for cos x, it is −sin x.
Q3: What is the geometrical meaning of derivatives?
It represents the slope of the tangent to the curve at a given point.
Q4: What rule is used for differentiation of composite functions?
The chain rule.
Q5: How important is this topic for JEE?
Extremely important. It serves as the base for continuity, maxima-minima, and integration problems.
Conclusion
The topic of derivatives builds the core understanding of change and motion in calculus. For JEE, mastering differentiation techniques is essential for tackling advanced questions in both mathematics and physics. Regular practice, clarity in formulas, and consistent revision will ensure high accuracy and speed in problem-solving.






Get Social