1.4 Uncertainty in Measurement – Class 11 Chemistry

In chemistry, accuracy and precision are essential for quantitative science. Every experiment relies on accurate measurements and a clear understanding of how uncertainty affects the results. The concept of uncertainty, significant figures, and dimensional analysis is central to developing problem-solving skills required for JEE and NEET. Understanding these aspects allows you to minimize errors and express results correctly.

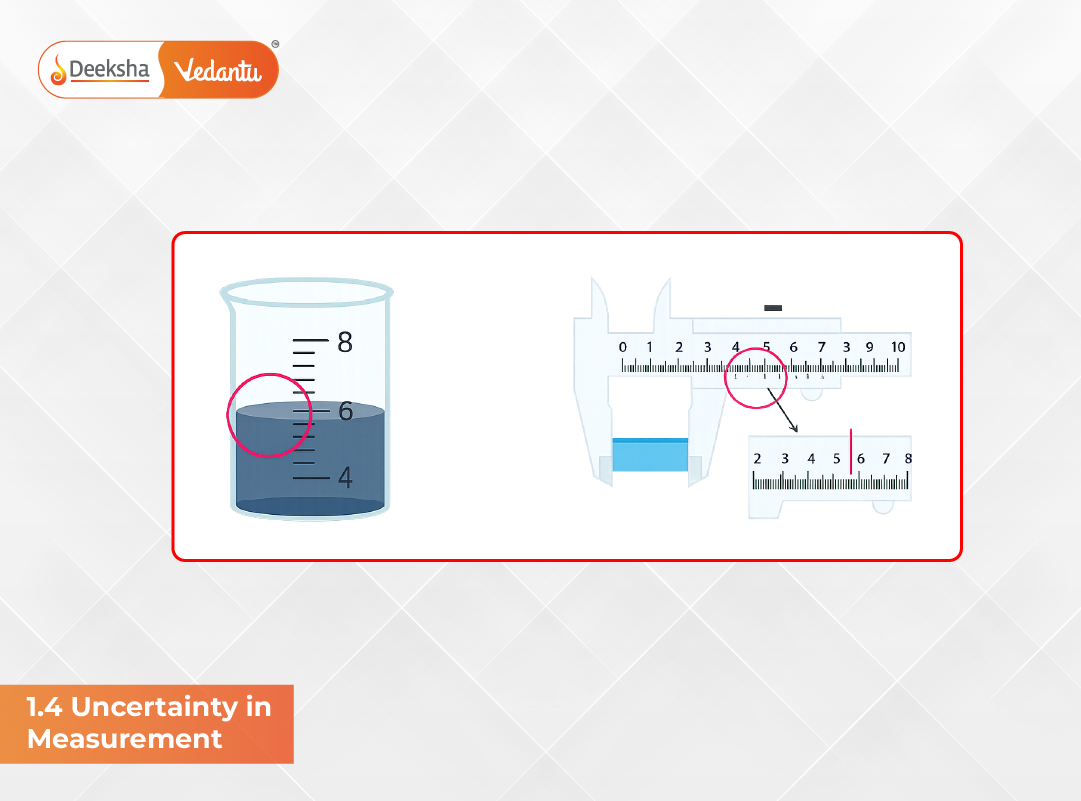
Uncertainty arises because no measurement is perfectly exact. The tools we use have limitations, and the experimenter’s judgment can introduce variation. Thus, every measurement must be represented with the degree of confidence it carries.

Scientific Notation

Scientific notation expresses large or small numbers in a compact, standardized form. This representation simplifies calculation and ensures precision when working with physical quantities.

A number in scientific notation is written as N × 10ⁿ, where 1 ≤ N < 10 and n is an integer.

Why It’s Important:

In chemistry and physics, constants like Avogadro’s number or Planck’s constant are extremely large or small. Expressing them in scientific notation prevents transcription errors and simplifies computation.

Example:

• 602200000000000000000000 (Avogadro’s number) = 6.022 × 10²³.
• 0.000000000000001 (atomic radius magnitude) = 1 × 10⁻¹⁵.

Rules:

1. Moving the decimal point to the left increases the exponent.
2. Moving the decimal to the right decreases the exponent.
3. Use only one non-zero digit before the decimal.

JEE Application Example:

Express 0.000456 in scientific notation.

• Decimal moved 4 places right → 4.56 × 10⁻⁴.

Explanation: Such conversions are often tested in unit and measurement-based JEE questions. Practicing these boosts calculation accuracy.

Advanced Example:

Calculate (6.022 × 10²³ × 1.66 × 10⁻²⁴).
= (6.022 × 1.66) × 10²³⁻²⁴ = 9.999 × 10⁻¹ ≈ 1.
This example demonstrates how exponents are added/subtracted efficiently.

Significant Figures

Significant figures indicate the precision of a measured quantity. They include all known digits plus the first uncertain digit.

Detailed Rules:

1. All non-zero digits are significant (e.g., 456 → 3 significant figures).
2. Zeros between non-zero digits are significant (e.g., 1002 → 4 significant figures).
3. Leading zeros before a non-zero digit are not significant (e.g., 0.0023 → 2 significant figures).
4. Trailing zeros after a decimal point are significant (e.g., 2.300 → 4 significant figures).
5. Trailing zeros without a decimal are not significant (e.g., 200 → 1 significant figure, but 200. → 3 significant figures).

Significant Figures in Calculations:

• Addition/Subtraction: Limit the decimal places to the least precise measurement.
• Multiplication/Division: Limit the result to the least number of significant figures.

Examples:

1. (2.5 × 3.42) = 8.55 → 8.6 (2 significant figures)
2. (5.00 + 1.245) = 6.25 (2 decimal places)

Importance in JEE:

These rules frequently appear in questions involving error propagation and data analysis. In such problems, an incorrect count of significant figures can change the entire solution.

Real-World Example:

In spectroscopy, measurement readings often involve uncertainties like 1.234 ± 0.002. Here, the result must be reported as 1.23 to maintain significance integrity.

Dimensional Analysis

Dimensional analysis provides a way to check equations, derive new formulas, and ensure unit consistency. It represents physical quantities in terms of basic dimensions — M (mass), L (length), T (time).

Common Dimensional Formulas:

• Velocity = [M⁰L¹T⁻¹]
• Acceleration = [M⁰L¹T⁻²]
• Force = [M¹L¹T⁻²]
• Pressure = [M¹L⁻¹T⁻²]
• Energy = [M¹L²T⁻²]

Applications:

1. Checking Equation Validity: 
   • Verify if equations like s = ut + ½at² are dimensionally correct.
   • LHS: [L]; RHS: [L¹] + [L¹] = [L]; ✅ Correct.
2. Deriving Relations:
   • Example: The time period T of a pendulum depends on length (l) and gravity (g).
   • Assume T = k lˣ gʸ.
   • Dimensional equation: [T¹] = [Lˣ] [L¹T⁻²]ʸ = [L]ˣ⁺ʸ[T]⁻²ʸ.
   • Equating exponents: 1 = -2y, 0 = x + y → x = ½, y = -½.
   • Hence, T = k(l/g)¹ᐟ².
3. Unit Conversion:
   • Convert 5 m/s to km/hr.
   • 5 × (3600/1000) = 18 km/hr.
4. Finding Dimensionless Quantities:
   • Reynolds number, coefficient of friction, and Poisson’s ratio have no dimension.

Advanced JEE Example:

A student derived v = √(2gh). Check dimensional correctness.

• LHS: [M⁰L¹T⁻¹]; RHS: (L¹T⁻²)¹ᐟ² = [L¹T⁻¹]. ✅ Correct. 

JEE Focused Insights

• Weightage: Typically 2–3 marks in JEE Main; 3–4 marks in JEE Advanced.
• Frequent Topics:
  • Dimensional equations of physical laws.
  • Conversion between CGS and SI systems.
  • Propagation of errors with significant figures.
  • Deriving new physical relationships.

Tips for JEE Aspirants:

• Memorize dimensional formulas for common physical constants.
• Practice dimensional checks for derived formulas.
• While using calculators, retain the correct number of significant digits.
• When in doubt, express results in scientific notation.

Sample JEE Exercise:

1. Express the speed of light (3.0 × 10⁸ m/s) in km/hr.
   • 3 × 10⁸ × (3600/1000) = 1.08 × 10⁹ km/hr.
2. Check if E = ½mv² is dimensionally correct.
   • [M¹L²T⁻²] ✅.

FAQs

Q1. What is the difference between precision and accuracy?

Precision shows consistency among repeated measurements, while accuracy shows how close a value is to the true standard or accepted value.

Q2. Why are significant figures important in chemical data?

They indicate the precision of a measurement, ensuring that reported results are neither over- nor under-estimated in their accuracy.

Q3. What is the dimensional formula of energy and power?

Energy = [M¹L²T⁻²]; Power = [M¹L²T⁻³].

Q4. How does scientific notation help in JEE problem-solving?

It streamlines lengthy numerical operations, especially those involving constants with large or small magnitudes.

Q5. Can dimensional analysis detect calculation errors?

Only dimensional errors — it cannot catch arithmetic or numerical coefficient mistakes.

Q6. How many significant figures should be retained in final JEE answers?

Generally, retain 2–3 significant figures unless specified in the question.

Q7. What is the base SI unit system used in chemistry?

The SI system (Système International) uses seven base units including meter (m), kilogram (kg), and second (s).

Conclusion

Uncertainty in measurement, significant figures, and dimensional analysis form the bedrock of accurate chemical and physical calculations. For JEE aspirants, these principles ensure logical consistency and error-free reasoning. Mastery of these tools enables efficient computation, reliable unit conversions, and validation of physical relationships. With practice, students can handle complex numerical problems confidently — a critical skill for securing top ranks in JEE.