Chapter 10: Conic Sections – Class 11 Mathematics

Introduction

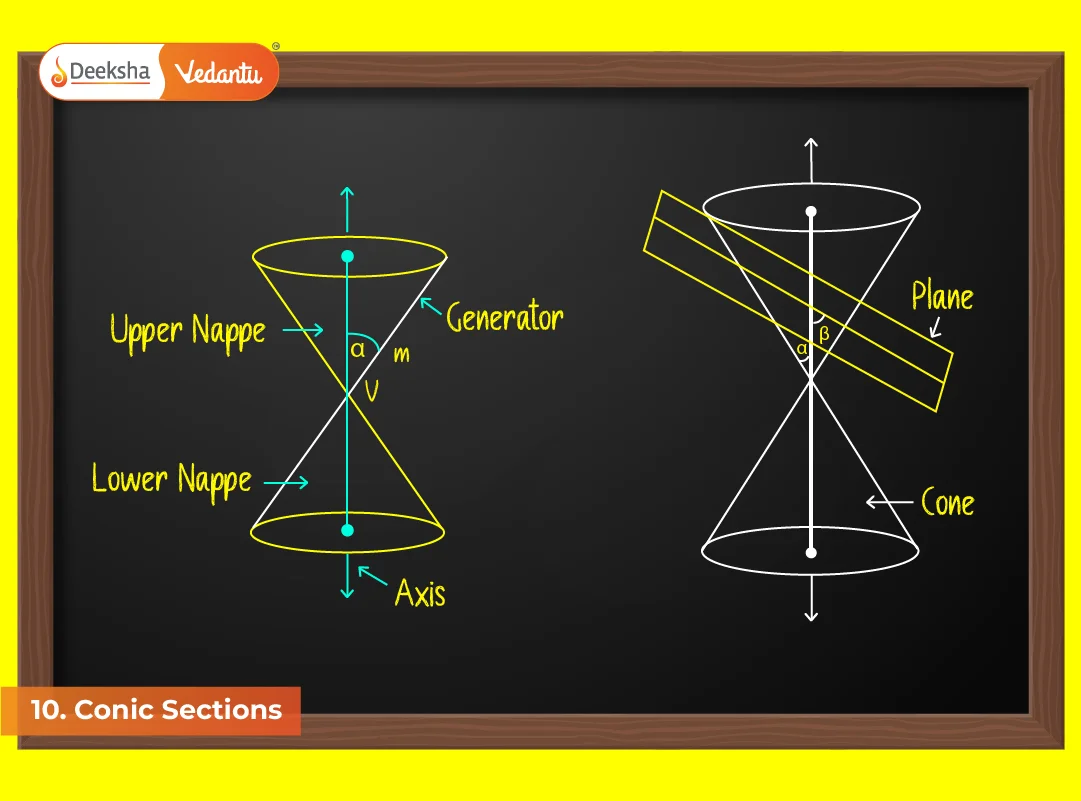
Conic Sections form one of the most important topics in Class 11 Mathematics. The word “conic” comes from the fact that these curves are obtained by the intersection of a plane with a double-napped right circular cone. The study of conic sections not only has historical importance (from Greek geometry to planetary orbits) but also forms the backbone of higher mathematics, physics, astronomy, and engineering.

In the JEE and KCET exams, conic sections are highly scoring because they involve direct formulas, geometric interpretations, and well-defined properties. From an NCERT perspective, the chapter is carefully structured to take students from the geometric definition to algebraic representation.

Why Study Conic Sections?

• Real-life applications: Orbits of planets (ellipse), satellite dishes (parabola), car headlights (parabolic reflectors), telescope mirrors (hyperbola).
• Mathematics applications: Understanding loci, quadratic equations in two variables, analytic geometry.
• Exams: A standard 2–3 questions appear from this chapter in JEE Main, KCET, and COMEDK each year.

Historical Context

The Greeks, particularly Apollonius of Perga, studied conic sections around 200 BCE. Later, Kepler used ellipses to describe planetary orbits. Newton showed that under the inverse-square law of gravitation, paths of celestial objects are conics. This makes conics not just mathematical curves but cosmic realities.

Classification of Conic Sections

Conic sections are classified into circle, ellipse, parabola, and hyperbola depending on the angle of intersection of a plane with a cone.

1. Circle – special ellipse with eccentricity e = 0.
2. Ellipse – set of all points where sum of distances from two fixed points (foci) is constant.
3. Parabola – set of all points equidistant from a fixed point (focus) and a fixed line (directrix).
4. Hyperbola – set of all points where difference of distances from two fixed points (foci) is constant.

Analytical Geometry and Conics

Conic sections are studied algebraically using Cartesian coordinates. By using coordinate geometry, equations of conics can be written in standard forms, and properties like eccentricity, focus, directrix, and latus rectum can be derived systematically.

Subtopics Covered in This Chapter

10.2 Sections of a Cone

• Basic idea of how conics are generated.
• Circle, ellipse, parabola, hyperbola derived from plane–cone intersections.
• Role of eccentricity (e) in classification:
  • e = 0 → circle
  • 0 < e < 1 → ellipse
  • e = 1 → parabola
  • e > 1 → hyperbola

10.3 Circle

• Definition: set of all points equidistant from a fixed point (centre).
• Equation: (x – h)² + (y – k)² = r².
• General form of equation of circle.
• Conditions for tangency and intersection.
• Solved examples with tangents, normals, and chords.

10.4 Parabola

• Definition: locus of a point equidistant from focus and directrix.
• Standard equation: y² = 4ax (axis along x-axis).
• Other forms depending on axis orientation.
• Terms: vertex, focus, directrix, axis, latus rectum.
• Applications in physics and optics.

10.5 Ellipse

• Definition: set of points where sum of distances from two foci is constant.
• Standard equation: (x²/a²) + (y²/b²) = 1.
• Major axis, minor axis, foci, eccentricity e = √(1 – b²/a²).
• Properties of ellipse and solved examples.

10.6 Hyperbola

• Definition: set of points where difference of distances from foci is constant.
• Standard equation: (x²/a²) – (y²/b²) = 1.
• Conjugate hyperbola, asymptotes.
• Eccentricity e > 1.
• Applications in astronomy and communication devices.

Marks Allotment (CBSE, JEE, KCET/COMEDK)

• CBSE Boards: 10–12 marks (long answer questions on standard equations and properties).
• JEE Main: 2–3 questions (approx. 8–12 marks). Mostly standard forms, eccentricity, tangent-normal conditions.
• KCET/COMEDK: 2–3 questions (each 2–3 marks). Focus on direct formulas and locus-based problems.
• JEE Advanced: Often involves conceptual questions combining conics with locus and transformations.

Common Applications in Competitive Exams

• Finding the equation of tangent to conic at a point.
• Equation of normal.
• Directrix-focus property based problems.
• Locus of points satisfying conic conditions.
• Family of conics passing through given points.

Practice Questions (Chapter-level)

1. Write equation of a circle with centre (2, –3) and radius 5. 
2. Find focus, directrix, and latus rectum length for parabola y² = 12x. 
3. Find eccentricity of ellipse x²/25 + y²/16 = 1. 
4. Find equation of tangent to ellipse x²/16 + y²/9 = 1 at point (2, √5). 
5. Find equation of hyperbola with transverse axis along x-axis, centre at origin, a = 5, b = 4. 
6. Find locus of point equidistant from (0, 3) and line y = –3. 
7. Write equations of conjugate hyperbola of (x²/9) – (y²/16) = 1. 
8. Prove that parabola y² = 4ax has focus (a, 0). 
9. Find condition for line y = mx + c to be tangent to circle x² + y² = r². 
10. Find eccentricity of hyperbola (x²/9) – (y²/16) = 1. 

FAQs

Q1. What is eccentricity in conics?
It measures how much a conic deviates from being circular.

Q2. Which conic has eccentricity = 1?
Parabola.

Q3. Which conic is most important for JEE?
All are important, but the ellipse and parabola have maximum weightage.

Q4. Why is hyperbola less common in board exams?
Because its applications are fewer in NCERT syllabus, but JEE still asks conceptual questions.

Q5. What is the best strategy to master conics?
Understand definitions geometrically, memorize standard equations, and practice tangent-normal derivations.

Conclusion

The study of Sections of a Cone lays the foundation for understanding all conic sections – circle, ellipse, parabola, and hyperbola. By varying the angle and position of the cutting plane, we derive different curves, each with unique properties and applications.

Through the concept of eccentricity (e), we unify these curves under a single definition:

• e = 0 → Circle
• 0 < e < 1 → Ellipse
• e = 1 → Parabola
• e > 1 → Hyperbola

This classification not only helps in understanding the geometric nature of conics but also prepares students for deeper algebraic analysis in upcoming sections. Whether in CBSE boards, JEE, KCET, or COMEDK, the ability to quickly identify and work with conic sections is a vital skill for problem-solving.