2.3 Developments Leading to the Bohr’s Model of Atom – Class 11 Chemistry

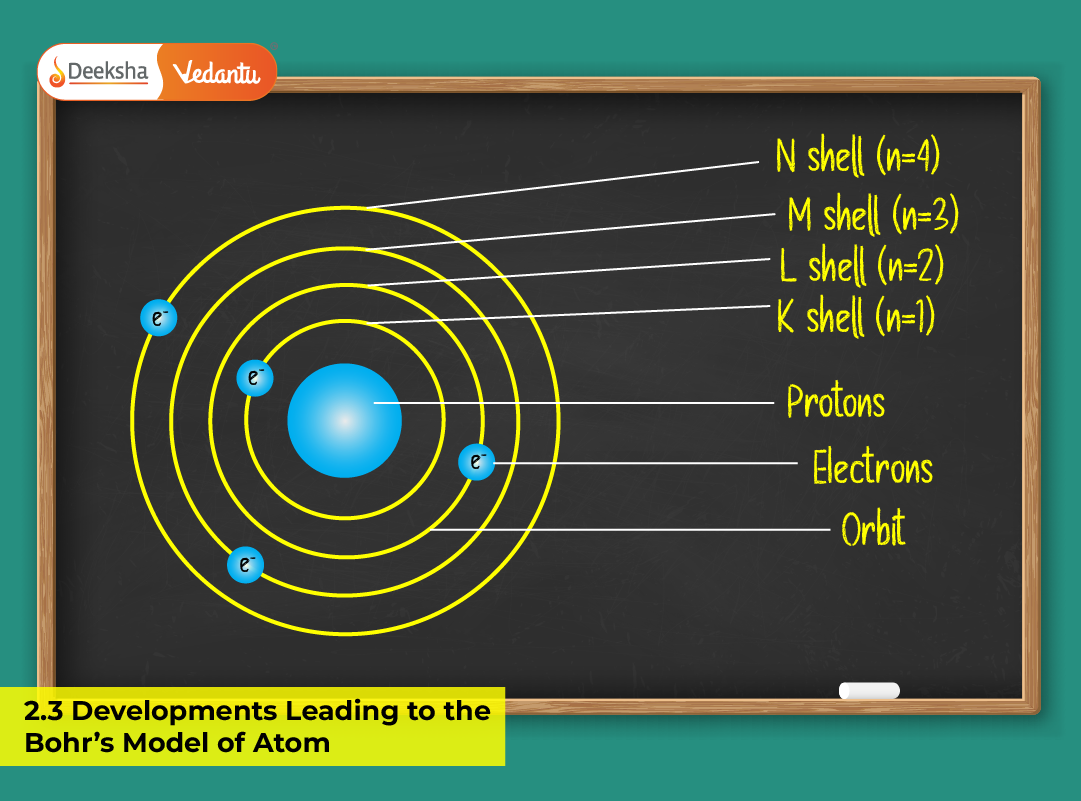
Introduction

Before Niels Bohr revolutionized atomic theory in 1913, science witnessed a period of intense discovery between 1880 and 1910. Physicists and chemists began uncovering clues about the fundamental behavior of energy and matter, realizing that classical Newtonian mechanics could not explain atomic and subatomic phenomena. The understanding of electromagnetic radiation, blackbody radiation, Planck’s quantum hypothesis, and Einstein’s photoelectric effect reshaped the foundation of atomic physics. These breakthroughs ultimately paved the way for the quantum model of the atom, influencing Bohr’s theory of quantized electron orbits.

Electromagnetic Radiation

Electromagnetic radiation is a form of energy emitted and absorbed by charged particles. It travels through space as oscillating electric and magnetic fields that are perpendicular to each other and to the direction of wave propagation. The electromagnetic spectrum covers a wide range of frequencies and wavelengths — from radio waves to gamma rays — all traveling at the speed of light (3 × 10⁸ m/s).

Key Characteristics

• Does not require a medium to propagate.
• Possesses both wave-like and particle-like nature.
• The relationship between wavelength (λ), frequency (ν), and speed of light (c) is:
  c = λν
• The energy of radiation increases as the frequency increases.

The electromagnetic spectrum is classified into regions such as radio, microwave, infrared, visible light, ultraviolet, X-rays, and gamma rays. Each region has unique applications—from wireless communication to medical imaging.

JEE & NEET Insight

Students must understand the inverse relationship between wavelength and frequency. Higher frequency means shorter wavelength and greater photon energy. This concept is widely tested in JEE and NEET problem-solving on energy transitions and spectral analysis.

Example Question (JEE Level)

Q: Calculate the wavelength of radiation with frequency 6 × 10¹⁴ Hz.
A: λ = c/ν = (3 × 10⁸) / (6 × 10¹⁴) = 5 × 10⁻⁷ m (or 500 nm — green visible light).

Example Question (Advanced Application)

Q: If light of frequency 7.5 × 10¹⁴ Hz passes from air into glass with refractive index 1.5, what happens to wavelength and frequency?
A: Frequency remains constant, wavelength decreases: λ₂ = λ₁/n = 500/1.5 = 333 nm.

Blackbody Radiation and Planck’s Quantum Theory

A blackbody is an idealized object that absorbs all incident radiation and emits energy uniformly in all directions. Classical physics predicted an infinite rise in intensity at short wavelengths (the ultraviolet catastrophe), which experimental results contradicted.

Planck’s Quantum Hypothesis

In 1900, Max Planck proposed that atoms emit or absorb energy in discrete packets called quanta, not continuously. The energy of each quantum is given by:
E = hν,
where h = 6.626 × 10⁻³⁴ J·s.

This idea marked the beginning of quantum theory, fundamentally challenging classical concepts.

Importance

• Introduced the concept of energy quantization.
• Explained the intensity distribution of blackbody radiation.
• Laid the groundwork for the concept of photons and quantum transitions.

Extended Discussion

Planck’s discovery also influenced chemical bonding and electronic behavior. The quantization of vibrational energy levels in molecules helped explain specific heat capacities and emission spectra.

Example Question

Q: Find the energy of a photon with wavelength 400 nm.
A: E = hc/λ = (6.626 × 10⁻³⁴ × 3 × 10⁸) / (400 × 10⁻⁹) = 4.97 × 10⁻¹⁹ J.

Example Question 4 (Conceptual)

Why was Planck’s hypothesis revolutionary?
Because it abandoned the idea of continuous energy transfer and introduced quantization, providing a solution to blackbody radiation anomalies.

Photoelectric Effect

Einstein, in 1905, explained that light consists of discrete particles or photons. When light of sufficient frequency strikes a metal surface, it ejects electrons. This experiment confirmed the particle nature of light.

Key Observations

• Below a certain threshold frequency, no electrons are emitted, regardless of light intensity.
• The kinetic energy of emitted electrons increases with the frequency of light, not intensity.
• The number of electrons emitted is proportional to intensity.

Einstein’s Equation

K.E. = hν – W
where W = work function (minimum energy needed to remove an electron).

Significance

This effect proved that energy transfer occurs in discrete quanta, validating Planck’s concept. It also showed that light’s behavior cannot be explained by wave theory alone.

Example Problem

Q: If the work function of potassium is 2.3 eV, find the threshold wavelength.
A: λ = hc/W = (6.626 × 10⁻³⁴ × 3 × 10⁸) / (2.3 × 1.6 × 10⁻¹⁹) ≈ 540 nm.

NEET Insight

This concept forms the basis for solar cells and photodiodes. Students must relate frequency, work function, and energy to predict electron emission.

Dual Nature of Electromagnetic Radiation

The dual nature of light unifies its wave and particle characteristics. Experiments like diffraction and interference demonstrate its wave behavior, while the photoelectric effect proves its particle nature.

Wave Behavior

• Responsible for phenomena such as interference, reflection, and refraction.
• Described mathematically by Maxwell’s electromagnetic equations.

Particle Behavior

• Explained by the existence of photons (quantized packets of energy).
• Supported by photoelectric and Compton scattering experiments.

Application to Bohr’s Model

Bohr incorporated quantum ideas by proposing that electrons revolve in discrete orbits and emit or absorb photons when transitioning between levels. The energy of the emitted or absorbed photon equals the energy difference between orbits:
E₂ – E₁ = hν.

Example JEE Question

Q: Why doesn’t increasing the intensity of low-frequency light cause photoemission?
A: Because each photon’s energy is below the threshold energy (E = hν < W). Increasing intensity adds more photons but not higher-energy ones.

Extended JEE & NEET Focus Points

• Derive E = hc/λ and connect it with Planck’s relation.
• Solve numerical questions on threshold frequency and energy transitions.
• Compare classical and quantum models of energy emission.
• Understand the difference between continuous and discrete energy distributions.
• Analyze real-world uses: solar panels, LEDs, X-ray production.

Advanced Practice Problems for JEE/NEET

1. Derivation: Prove that photon energy increases with frequency and calculate for λ = 250 nm.
2. Numerical: If light of 300 nm ejects electrons with kinetic energy 1.5 eV, calculate the work function.
3. Application: Discuss how quantization explains hydrogen spectral lines.
4. Reasoning: Why did classical wave theory fail to explain atomic stability?
5. Numerical: Determine energy of photons with ν = 8 × 10¹⁴ Hz.

FAQs

Q1. What is electromagnetic radiation?

It is a form of energy that travels through space as oscillating electric and magnetic fields, covering a range from radio waves to gamma rays.

Q2. What does Planck’s theory state?

It states that energy is emitted or absorbed in discrete units (quanta), each having energy proportional to its frequency.

Q3. How did the photoelectric effect support quantum mechanics?

It proved that light transfers energy in discrete packets (photons), not continuous waves, confirming the quantized nature of energy.

Q4. What is meant by the dual nature of light?

Light behaves as both a wave (in diffraction) and a particle (in photoelectric emission), unifying electromagnetic and quantum theories.

Q5. How did these discoveries lead to Bohr’s model?

They established that atomic energy levels are quantized, enabling Bohr to explain atomic stability and discrete spectral lines.

Conclusion

The discoveries that led to Bohr’s atomic model marked the transition from classical to quantum physics. Understanding electromagnetic radiation, Planck’s quantum theory, and Einstein’s photoelectric effect helped scientists realize that energy is quantized. These principles not only shaped Bohr’s model but also laid the groundwork for modern quantum mechanics. For JEE and NEET aspirants, mastering these topics enhances conceptual depth and problem-solving skills in topics like atomic structure, spectral transitions, and quantum energy calculations.