
Introduction
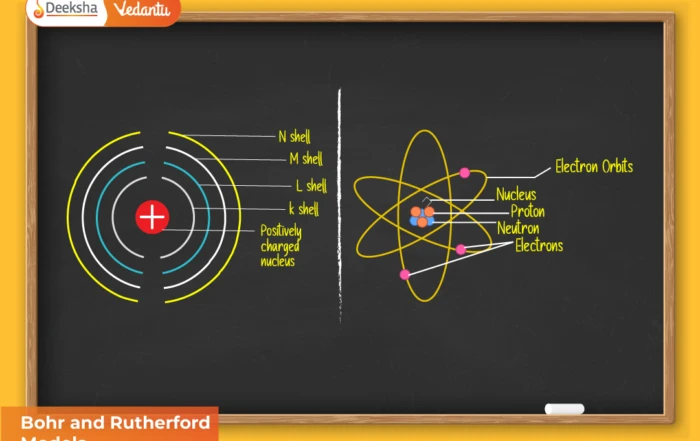
The Bohr Model of the Hydrogen Atom, introduced by Niels Bohr in 1913, revolutionized our understanding of atomic structure. Building upon Rutherford’s nuclear model and Planck’s quantum hypothesis, Bohr proposed that electrons revolve in quantized orbits, each with a specific energy level. This theory successfully explained the stability of atoms and the discrete line spectra of hydrogen, which classical physics could not justify. The Bohr model marked the beginning of the quantum era, bridging the gap between the deterministic world of Newtonian mechanics and the probabilistic nature of quantum theory.
Postulates of Bohr’s Model
Bohr proposed four fundamental postulates to explain the structure and behavior of electrons in an atom:
- Quantized Orbits: Electrons revolve around the nucleus only in specific circular orbits known as stationary states. These orbits have fixed energies and radii, ensuring stability and no energy radiation while revolving.
- Stationary Energy Levels: Each orbit corresponds to a distinct energy level, represented by a principal quantum number (n = 1, 2, 3,…). The electron’s energy remains constant as long as it stays within that orbit.
- Emission and Absorption of Energy: Electrons absorb or emit energy only when they transition between two permitted energy levels. The energy difference corresponds to the frequency of the emitted or absorbed radiation:
E₂ – E₁ = hν
where h is Planck’s constant and ν is the frequency of the photon. - Quantization of Angular Momentum: The angular momentum of an electron is quantized and given by:
mvr = n(h/2π)
Here, m is the mass of the electron, v is its velocity, r is the orbit radius, and n is the principal quantum number. This quantization prevents electrons from spiraling into the nucleus.
These postulates unified concepts of energy quantization, electromagnetic radiation, and atomic stability, creating a strong theoretical base for modern quantum mechanics.
Derivation of Energy Levels in the Hydrogen Atom
Bohr derived the formula for energy levels by combining electrostatic and centrifugal forces acting on the electron:
k e² / r² = mv² / r
Substituting the quantized angular momentum relation (mvr = nh/2π) gives the radius of the nth orbit:
rₙ = (ε₀ h² n²) / (π m e²)
The corresponding energy of the electron in the nth orbit is:
Eₙ = – (me⁴) / (8 ε₀² h² n²)
For hydrogen, this simplifies to:
Eₙ = -13.6 / n² eV
The negative sign indicates that the electron is bound to the nucleus. The smaller the value of n, the greater the binding energy, meaning the electron is closer to the nucleus and more stable.
Expanded JEE/NEET Sample Calculations
Example 1: Calculate the radius of the third orbit of hydrogen.
r₃ = 0.529 × n² Å = 0.529 × 9 = 4.76 Å.
Example 2: Determine the energy released when an electron transitions from n=3 to n=2.
E = 13.6(1/2² – 1/3²) = 1.89 eV.
Example 3: Find the velocity of an electron in the first orbit of hydrogen.
v₁ = e² / (2ε₀ h) = 2.18 × 10⁶ m/s.
Such calculations are crucial for understanding the atomic energy transitions tested in JEE and NEET physics sections.
Explanation of Hydrogen Line Spectrum
The Bohr model effectively explained hydrogen’s emission and absorption spectra. When an electron in a higher orbit transitions to a lower one, it emits energy as electromagnetic radiation. The wavelength or frequency of this radiation corresponds to the energy difference between two levels.
ν = R_H (1/n₁² – 1/n₂²)
Here, R_H = 1.097 × 10⁷ m⁻¹ (Rydberg constant). Each transition corresponds to a spectral line, forming the hydrogen spectral series.
Hydrogen Spectral Series Table
| Series | Transition (n₂ → n₁) | Spectral Region | Typical Example |
| Lyman | n₂ → 1 | Ultraviolet | 121.6 nm |
| Balmer | n₂ → 2 | Visible | 656.3 nm (red) |
| Paschen | n₂ → 3 | Infrared | 1875 nm |
| Brackett | n₂ → 4 | Infrared | 4050 nm |
| Pfund | n₂ → 5 | Infrared | 7460 nm |
JEE-Level Application Example
Q: Calculate the wavelength of the line in the Balmer series corresponding to n₂ = 4 → n₁ = 2.
A: Using ν = R_H (1/2² – 1/4²), λ = 486 nm (blue-green line). This is one of the most prominent Balmer lines.
Limitations of Bohr’s Model
While revolutionary, Bohr’s model had its constraints:
- Could not explain spectra of multi-electron atoms or fine structures.
- Failed to account for the Zeeman effect (magnetic field splitting) and Stark effect (electric field splitting).
- Ignored electron wave nature and Heisenberg’s uncertainty principle.
- Could not explain transition probabilities or spectral intensities.
Despite these drawbacks, the model remains a fundamental stepping stone to quantum mechanics and atomic theory.
JEE & NEET Conceptual Insights
- Master derivation of Eₙ = -13.6/n² and the concept of quantized angular momentum.
- Solve numerical problems on wavelength, transition energy, and ionization potential.
- Understand spectral series relationships and their practical implications.
- Apply the concept of hydrogen-like ions (He⁺, Li²⁺) using Z² dependency.
- Recognize how the Bohr model laid the groundwork for Schrödinger’s quantum mechanical model.
Practice Questions for JEE & NEET
- Calculate the ionization energy of a He⁺ ion in its ground state.
- Determine the wavelength of light emitted during the n=5 → n=2 transition in hydrogen.
- Find the total energy and radius of an electron in the fourth orbit of hydrogen.
- Compute the ratio of speeds of electrons in the first and third orbits.
- Evaluate the Rydberg constant using Bohr’s theoretical expressions.
FAQs
Q1. What is unique about Bohr’s atomic model?
It introduced quantized energy levels and angular momentum, making it the first theory to successfully explain hydrogen’s line spectrum.
Q2. Why do electrons not collapse into the nucleus?
According to Bohr, electrons occupy stable orbits where they do not emit radiation, preventing collapse.
Q3. How is the Bohr model applied in spectroscopy?
Each transition produces a photon of specific frequency, allowing identification of elements based on spectral lines.
Q4. How does Bohr’s model relate to modern quantum theory?
It paved the way for quantum mechanics by introducing quantization concepts that were later refined through wave-particle duality and Schrödinger’s equation.
Q5. What is the limitation of the Bohr model in modern applications?
It cannot explain complex spectra or behaviors of multi-electron atoms and fails under strong electromagnetic fields.
Conclusion
Bohr’s Model for the Hydrogen Atom remains one of the most influential theories in atomic physics. It provided a quantum explanation for atomic stability, energy quantization, and hydrogen’s spectral lines. Though later modified by quantum mechanics, Bohr’s principles still serve as a foundational concept for JEE and NEET aspirants. Understanding energy transitions, orbital quantization, and hydrogen spectral lines is vital for mastering both theoretical and numerical questions in modern atomic structure studies.










Get Social