Distance between Two Points in 3D Space – Class 11 Maths

Introduction

One of the most fundamental operations in geometry is finding the distance between two points. In two-dimensional (2D) coordinate geometry, we already studied the distance formula using the Pythagoras theorem. But in the real world, most objects exist in three dimensions (3D).

For example:

The distance between two airplanes flying at different altitudes.
The distance between a satellite and a ground station.
The distance between two atoms in a crystal.

In all such cases, we cannot limit ourselves to two coordinates (x, y); we must also consider the third coordinate (z). This is where the 3D distance formula comes in.

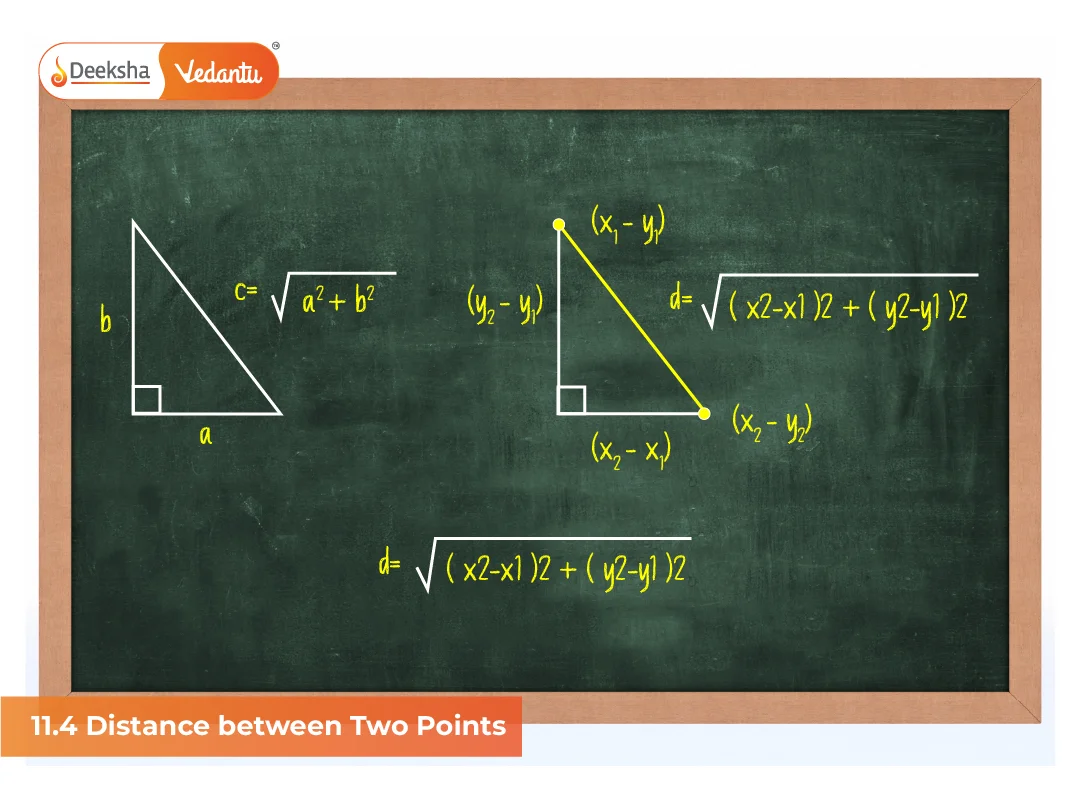
Recap: Distance Formula in 2D

If A(x₁, y₁) and B(x₂, y₂) are two points in a plane, then the distance between them is:

AB = √((x₂ – x₁)² + (y₂ – y₁)²)

This is derived using the Pythagoras theorem on a right triangle formed by horizontal and vertical differences.

Derivation of Distance Formula in 3D

Let A(x₁, y₁, z₁) and B(x₂, y₂, z₂) be two points in 3D space.

Drop perpendiculars from A and B onto the XY-plane.
- Let A’(x₁, y₁, 0) and B’(x₂, y₂, 0).
Distance between A and B can be split into:
- Horizontal distance in the XY-plane.
- Vertical difference in the z-coordinates.
First, calculate the distance in the XY-plane:
A’B’ = √((x₂ – x₁)² + (y₂ – y₁)²)
Now, include the difference in z-coordinates:
AB = √((A’B’)² + (z₂ – z₁)²)

Substituting A’B’:

AB = √((x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²)

This is the 3D Distance Formula.

Formula Recap

For points A(x₁, y₁, z₁) and B(x₂, y₂, z₂):

AB = √((x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²)

Special Cases

If z₁ = z₂:
- Points lie in the same plane parallel to XY-plane.
- Formula reduces to 2D form: AB = √((x₂ – x₁)² + (y₂ – y₁)²).
If y₁ = y₂:
- Formula reduces to AB = √((x₂ – x₁)² + (z₂ – z₁)²).
If x₁ = x₂:
- Formula reduces to AB = √((y₂ – y₁)² + (z₂ – z₁)²).

Thus, the 3D distance formula is a generalization of the 2D formula.

Geometric Interpretation

(x₂ – x₁), (y₂ – y₁), and (z₂ – z₁) are the differences in coordinates along x-, y-, and z-directions.
These form the edges of a rectangular box (cuboid).
The distance AB is the diagonal of the cuboid, calculated using Pythagoras theorem twice.

Solved Examples

Example 1: Basic Application

Find the distance between A(1, 2, 3) and B(4, 6, 8).

Solution:
AB = √((4 – 1)² + (6 – 2)² + (8 – 3)²)
= √(9 + 16 + 25)
= √50
= 5√2 units.

Example 2: Special Case

Find the distance between P(3, 5, 0) and Q(6, 9, 0).

Solution:
Since z₁ = z₂ = 0, points lie in XY-plane.
PQ = √((6 – 3)² + (9 – 5)²)
= √(9 + 16)
= √25 = 5 units.

Example 3: Distance from Origin

Find the distance of point A(7, –4, 5) from the origin.

Solution:
O(0, 0, 0), A(7, –4, 5)
OA = √((7 – 0)² + (–4 – 0)² + (5 – 0)²)
= √(49 + 16 + 25)
= √90 = 3√10 units.

Example 4: Midpoint Approach

Show that the midpoint of A(–2, 3, 1) and B(2, –1, 5) is equidistant from both points.

Solution:
Midpoint M = ((–2 + 2)/2, (3 + –1)/2, (1 + 5)/2) = (0, 1, 3).

AM = √((0 + 2)² + (1 – 3)² + (3 – 1)²) = √(4 + 4 + 4) = √12 = 2√3.
BM = √((2 – 0)² + (–1 – 1)² + (5 – 3)²) = √(4 + 4 + 4) = 2√3.

Thus, M is equidistant.

Example 5: Proving Collinearity

Show that points A(1, 2, 3), B(2, 3, 4), and C(3, 4, 5) are collinear.

Solution:
AB = √((2 – 1)² + (3 – 2)² + (4 – 3)²) = √3.
BC = √((3 – 2)² + (4 – 3)² + (5 – 4)²) = √3.
AC = √((3 – 1)² + (4 – 2)² + (5 – 3)²) = √12 = 2√3.

Since AB + BC = AC, the points are collinear.

Example 6: Opposite Vertices of Cube

Find the distance between opposite vertices of a cube of side 5 units.

Solution:
Cube diagonal formula = √(a² + a² + a²) = √(3a²) = a√3.
= 5√3 units.

Applications of Distance Formula in 3D

Physics:
- Distance between two particles.
- Position vector magnitude = distance from origin.
Engineering:
- Designing 3D structures, beams, bridges.
Computer Graphics:
- Collision detection in 3D gaming.
Astronomy:
- Distance between celestial bodies.
Exams (JEE/KCET/CBSE):
- Straightforward formula-based scoring questions.

Common Mistakes

Forgetting to include the z-coordinate difference.
Using wrong signs (especially in subtraction).
Confusing 2D formula with 3D.
Incorrectly simplifying square roots.

Practice Problems

Find the distance between P(–3, 2, 5) and Q(4, –1, –2).
Find the distance of (7, –2, 3) from origin.
Show that A(1, 2, 1), B(2, 3, 2), and C(3, 4, 3) are collinear.
A cube has side 6 cm. Find the length of its space diagonal.
Verify if the triangle with vertices (1, 0, 0), (0, 1, 0), (0, 0, 1) is equilateral.

Exam Weightage

CBSE Boards: 3–4 marks (distance/midpoint/collinearity problems).
JEE Main: 1–2 questions (distance between points, collinearity, cube diagonals).
KCET/COMEDK: 1–2 MCQs (distance/midpoint).

This section is usually direct and scoring.

FAQs

Q1. What is the 3D distance formula?
For A(x₁, y₁, z₁) and B(x₂, y₂, z₂): √((x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²).

Q2. How is it derived?
Using the Pythagoras theorem extended to 3D space.

Q3. Is distance from origin a special case?
Yes, if one point is (0, 0, 0).

Q4. Can this be used for proving collinearity?
Yes. If AB + BC = AC, the points are collinear.

Q5. Is the 3D distance formula used in physics?
Yes, for particle motion, vectors, and displacement.

Conclusion

The distance formula in 3D is a direct extension of the 2D formula, incorporating the difference in z-coordinates as well. It allows us to calculate distances between any two points in space using just their coordinates.

This topic has wide-ranging applications in mathematics, physics, engineering, and computer graphics. For students, it is one of the most scoring areas in exams, since questions are straightforward and formula-based.

Mastery of this formula, along with practice in collinearity, midpoints, and space diagonals, ensures confidence in tackling 3D geometry problems in both board exams and competitive exams like JEE, KCET, and COMEDK.