4. Complex Numbers and Quadratic Equations – Class 11 Mathematics

Introduction

Mathematics often deals with solving equations. At the Class 10 level, you encountered quadratic equations and learned how to solve them using factorization, completing the square, and the quadratic formula. However, there was always a limitation: when the discriminant of a quadratic was negative, we said that the equation had “no real solution.”

Class 11 expands this horizon. Instead of stopping at “no solution,” we now extend the number system to include a new kind of number: the complex number. This chapter, based on NCERT Class 11 Mathematics, introduces the concept of complex numbers and their properties. For JEE, KCET, and COMEDK aspirants, mastery of complex numbers is essential, since these appear in algebra, trigonometry, coordinate geometry, and even higher topics like calculus.

The chapter is structured into four main parts:

• 4.2 Complex Numbers – Definition, motivation, and standard form.
• 4.3 Algebra of Complex Numbers – Operations such as addition, subtraction, multiplication, and division.
• 4.4 Modulus and Conjugate – Two essential tools that simplify manipulation of complex numbers.
• 4.5 Argand Plane and Polar Representation – Geometrical representation and polar form (Euler’s approach).

Before diving into each, let’s understand the motivation behind introducing complex numbers.

Why Do We Need Complex Numbers?

Take the quadratic equation:
x² + 1 = 0

If you try solving, you get:
x² = −1 → x = √(−1)

But in the set of real numbers, the square root of −1 doesn’t exist. To handle this, mathematicians extended the number system by defining a new unit i, such that:

i² = −1

Thus, √(−1) is denoted by i, and we can write solutions like x = ±i.

This extension ensures all quadratic equations have solutions, either in real numbers or in complex numbers. The set of complex numbers is written as:

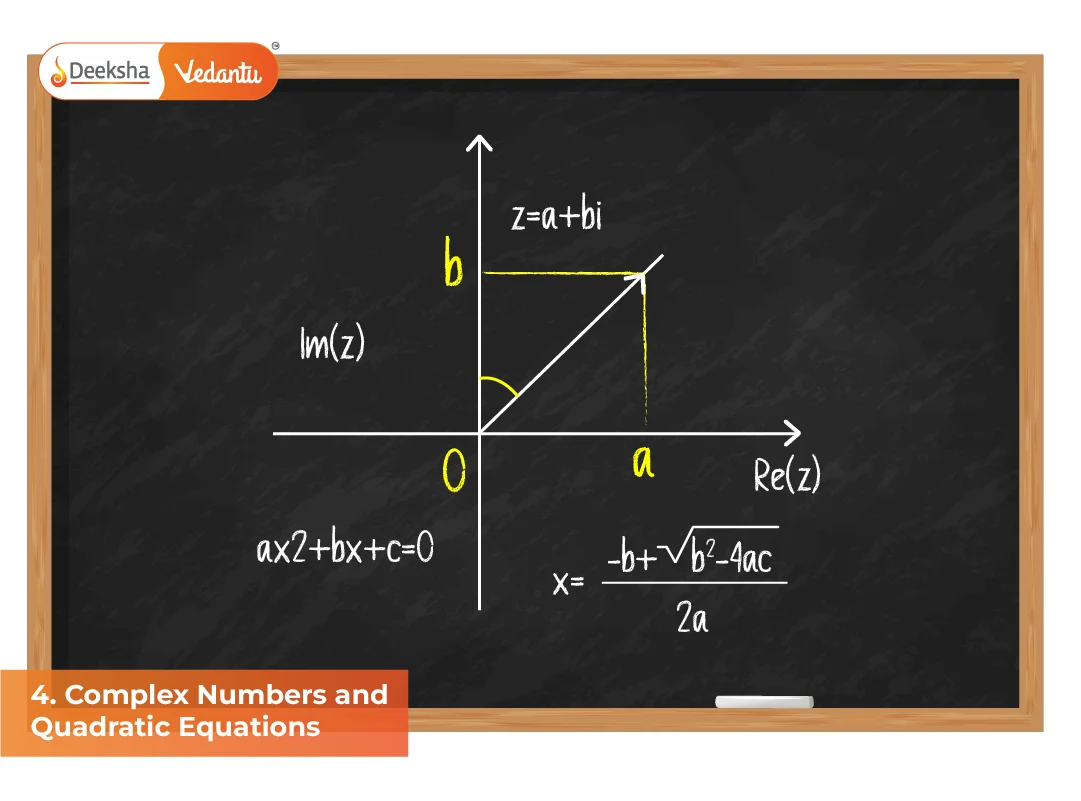
z = a + ib, where
a = real part (Re(z))
b = imaginary part (Im(z))

Subtopic Briefs

4.2 Complex Numbers

This section introduces the basic definition of a complex number. Every complex number can be expressed in the form a + ib, where a and b are real numbers, and i² = −1. The concept generalizes real numbers (where b = 0) and purely imaginary numbers (where a = 0).

Example:
z = 3 + 4i → real part = 3, imaginary part = 4

In JEE/KCET, questions may ask you to identify real/imaginary parts, determine equalities, or evaluate simple powers of i (noting the cycle: i, −1, −i, 1).

4.3 Algebra of Complex Numbers

Complex numbers can be added, subtracted, multiplied, and divided, similar to real numbers, but with i² = −1 guiding simplification.

Examples:
(2 + 3i) + (4 − 5i) = 6 − 2i
(2 + 3i)(1 − 2i) = 2 − 4i + 3i − 6i² = 2 − i + 6 = 8 − i

This section also covers properties such as associativity, distributivity, and commutativity. Division of complex numbers often requires multiplying numerator and denominator by the conjugate.

4.4 The Modulus and the Conjugate of a Complex Number

For z = a + ib:

• Modulus: |z| = √(a² + b²) → represents the distance of z from the origin in the Argand plane.
• Conjugate: z̅ = a − ib → useful for simplification and rationalization.

Important identity:
z × z̅ = |z|²

This identity is heavily used in both board exam proofs and JEE problems.

4.5 Argand Plane and Polar Representation

Complex numbers can also be represented as points in a plane:

• x-axis → real part
• y-axis → imaginary part

This is called the Argand plane. The modulus gives the distance from the origin, while the argument (θ) gives the angle made with the positive x-axis.

Thus, a complex number can be written in polar form:
z = r (cos θ + i sin θ), where r = |z|

Using Euler’s formula:
z = r e(iθ)

This polar form simplifies multiplication and division of complex numbers, since:
z₁z₂ = r₁r₂ e(i(θ₁+θ₂))

This property makes polar representation extremely powerful in competitive exams.

Worked-Out Examples

Example 1:
Solve x² + 1 = 0
x = ±i

Example 2:
Simplify (1 + i)²
= 1 + 2i + i² = 2i

Example 3:
Find modulus and conjugate of z = 3 + 4i
|z| = √(3² + 4²) = 5
z̅ = 3 − 4i

Example 4:
Write 1 + i in polar form
r = √(1² + 1²) = √2
θ = tan⁻¹(1/1) = 45°
So, z = √2 (cos 45° + i sin 45°)

JEE / KCET / COMEDK Relevance

• JEE often asks problems involving simplification, properties of conjugates, or using De Moivre’s theorem (an extension of polar form).
• KCET/COMEDK tends to focus on standard manipulations: evaluating powers of i, solving quadratic equations with negative discriminants, and basic polar conversions.
• Quick application of conjugate and modulus properties helps reduce calculation time.

Common Pitfalls

• Forgetting that i² = −1 → common cause of sign errors.
• Confusing modulus (always non-negative) with real/imaginary parts.
• Mixing up conjugate signs.
• Incorrectly identifying argument θ (especially in 2nd, 3rd, and 4th quadrants).

Strategy Tips

1. Always reduce powers of i using the cycle (i, −1, −i, 1).
2. For division, multiply numerator and denominator by the conjugate.
3. When solving quadratics with negative discriminants, directly apply:
   Roots = (−b ± √(b² − 4ac)) / 2a,
   and simplify √(negative) as i√(positive).
4. In polar form, use multiplication/division to quickly compute results.

FAQs

Q1: What is the standard form of a complex number?
It is a + ib, where a and b are real numbers, and i² = −1.

Q2: Why are complex numbers needed?
They allow solutions to equations like x² + 1 = 0, which have no real roots.

Q3: What is the difference between modulus and conjugate?
Modulus is the distance from the origin (non-negative real number), while conjugate is obtained by changing the sign of the imaginary part.

Q4: How are complex numbers used in JEE/KCET?
They are used in algebra, trigonometry, and solving equations, and often appear in questions requiring quick simplification.

Q5: Is polar representation important?
Yes, because it simplifies multiplication/division and links complex numbers to trigonometry.

Summary and Key Takeaways

• Complex numbers extend the real number system to include √(−1).
• Standard form is a + ib.
• Algebra of complex numbers mirrors real numbers but follows i² = −1.
• Modulus gives distance, conjugate helps simplify.
• Argand plane offers a geometric view; polar form gives computational power.
• Essential for both board exams and competitive exams (JEE, KCET, COMEDK).