4.5 Argand Plane and Polar Representation – Class 11 Mathematics

Introduction

Complex numbers are not just algebraic entities; they have a beautiful geometrical interpretation. When we step into the Argand plane and use polar representation, the abstract world of “i” suddenly becomes a visual and calculable space. This transformation is not only aesthetically pleasing but also practically essential in advanced problem-solving.

For students preparing for JEE, KCET, and COMEDK, mastering this topic provides a huge advantage. Many questions – ranging from simple conversions to applications of De Moivre’s theorem and roots of unity – appear in these exams. This makes understanding the Argand plane and polar representation indispensable.

Argand Plane: The Geometric World of Complex Numbers

Representation

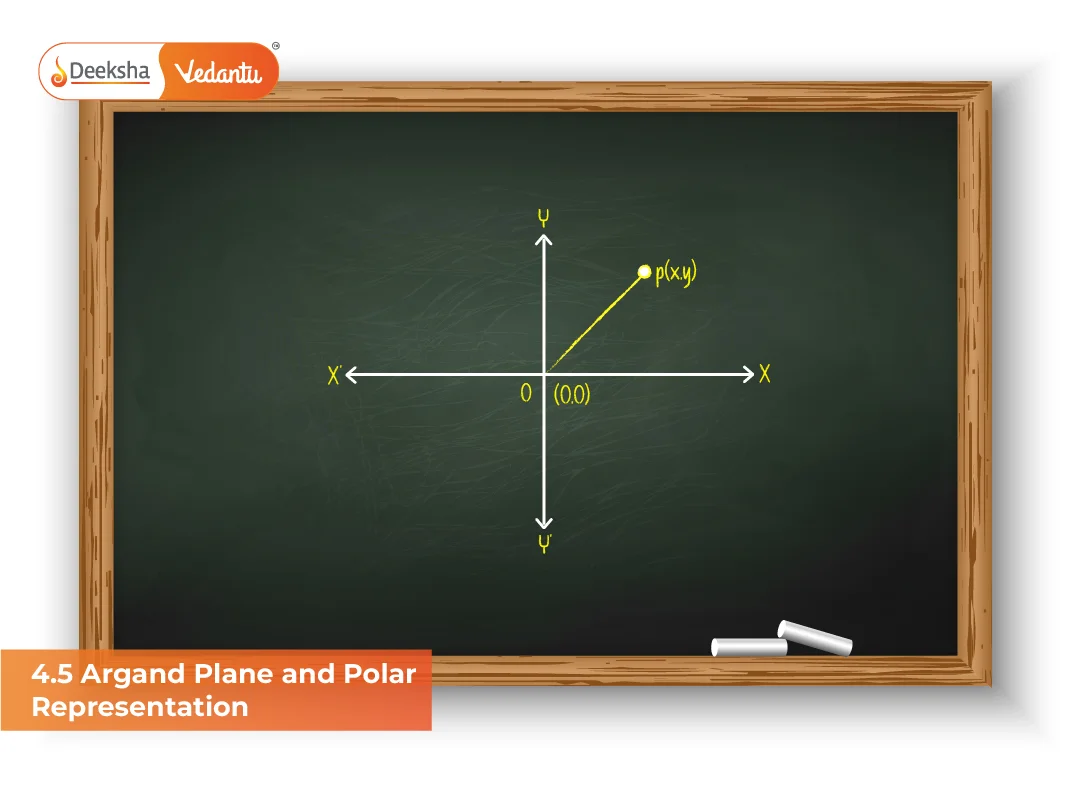
• A complex number z = a + ib can be represented as the ordered pair (a, b).
• Plotting this on a plane:
  • Horizontal axis = Real axis
  • Vertical axis = Imaginary axis
• The plane is called the Argand plane (after Jean-Robert Argand).

Example

z = 3 + 4i → plotted as point (3, 4).
This point can also be visualized as the vector OP, where O is the origin and P is (3, 4).

Modulus and Argument

Modulus (r)

The distance of point (a, b) from the origin:
r = √(a² + b²).

Example: For z = 3 + 4i,
r = √(3² + 4²) = √25 = 5.

Argument (θ)

The angle between the line OP and the positive x-axis:
θ = tan⁻¹(b/a), with quadrant adjustments.

Example: For z = 3 + 4i,
θ = tan⁻¹(4/3) ≈ 53.13°.

Thus, every complex number is uniquely determined by (r, θ).

Polar Representation of Complex Numbers

Any complex number z = a + ib can be expressed as:

z = r (cos θ + i sin θ)

where,

• r = modulus
• θ = argument

This is the polar form of a complex number.

Euler’s Formula and Exponential Form

Leonhard Euler gave the most elegant relation:
e(iθ) = cos θ + i sin θ.

Thus, the polar form can be written compactly as:
z = r e(iθ).

This form is extremely powerful and forms the foundation for De Moivre’s theorem, powers, and roots.

Conversion Between Forms

Rectangular → Polar

1. z = a + ib
2. r = √(a² + b²), θ = tan⁻¹(b/a)
3. z = r (cos θ + i sin θ).

Polar → Rectangular

z = r (cos θ + i sin θ)
= r cos θ + i r sin θ
= a + ib.

Properties of Polar Representation

1. Multiplication
   z₁ = r₁ e(iθ₁), z₂ = r₂ e(iθ₂)
   z₁z₂ = r₁r₂ e(i(θ₁+θ₂))
   (Magnitudes multiply, angles add).
2. Division
   z₁/z₂ = (r₁/r₂) e(i(θ₁−θ₂))
   (Magnitudes divide, angles subtract).
3. Powers (De Moivre’s Theorem)
   (cos θ + i sin θ)ⁿ = cos(nθ) + i sin(nθ).
4. Roots
   Every complex number has n distinct nth roots:
   z(1/n) = r(1/n) [cos((θ + 2kπ)/n) + i sin((θ + 2kπ)/n)], k = 0,1,…,(n−1).

Geometric Interpretation

• Multiplication → rotates and scales vectors.
• Division → shrinks/expands and rotates backward.
• Raising to powers → multiple rotations and stretching.
• Roots → equally spaced points on a circle.

Example: Cube roots of unity

Equation: z³ = 1 → in polar form, 1 = e(i2kπ), k = 0,1,2.
Roots: z = e(i2kπ/3).

These correspond to points on the unit circle at 120° intervals.

Solved Examples

Example 1: Convert to polar form

z = −1 + i√3.

r = √((-1)² + (√3)²) = √(1 + 3) = 2.
θ = tan⁻¹(√3/−1). Since (a = −1, b = √3), the point lies in the 2nd quadrant.
Thus θ = 120° = 2π/3.
So, z = 2 (cos 120° + i sin 120°).

Example 2: Multiplication using polar form

z₁ = 2 e(i30°), z₂ = 3 e(i45°).
z₁z₂ = 6 e(i(30°+45°)) = 6 e(i75°).

Example 3: Find cube roots of unity

We want solutions to z³ = 1.
Polar form of 1: e(i2kπ), k = 0,1,2.
So, roots: z = e(i2kπ/3).
That gives: 1, (−1/2 + i√3/2), (−1/2 − i√3/2).

Example 4 (JEE type): Solve z⁴ = 1

Polar form: 1 = e(i2kπ), k = 0,1,2,3.
Roots: z = e(i2kπ/4).
= e(i0), e(iπ/2), e(iπ), e(i3π/2).
So, z = 1, i, −1, −i.

Applications in JEE, KCET, COMEDK

1. Conversion Questions (Boards/JEE Main):
   • Write 1 + i√3 in polar form.
   • Express cos θ + i sin θ in exponential form.
2. De Moivre’s Theorem (JEE Mains/Advanced):
   • Expand (cos θ + i sin θ)ⁿ.
   • Find exact values like cos(5π/12).
3. Roots of Unity (KCET/COMEDK):
   • Solve zⁿ = 1.
   • Geometric interpretation of nth roots.

Practice Problems

1. Convert z = 1 − i√3 into polar form.
2. Multiply z₁ = 2(cos 30° + i sin 30°) and z₂ = 3(cos 60° + i sin 60°).
3. Find the fourth roots of unity.
4. Solve z³ = 8 (in exponential form).
5. Prove that the cube roots of unity form the vertices of an equilateral triangle.

Answers (Quick)

1. r = 2, θ = −60°. So, z = 2 (cos −60° + i sin −60°).
2. Result = 6 (cos 90° + i sin 90°) = 6i.
3. Roots: 1, i, −1, −i.
4. 8 = 2³ → in polar form: 8 e(i2kπ). Roots: 2 e(i2kπ/3), k = 0,1,2.
5. By geometry, arguments are 0°, 120°, 240° → equilateral triangle.

Common Mistakes to Avoid

• Quadrant errors: Always check which quadrant (a, b) lies in before assigning θ.
• Forgetting multiple roots: nth root means n different answers, not just one.
• Skipping Euler’s form: Many exam problems become easier with z = re(iθ).
• Sign mistakes in θ: tan⁻¹ only gives principal values; adjust to correct quadrant.

Summary

• Complex numbers can be plotted in the Argand plane as (a, b).
• Modulus = √(a² + b²), Argument = tan⁻¹(b/a).
• Polar form: z = r (cos θ + i sin θ).
• Euler’s form: z = r e(iθ).
• Multiplication, division, powers, and roots are simplified in polar form.
• Geometric interpretation: rotations and scaling in the plane.
• Essential for De Moivre’s theorem and roots of unity.