2.6 Quantum Mechanical Model of the Atom – Class 11 Chemistry

Introduction

The Quantum Mechanical Model of the Atom stands as the most advanced and accurate theory for understanding atomic structure and electron behavior. It merges the revolutionary ideas of wave-particle duality, Heisenberg’s Uncertainty Principle, and Schrödinger’s Wave Equation to form a unified mathematical and conceptual framework. Unlike earlier models that viewed electrons as particles orbiting the nucleus in fixed circular paths, this model views electrons as waves existing in regions of space called orbitals, where the likelihood of finding an electron is highest.

This transition from deterministic orbits to probabilistic orbitals marked a paradigm shift in atomic theory, giving rise to quantum mechanics, which now forms the foundation of modern physics and chemistry. It helps explain not only atomic spectra and bonding but also molecular behavior, periodic trends, and even phenomena at the nanoscale.

Foundation of the Quantum Mechanical Model

The development of the quantum mechanical model was the culmination of several fundamental discoveries:

1. Wave-Particle Duality: Proposed by Louis de Broglie, this principle states that all matter exhibits both particle and wave characteristics. Electrons, like photons, can behave as waves under certain conditions, giving rise to the concept of matter waves.
2. Heisenberg’s Uncertainty Principle: Werner Heisenberg formulated that it is impossible to know both the exact position and momentum of an electron at the same time. This introduced a probabilistic understanding of atomic behavior and invalidated the idea of well-defined electron orbits.
3. Schrödinger’s Wave Equation: Erwin Schrödinger developed a mathematical equation that described the motion of an electron as a wave. The solutions to this equation revealed quantized energy levels and spatial distributions known as orbitals. 

These principles together provided a model capable of explaining not only hydrogen’s atomic spectrum but also the behavior of electrons in multi-electron atoms, something Bohr’s theory could not achieve.

Schrödinger’s Wave Equation and Its Significance

In 1926, Erwin Schrödinger introduced his famous equation:

Hψ = Eψ

Where:

• H = Hamiltonian operator (represents total energy of the system)
• ψ = wave function of the electron
• E = quantized energy associated with the electron state

This equation provides a mathematical representation of how electrons behave as waves within atoms. The wave function (ψ) contains all information about the electron’s energy and spatial distribution, while ψ² (the square of the wave function) gives the probability density — the likelihood of finding an electron in a particular region around the nucleus.

Importance of the Schrödinger Equation

• It replaces Bohr’s circular orbits with orbitals, regions of space where electrons are most likely to be located.
• It accurately describes quantized energy levels for simple systems like hydrogen.
• The mathematical solutions yield distinct orbital shapes and orientations that align with experimental observations.
• It lays the groundwork for chemical bonding theories such as Molecular Orbital Theory and Valence Bond Theory.

Example (Hydrogen Atom)

For the hydrogen atom, solving Schrödinger’s equation gives discrete energy levels that match Bohr’s predictions but adds a new layer of detail — the probability distribution and shape of the orbital. Thus, quantum mechanics not only supports Bohr’s quantization concept but also expands on it.

Quantum Numbers and Their Significance

Each solution to Schrödinger’s equation is defined by a unique set of quantum numbers, which collectively describe every electron in an atom:

1. Principal Quantum Number (n): Defines the main energy level or shell of an electron. Larger n values mean higher energy and a greater average distance from the nucleus.
2. Azimuthal Quantum Number (l): Determines the subshell or orbital shape (s, p, d, f). It can have integer values from 0 to (n–1).
3. Magnetic Quantum Number (m): Specifies the orientation of the orbital in three-dimensional space. Its values range from –l to +l.
4. Spin Quantum Number (s): Represents the electron’s intrinsic spin, either +½ or –½.

These quantum numbers act like coordinates, identifying each electron’s energy, location, and spin direction. Together, they ensure that no two electrons in an atom can share the same quantum state, as per the Pauli Exclusion Principle.

Example Problem

Q: For an electron with n = 3 and l = 1, find possible values of m and s.
A: Since l = 1, m = –1, 0, or +1, and s = ±½.

Application in JEE/NEET

Students should learn how these quantum numbers relate to electron configurations, orbital diagrams, and periodic properties. Common exam problems include identifying valid sets of quantum numbers or calculating the number of orbitals in a given shell (using n²).

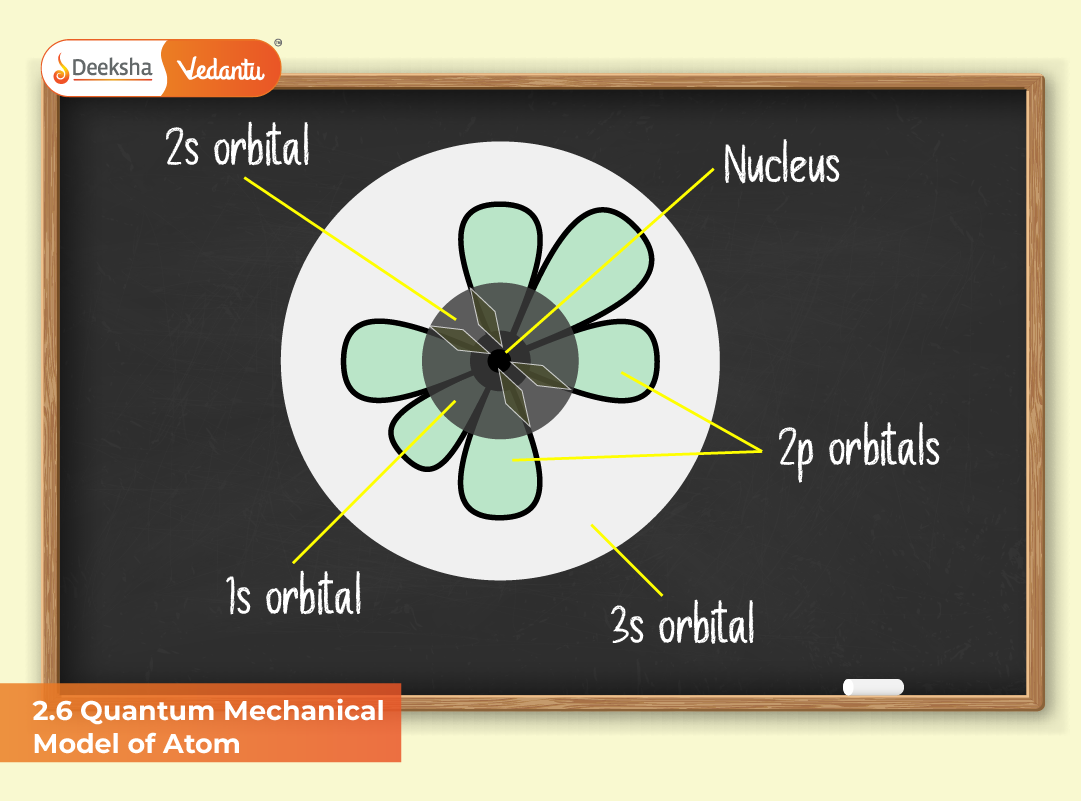
Shapes and Characteristics of Atomic Orbitals

The shape and structure of an orbital depend on the azimuthal quantum number (l):

• s-orbitals (l = 0): Spherical, with high electron density at the nucleus. Probability distribution depends only on distance from the nucleus.
• p-orbitals (l = 1): Dumbbell-shaped and oriented along the x, y, or z axes (px, py, pz). Each orbital can hold two electrons with opposite spins.
• d-orbitals (l = 2): Cloverleaf-shaped orbitals with more complex nodal planes, contributing significantly to transition metal chemistry.
• f-orbitals (l = 3): Intricate shapes with multiple lobes, relevant for lanthanides and actinides.

Nodal Structure

Orbitals may contain nodes, regions where the probability of finding an electron is zero. The number of nodes equals (n – 1). Nodes can be radial (spherical) or angular (planar) depending on the orbital type.

Example Insight

In the hydrogen atom, the 2s orbital has one radial node, while the 2p orbital has none. This explains why electrons in 2p orbitals are, on average, farther from the nucleus than those in 2s orbitals.

Major Postulates of the Quantum Mechanical Model

1. Electrons behave as standing waves, described by wave functions (ψ) that contain all information about their state.
2. Probability distribution (ψ²) defines where an electron is likely to be found, replacing the concept of fixed orbits.
3. Energy quantization arises naturally from boundary conditions in Schrödinger’s equation.
4. Orbitals replace orbits — electrons occupy 3D regions instead of flat paths.
5. Quantum numbers define energy, shape, orientation, and spin of each electron.
6. Pauli Exclusion Principle: No two electrons in the same atom have identical quantum numbers.
7. The model successfully explains atomic spectra, periodic properties, and the basis of chemical bonding.

Limitations and Extensions

Although the quantum mechanical model is highly successful, it still has some limitations:

• It cannot perfectly account for electron-electron interactions in multi-electron atoms without approximation methods.
• Relativistic corrections are not part of Schrödinger’s original framework but are handled by Dirac’s relativistic quantum mechanics.
• Modern computational models, including Density Functional Theory (DFT) and Hartree-Fock methods, build upon this model for more complex systems.

Applications in JEE/NEET and Real-World Science

• Determining the number and type of orbitals for given quantum numbers.
• Understanding nodal planes and shapes of orbitals.
• Predicting atomic structure and periodic trends.
• Applying principles to chemical bonding and spectroscopy.
• Relating wave function probability to electron cloud density.

Practice Problems

1. Calculate the total number of orbitals when n = 4.
2. Explain why ψ² is used instead of ψ to describe electron distribution.
3. For n = 3 and l = 2, list all possible m values.
4. Derive the relationship between the principal quantum number and orbital count.
5. Justify why two electrons in an atom cannot have the same set of four quantum numbers.

FAQs

Q1. What is the fundamental idea behind the quantum mechanical model?

It is based on the principle that electrons behave like waves and their exact position and momentum cannot be simultaneously determined. Instead, their behavior is defined probabilistically through the wave function ψ.

Q2. How are orbitals different from orbits?

Orbits are fixed circular paths from Bohr’s model, while orbitals are three-dimensional regions where electrons are most likely to be found.

Q3. What do quantum numbers signify in an atom?

They describe the energy level, shape, orientation, and spin of an electron, allowing each electron to be uniquely identified.

Q4. What is ψ² in the context of atomic theory?

ψ² represents the probability density of finding an electron at a particular point in space around the nucleus.

Q5. Why is Schrödinger’s equation so significant?

Because it provides a complete mathematical framework for understanding atomic and molecular structures, explaining quantized energies, and predicting chemical behavior.

Conclusion

The Quantum Mechanical Model of the Atom revolutionized our understanding of atomic and subatomic behavior. It replaced the rigid, circular orbits of Bohr’s theory with a dynamic, probability-based concept of orbitals, where electrons exist as waves confined to specific energy states. This model not only explains atomic spectra and bonding but also forms the basis for quantum chemistry, molecular physics, and materials science. For JEE and NEET aspirants, mastering this topic is crucial to grasping key ideas about electronic configuration, periodicity, and quantum theory that form the core of advanced chemistry and physics.