Geometry is more than just shapes and figures – it’s the mathematical language of space, dimensions, and structure. From calculating the area of a triangle to proving congruence and similarity, mastering the basics of geometry is essential for Class 10 students aiming to excel in their exams.
This blog is your complete guide to the most important geometry basics, including theorems, formulas, practical applications, proofs, and visual explanations designed to simplify learning and reinforce your understanding. We’ll also dive into how geometry shapes our physical world and trains your brain to think critically.
Introduction to Geometry: Why It Matters
Geometry is the study of shapes, sizes, angles, dimensions, and their relationships in space. It forms the basis of architecture, design, engineering, astronomy, robotics, urban planning, and even computer graphics.
In Class 10, geometry is more than an academic subject. It develops logical thinking, enhances visual-spatial understanding, and nurtures problem-solving abilities that go beyond textbooks. Whether you’re planning to become an architect or preparing for board exams, a strong command of geometry is foundational.

Geometry Basics Every Student Should Know
Before diving into complex theorems or solving tricky problems, ensure your foundation is strong. Here are the essential geometry basics:
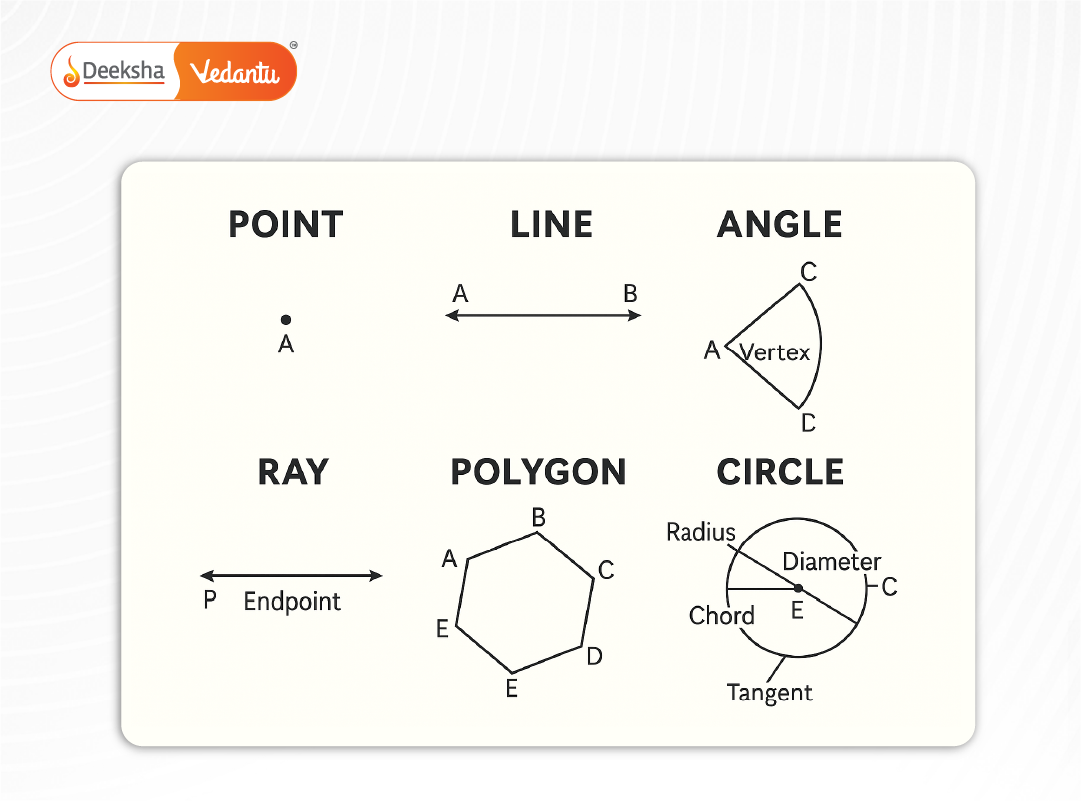
Key Geometric Terms
- Point: A location in space with no dimension
- Line: A straight one-dimensional figure with infinite length
- Line Segment: A part of a line with two endpoints
- Ray: A line that starts at a point and extends infinitely
- Angle: Formed when two rays meet at a common endpoint (vertex)
- Polygon: A closed figure with straight sides (e.g., triangle, square)
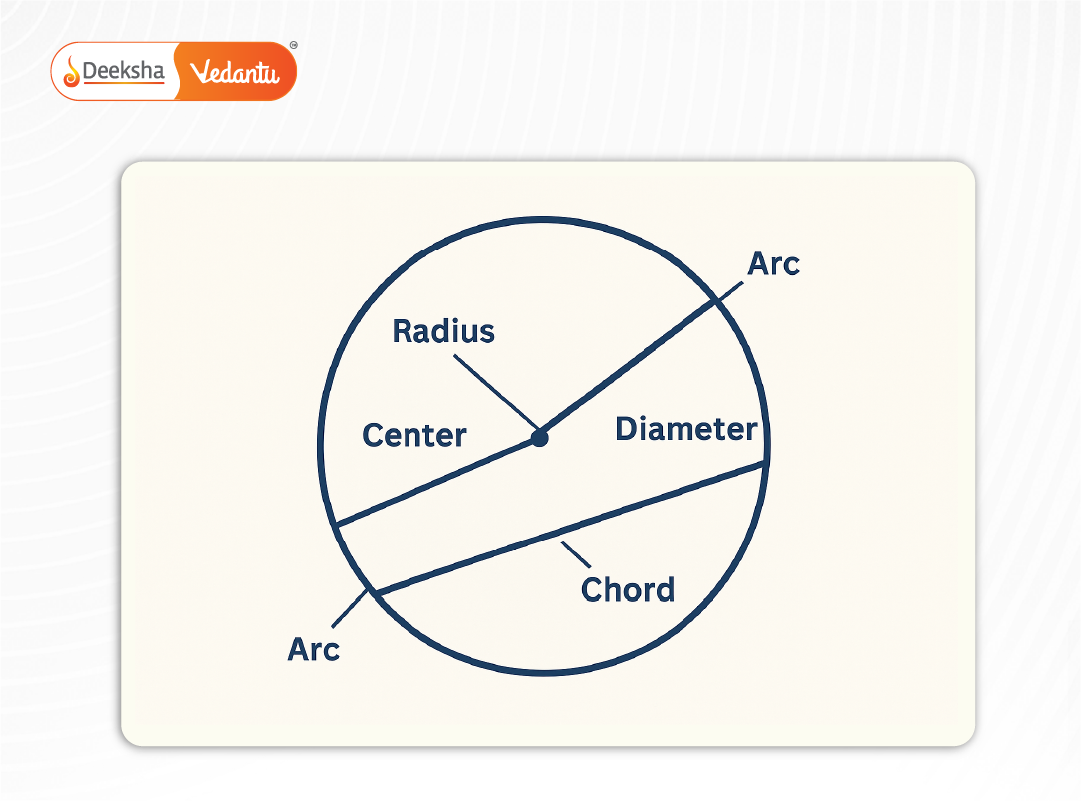
- Circle: A set of points equidistant from a central point
- Chord: A line segment joining two points on a curve
Types of Angles
- Acute Angle: Less than 90°
- Right Angle: Exactly 90°
- Obtuse Angle: More than 90° but less than 180°
- Straight Angle: Exactly 180°
- Reflex Angle: Greater than 180° but less than 360°
- Full Angle: Exactly 360°
Understanding these terms helps students approach geometric diagrams, proofs, and numerical questions with confidence. Always label figures and apply definitions consistently in constructions and proofs.
Important Geometry Formulas Class 10
Knowing the geometry formulas for Class 10 is key to solving problems quickly and accurately. These formulas will appear repeatedly in exam questions and real-life scenarios.
Triangle Formulas
- Area of Triangle (Heron’s Formula):
where - Area of Triangle (Standard):
- Equilateral Triangle Area:
Perimeter Formulas
- Perimeter of Triangle:
- Perimeter of Rectangle:
- Perimeter of Square:

Circle Formulas
- Circumference:
- Area:
Understanding Triangles: Foundation of Geometry
Triangles form the core of several geometry topics. Mastering them helps in solving questions from multiple chapters, including trigonometry, coordinate geometry, and mensuration.
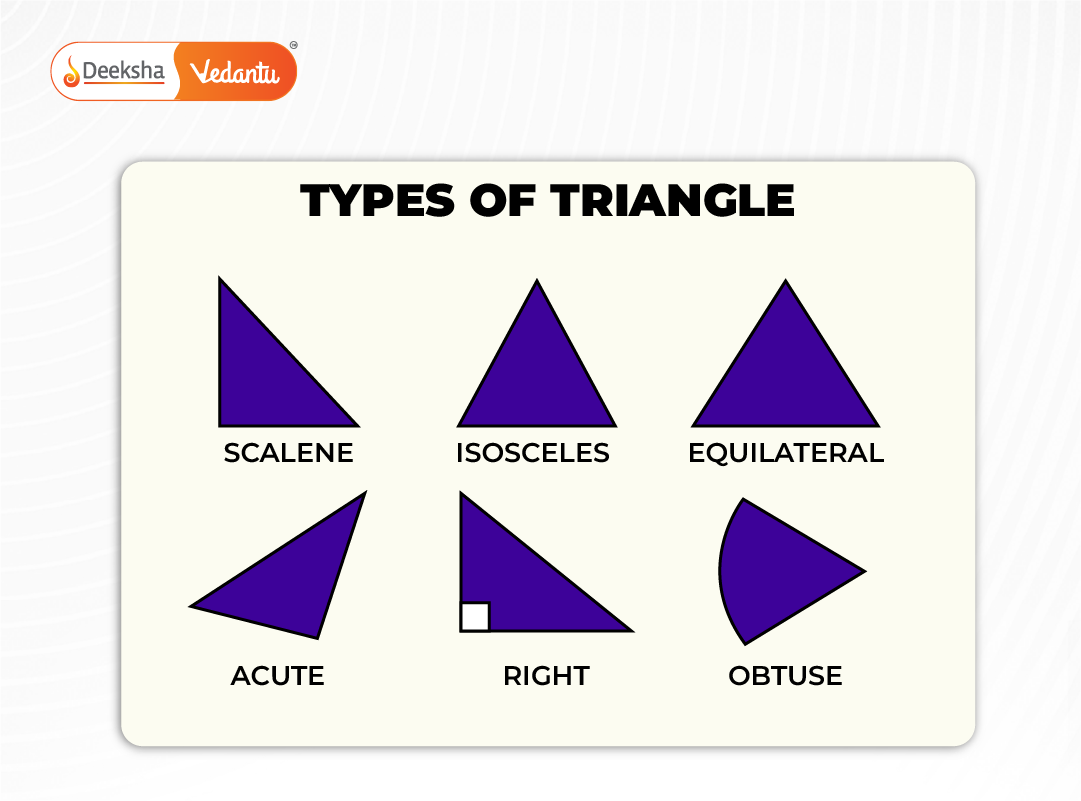
Types of Triangles
- Based on Sides:
- Equilateral: All sides equal, all angles 60°
- Isosceles: Two sides equal, two angles equal
- Scalene: All sides and angles different
- Based on Angles:
- Acute Triangle: All angles less than 90°
- Right Triangle: One angle is 90°
- Obtuse Triangle: One angle greater than 90°
Introduction to Triangles – Learn more
Properties of Triangles
- Sum of interior angles = 180°
- Exterior angle = sum of opposite interior angles
- Triangle inequality theorem: Sum of two sides > third side
- Angle opposite the longer side is greater
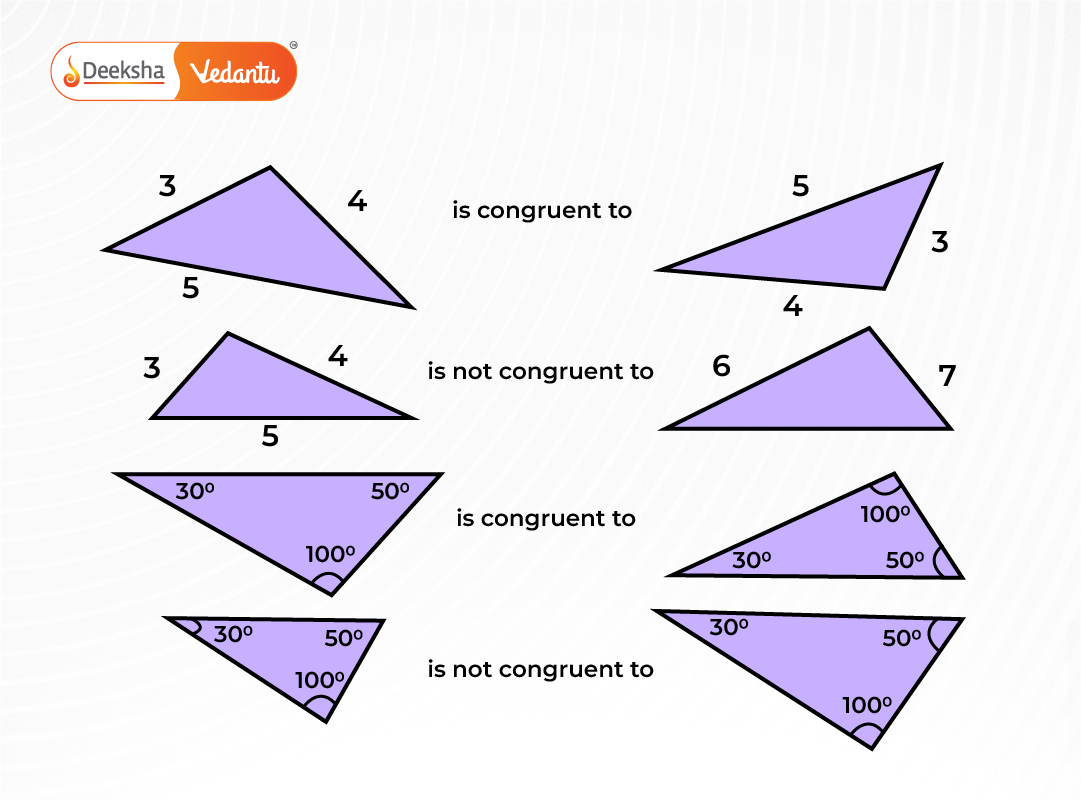
Congruence of Triangles
Congruent triangles have the same size and shape. They match in all sides and angles and can be placed over each other perfectly.
Congruence Criteria
- SSS (Side-Side-Side)
- SAS (Side-Angle-Side)
- ASA (Angle-Side-Angle)
- AAS (Angle-Angle-Side)
- RHS (Right angle-Hypotenuse-Side)
Applications
- Constructing identical geometric shapes
- Engineering and blueprint measurements
- Geometry proofs and justifications in exams
Similarity of Triangles
While congruent triangles are identical in size, similar triangles have the same shape but can differ in size. Their corresponding angles are equal, and sides are in proportion.
Similarity Criteria
- AAA (Angle-Angle-Angle)
- SSS (Side-Side-Side in proportion)
- SAS (Side-Angle-Side in proportion)
Read about Similarity of Triangles To understand the specific conditions under which triangles are considered similar, it’s helpful to explore the formal criteria.
Also see: Criteria for Similarity
Applications
- Measuring inaccessible heights (e.g., trees or buildings using shadows)
- Maps and scale drawings
- Trigonometry: deriving ratios like sine and cosine
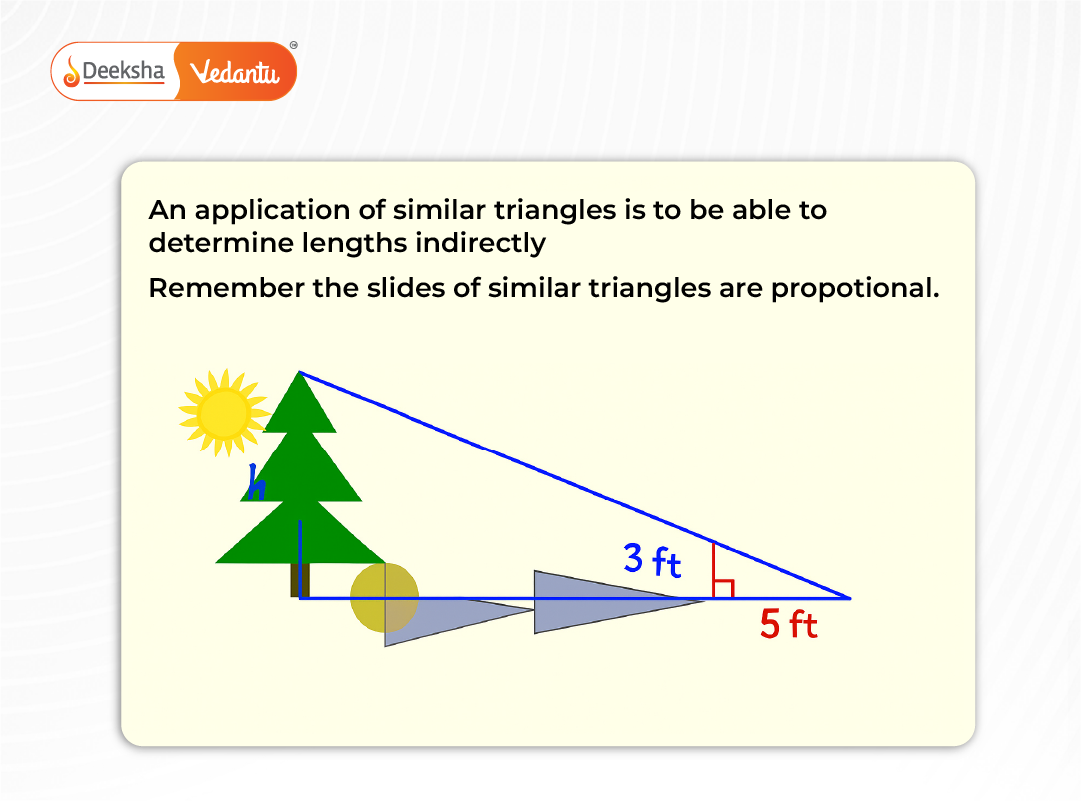
Area and Perimeter Geometry Applications
Why It Matters
Understanding area and perimeter geometry helps solve practical problems – like fencing a garden, tiling a floor, calculating paint required, or budgeting for building construction.
Real-World Examples
- Area of land plots (triangles, rectangles)
- Perimeter for fencing and boundary walls
- Circle area for landscaping or circular pools
- Floor tiling and wall painting estimates
Tips to Solve Area/Perimeter Questions
- Visualize and draw the shape
- Label dimensions clearly
- Apply correct formula
- Watch unit conversions (cm² vs m², etc.)
Geometry Theorems Explained for Students
Class 10 geometry includes several theorems that form the backbone of exam questions.
Key Theorems
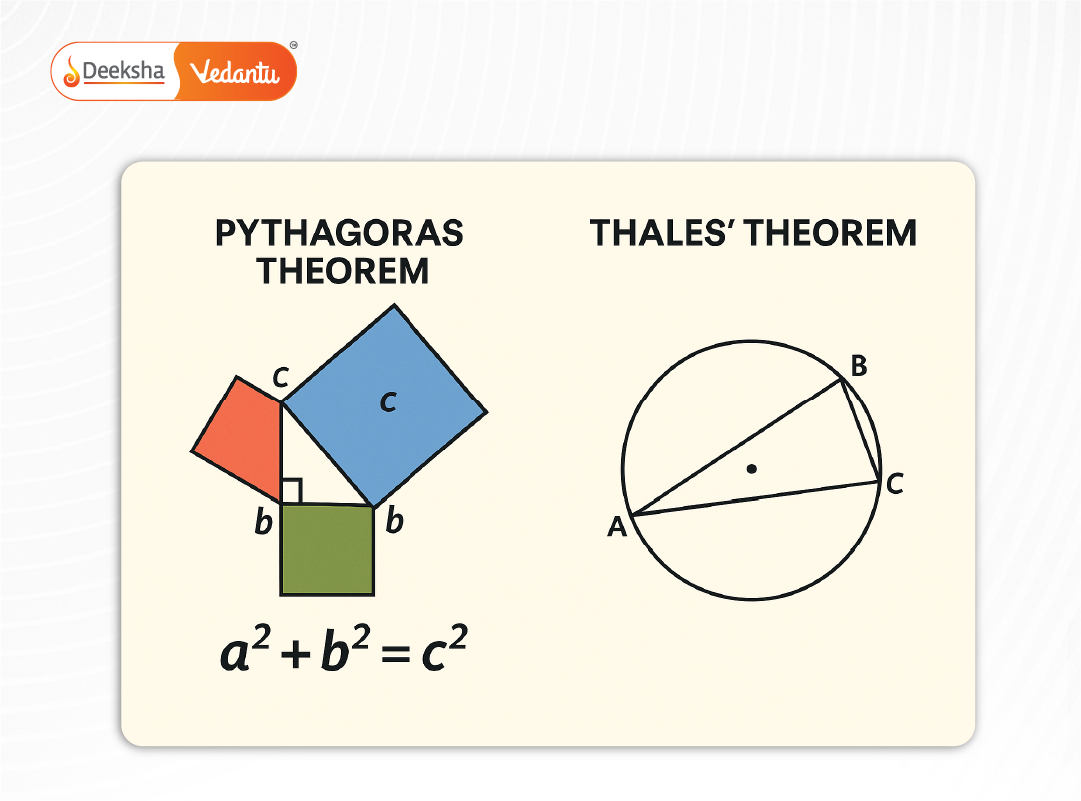
- Pythagoras Theorem: In a right triangle,
- Basic Proportionality Theorem (Thales): A line drawn parallel to one side of a triangle divides the other two sides proportionally
- Midpoint Theorem: The line joining midpoints of two sides of a triangle is parallel to the third side and half its length
- Angle Bisector Theorem: Angle bisector divides the opposite side in the ratio of adjacent sides
 .
.
Tips to Remember Theorems
- Draw and label diagrams step-by-step
- Understand each step in the proof
- Relate theorems to real-world examples
- Practice questions using NCERT and sample papers
FAQs About Geometry for Class 10
1. What are the most important geometry concepts in Class 10?
Focus on triangles, similarity, congruence, Pythagoras theorem, all area and perimeter formulas, and theorem-based proofs.
2. How can I remember geometry formulas better?
Use flashcards, create a formula wall chart, revise daily, and apply them in practice problems.
3. What’s the difference between congruent and similar triangles?
Congruent triangles are identical in size and shape. Similar triangles have the same shape but different sizes, with proportional sides and equal angles.
4. Why is geometry important in real life?
From construction and design to navigation, art, and even robotics – geometry helps solve real-world problems efficiently and creatively.
5. How should I prepare for geometry questions in exams?
Understand concepts first, revise all theorems and formulas, solve previous years’ questions, draw diagrams neatly, and justify every step in proofs.
Conclusion
Mastering geometry involves more than rote learning – it’s about understanding space, structure, measurement, and logical reasoning. With this guide, you now have access to all the geometry basics, formulas, and theorems explained for students.
Keep practicing problems, refer to diagrams, understand real-world applications, and revisit each topic regularly to strengthen your grasp on one of the most scoring sections in mathematics. Remember, visualization makes comprehension easier. So sketch, label, measure, and succeed!
Happy learning and happy proving!
Table of Contents






Get Social