Exploring Quadratic Equations

Quadratic equations are a foundational concept in Class 10 mathematics and beyond. These second-degree algebraic expressions are widely used across science, engineering, economics, and daily life scenarios. Understanding them lays the groundwork for more advanced topics like polynomials, calculus, and real-world modeling. In this extended guide, we’ll explore quadratic equations in depth — including their types, methods of solution, real-life significance, connection with arithmetic progressions (AP), graphical representations, and more.

What is a Quadratic Equation?

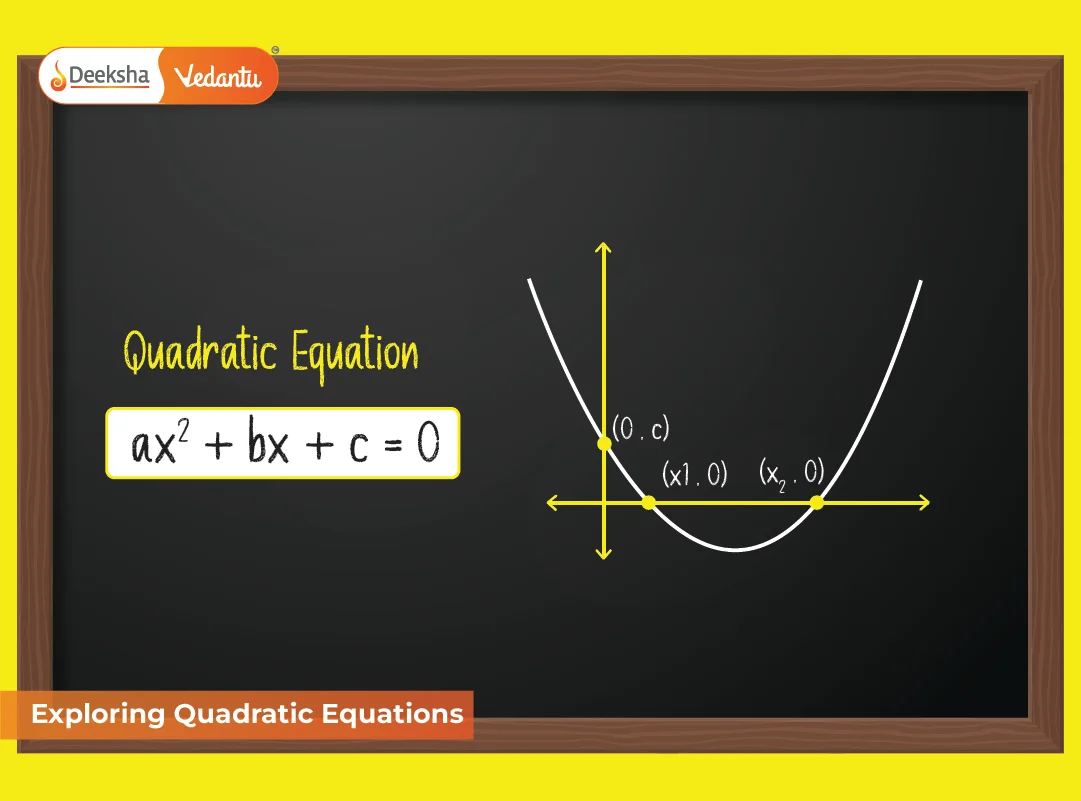
A quadratic equation is a polynomial equation of degree 2 in the form:

ax² + bx + c = 0, where a ≠ 0

Here:

• x is the variable
• a, b, and c are real-number coefficients

This equation represents a parabola when plotted on a graph. The term “quadratic” comes from the Latin word quadratus, meaning “square,” because the highest exponent of the variable is 2.

Quadratic equations are critical in algebra because they represent relationships where a variable is squared — leading to curves instead of straight lines.

🔗 Introduction to Quadratic Equations

Types of Quadratic Equations

Quadratic equations can be categorized based on the presence or absence of certain terms:

• Pure Quadratic Equations: No linear term (b = 0), e.g., 4x² – 36 = 0
• Incomplete Quadratic Equations: Either the linear term (b) or the constant (c) is missing
• Complete Quadratic Equations: All three terms (ax² + bx + c) are present

This classification helps determine the most efficient method for solving the equation.

Standard Form and Important Terms

The general form of a quadratic equation is:

ax² + bx + c = 0

Where:

• a is the coefficient of x²
• b is the coefficient of x
• c is the constant term

Roots or solutions of the quadratic equation are the values of x that satisfy the equation.

Discriminant (D) = b² – 4ac

• If D > 0 → Two distinct real roots
• If D = 0 → Two equal real roots
• If D < 0 → No real roots (complex roots)

Methods of Solving Quadratic Equations

1. Factorisation Method

This method is most efficient when the middle term can be easily split into two values whose product equals ac and whose sum equals b.

Steps:

• Multiply a × c
• Find two numbers that add to b and multiply to ac
• Rewrite the equation by splitting the middle term
• Factorise using common methods

🔗 Solution of a Quadratic Equation by Factorisation

Example:
x² – 7x + 12 = 0 → (x – 3)(x – 4) = 0 → x = 3, 4

2. Completing the Square

Used when factorisation is not straightforward. This method involves rewriting the equation so the left-hand side becomes a perfect square trinomial.

Steps:

• Divide all terms by a (if a ≠ 1)
• Move constant to the right side
• Add the square of half the coefficient of x to both sides
• Factor the perfect square
• Solve by taking square roots

Example:
x² + 8x + 16 = 0 becomes (x + 4)² = 0 → x = –4

3. Quadratic Formula

The universal method for solving any quadratic equation:

x = (-b ± √(b² – 4ac)) / 2a

This method always works regardless of whether the equation is factorable.

Example:
Solve 3x² – 5x – 2 = 0
D = 25, x = (5 ± √25) / 6 = (5 ± 5) / 6 → x = 10/6 = 5/3 or 0

4. Graphical Method

• When plotted, every quadratic equation produces a parabola.
• The x-intercepts of the parabola are the roots of the equation.
• The vertex gives the maximum or minimum value.
• The axis of symmetry is the vertical line through the vertex (x = –b/2a)

Graph features:

• Opens upward if a > 0
• Opens downward if a < 0
• The vertex is a minimum point if a > 0, maximum if a < 0

Visualizing the Graph of a Quadratic Equation

Let’s take the equation x² – 4x + 3 = 0

Factorised: (x – 1)(x – 3) → x = 1 and 3

This means:

• The graph cuts the x-axis at 1 and 3
• The vertex lies midway at x = 2
• The minimum value of the function occurs at x = 2

Graphing such equations helps students understand the symmetry, shape, and roots visually — an essential part of conceptual understanding.

Real-World Applications of Quadratic Equations

Quadratic equations are used in numerous real-life situations:

• Physics: Calculating projectile motion, velocity under gravity
• Economics: Revenue and profit maximization problems
• Engineering: Designing parabolic structures like bridges and antennas
• Biology: Modeling population growth curves
• Business: Predicting product sales or losses
• Agriculture: Calculating optimum area for enclosed fields

Understanding quadratic equations enables learners to apply math to meaningful and complex real-world problems.

Connection to Arithmetic Progressions (AP)

Quadratic equations are often used in solving problems involving Arithmetic Progressions.

Example:

The nth term of an AP is:
Tₙ = a + (n – 1)d

Suppose Tₙ = 0. Then:
a + (n – 1)d = 0 → Solve for n → results in a quadratic equation in terms of n.

🔗 Introduction to Arithmetic Progressions
🔗 Nth Term of an AP
🔗 Sum of First n Terms of an AP

AP problems involving series, sums, or positions of terms often require quadratic equations for resolution.

Sample Problems

Q1: Solve x² + 7x + 10 = 0 using factorisation.
Ans: x = –2, –5

Q2: Solve 3x² + 2x – 1 = 0 using the quadratic formula.
Ans: x = 1/3, –1

Q3: What is the nature of roots of x² + 4x + 5 = 0?
Ans: Discriminant = –4 → No real roots (complex roots)

Q4: Find the value of k for which x² + 2x + k = 0 has equal roots.
Ans: Set D = 0 → (2)² – 4 × 1 × k = 0 → 4 – 4k = 0 → k = 1

FAQs

Q1. What is the quadratic formula used for?
It’s used to find the roots of any quadratic equation where a, b, and c are known.

Q2. Why does the graph of a quadratic equation form a parabola?
Because the equation includes a squared term (x²), it curves and forms a parabola.

Q3. How do I know which method to use to solve a quadratic equation?
Try factorisation first. If it’s not possible, use the quadratic formula or completing the square.

Q4. Is graphing a necessary part of understanding quadratics?
Yes. Visualising the graph gives a deeper conceptual grasp of roots, vertex, and symmetry.

Q5. Are quadratic equations part of the Class 10 CBSE board exam?
Absolutely. They are one of the most important topics and carry high weightage.

Q6. What happens if the discriminant is negative?
The quadratic equation will have no real roots, only complex ones.

Conclusion

Quadratic equations offer a powerful tool to decode the world through mathematics. By mastering the various solution techniques, understanding their geometric representation, and recognizing their role in real-life scenarios, students not only prepare for exams but also sharpen analytical thinking.

Practice solving a variety of problems, visualize graphs, and relate equations to real-life scenarios to truly excel in this essential Class 10 math topic. Stay connected for more in-depth guides and worksheets from Deeksha!