,
, and
, we can determine the type of solution:
, the lines intersect and there is a unique solution.
, the lines are coincident and there are infinitely many solutions.
, the lines are parallel and there is no solution.

 , the lines intersect and there is a unique solution.
, the lines intersect and there is a unique solution.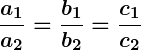 , the lines are coincident and there are infinitely many solutions.
, the lines are coincident and there are infinitely many solutions.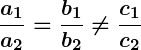 , the lines are parallel and there is no solution.
, the lines are parallel and there is no solution.

Get Social