Some Applications of Trigonometry Class 10 Notes

In this post, some applications of trigonometry class 10 notes are covered. You’ll learn everything about trigonometry’s applications in various fields.Trigonometry is a vital field or subset of Mathematics. Without addressing this topic, the learning of this subject is insufficient, which is why it is also covered in Class 10 board examinations. As we all know, the Class 10 Board is a significant stage for any student, and all students want to get excellent grades in the board examinations. To complete the entire syllabus of this subject, we need revision notes at the end, so we are here to assist the students with the trigonometry revision notes that will assist them in their preparation and final exams as well.

In this article, we have provided some applications of trigonometry class 10 notes, which is one of the most significant and scoring chapters of Class 10. To cover this crucial chapter, you will need revision notes, and these notes will address your difficulties.

Applications of Trigonometry

Trigonometry has the following practical applications:

• It assists in determining the separation/distance between celestial bodies: The parallax technique can be used to measure long distances. When an item is observed from two perspectives, the parallax angle is half the angle between the two lines of sight. If we know the angle of the parallax and the distance between the places, we can use trigonometry to calculate the distance.
• It is used for gauging length while building structures and towns: Only trigonometry is used to determine the size of a structure to be built or planned.
• It is useful for calculating heights and distances.
• It is used in oceanography to calculate the height of tidal waves.
• The sine and cosine functions are commonly employed to calculate sound and light waves.
• Calculus has trigonometry and algebra.
• It benefits cartography or the making of maps.
• Trigonometry is in computer music in the form of sound waves.
• It is useful for determining the length of mountains, rivers, and other bodies of water.
• It is utilised in satellite communication systems.

Trigonometry’s Applications in Various Industries

The following are the applications of trigonometry in various industries:

Trigonometry in Aviation

• Trigonometry is used in the aviation industry to determine the direction, distance, and speed of the wind as well as the plane.
• The wind direction is critical in this field for pilots to fly a plane.

Trigonometry in Criminology

• When a crime scene has to be investigated, trigonometry is used.
• Trigonometric ratios can also be used to calculate the trajectory or route of the bullet.
• It is also used to calculate the phenomena of a falling item with a specific angle.

Trigonometry in Marine Biology

• Marine scientists commonly use trigonometry to determine the depth of sunlight impacting algae growth for photosynthesis.
• They attempt to assess the size of other species as sharks and whales and monitor their behaviour so that algae are not affected.

Trigonometry in Navigation

• It is used for calculating and navigating directions to acquire a straight direction by placing the compass.
• It is easy to pinpoint the distance to view the horizon using a compass and trigonometric functions.

Trigonometry in Video Games

• Rather than leaping straight along the y-axis, a character in many games, such as Mario, glides across the surface in a parabolic/curved route, guarding the blocks/hurdles in its path.
• Mario can overcome these challenges thanks to trigonometry. Trigonometry is also a crucial factor for these game developers.

Trigonometry in Construction

• We require trigonometry. In construction, for assessing fields, lots, and regions; making structures parallel and perpendicular; laying ceramic tiles; estimating roof inclination; determining building height, length, breadth and so on.

Trigonometry in Marine Engineering

• Trigonometry is used in maritime engineering to design and navigate ships.
• Trigonometry is utilised in constructing maritime ramps that connect higher and lower levels via a sloping surface/staircase based on the necessity and application.

Trigonometry in Physics

• Trigonometry is used to calculate angles. It is used to discover dot and cross products and other vector components.
• It is also used to study electromagnetic waves and the processes of wave and oscillation models.
• We also utilise trigonometry to calculate and determine projectile velocity.

Trigonometry for Archaeologists 

• Archaeologists use trigonometry to divide the dig site into equal portions while retaining symmetry.
• They must identify several tools for their task. Archaeologists also measure the subsurface water and tank systems.

Angles of Elevation and Depression

A line of sight is a straight line traced from an observer’s eye to a point in the object being seen.

The Angle of Elevation

The intersection of the horizontal line and the line of sight obtains the angle of elevation. If the line of sight is directed upward from the horizontal line, the resulting angle is an angle of elevation.

As shown in the image below, an observer is gazing at the object while standing on the ground, producing an angle between the line of sight and the horizontal line. A right-angle triangle is constructed by connecting an imaginary line between the object and the end of the horizontal line. Thus, we may use trigonometry to calculate the distance between the observer and the tower or structure. The height of the tower or structure, or the height at which the object is held, is called perpendicular, and the horizontal line is considered the opposite side of the triangle created. 

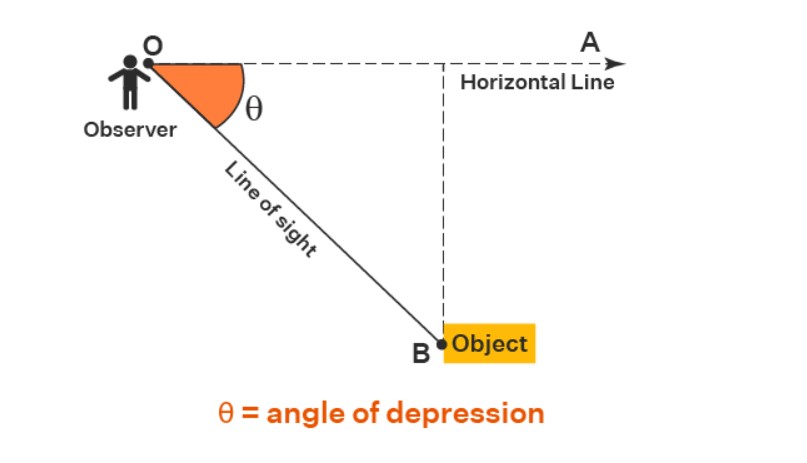
The Angle of Depression

The angle of depression is the angle formed by the horizontal line and the object as seen from the horizontal line. It calculates the distance between two objects where the angles and distance from the ground are known. If the line of sight is downwards from the horizontal line, it forms an angle with the horizontal line.

If the object being seen is below the observer’s level, the angle obtained between the horizontal line and the observer’s line of sight is known as the angle of depression. In the diagram below, θ is the angle of depression.

Calculating Heights and Distances

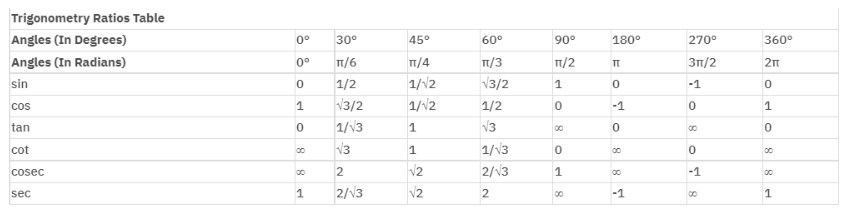
We can employ trigonometric ratios to compute heights and distances.

For reference, check out the trigonometric ratio table below:

Step 1: Create a line diagram corresponding to the situation.

Step 2: Label all known heights, distances, and angles, and use variables to signify unknown lengths.

Step 3: Using the values of various trigonometric ratios of the angles, calculate the undetermined lengths from the known lengths.

Heights and Distance Summary

The figure below summarises height and distance completely.

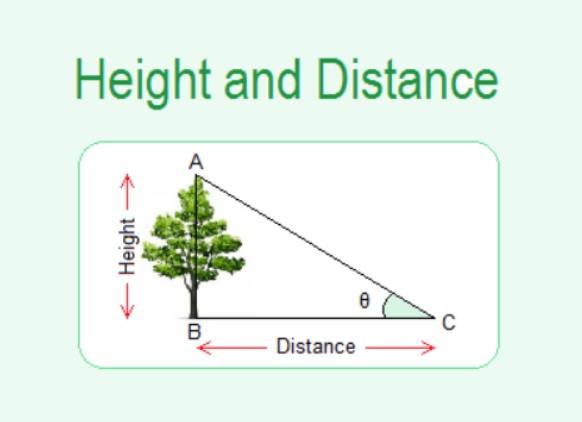
If C is the point of observation, then:

• AC is the line of sight, according to the illustration
• BC is the distance between the witness and the object
• AB denotes the object’s height
• α is the angle of elevation
• β is the angle of depression

Using Trigonometry to Calculate the Distances Between Celestial Bodies

The parallax technique is useful for measuring long distances. When an item is observed from two separate perspectives, the parallax angle is half the angle between two lines of sight. Large distances can be measured using the parallax angle and the distance between the two places.

Benefits of Some Applications of Trigonometry Class 10 Notes

• Some Applications of Trigonometry Class 10 Notes are created in such a manner that students can go over all of the topics at once in a short amount of time without missing any crucial chapter concepts.
• Revision notes for Chapter 9 will help students in a variety of ways, including speeding up their problem-solving abilities, which we propose students practise and revise regularly.
• Notes for Class 10 Revision Some Trigonometry Applications will assist you in covering the major and scoring subjects of the syllabus is Trigonometry, and Chapter 9 is regarded as one of the trickiest and scoring chapters, and these notes will assist you in preparing this topic.
• Some Applications of Trigonometry Class 10 Notes are prepared and presented in a most visual and detailed manner. We kept every crucial factor in mind when writing these notes, such as your exam pattern, important ideas that need to be underlined, all topics relevant to Chapter 9 and Trigonometry and more.
• Students can learn and revise formulas or concepts just before the exam with Math’s applications of trigonometry class 10 notes and this revision will accelerate the exam preparation and help them in solving long statement-based questions.
• Notes of Class 10 review Notes Chapter 9 will be advantageous if students have the practice of revising these notes before beginning problem-solving. Experts create the revision notes with the student’s need for last-minute revision in mind so that they can boost their performance.
• Preparing notes for review at the end in such a manner that you take less time studying each chapter is time-consuming but vital, and these Class 10 Maths Revision Notes Chapter 9 will help you save that time, which you can then use to practice, which is more crucial for mastering the concepts.

General Tips

• As it is one of the most difficult chapters in Class 10, read through every topic and idea in Ch 9 Class 10 Math’s review notes when revising.
• Preferably, revise it before beginning to solve the problems in the chapters. This chapter deals with statement-based questions and drawing their diagrams; only then will you be able to answer the question at the conclusion.
• Revise the notes from Chapter 8 on Introduction to Trigonometry, as some of the fundamental principles from that chapter will be used in Chapter 9.
• Before beginning the Trigonometry chapter in higher classes, you can go through it again.

Conclusion

Trigonometry is the crucial scoring topic. It consists of two chapters in particular, and questions on this topic are asked every year. For this reason, Class 10 Maths applications of trigonometry class 10 notes can assist you in this crucial topic so that you can quickly complete last-minute revisions without missing any points.

These notes are designed for students who are studying for their board exams and want to do well in them by being in line with the syllabus and requirements for Class 10 Board examinations. Some applications of trigonometry class 10 notes have saved you a tremendous amount of time by presenting these notes, so all you have to do now is concentrate on your study and preparation to do well. All the best for your class 10 Maths exams!

FAQs

Define “line of sight.”

A right-angled triangle is produced by the intersecting lines of your body as you stand, the horizontal line, and the line connecting the observer’s eyes to the item. The line of sight is the term for the right-angled triangle’s hypotenuse.

 Are all of the exercises necessary for Chapter 9 some applications of trigonometry class 10 Math Class 10?

Yes, all of the exercises in NCERT Class 10 Math Chapter 09, Some Applications of Trigonometry, are crucial in terms of exams. You can always rely on the NCERT Solution for Class 10 Maths if you are having trouble with the exercises to come up with the right step-by-step solution. 

How can the NCERT solution for Chapter 9, some applications of trigonometry class 10 of Class 10, be useful in the examination?

All of the problems from the NCERT book’s solutions are provided here by subject-matter experts, and they are based on the most recent and updated curriculum and CBSE 2022–2023 criteria. Using these solutions, you can boost your drive to do well in Class 10, 2023 examinations.