Circles Class 10 Notes

CBSE Class 10 Circle Notes contain concept-by-concept explanations for all the terms. These notes were created by experts and adhere to CBSE guidelines.The CBSE Class 10 circles notes are carefully written to assist students in understanding the concepts, topics, and concerns presented in the Circles chapter. The Circle chapter revision notes are based on the most recent curriculum the CBSE has approved. These helpful notes relieve students of the burden of purchasing several books to study for the exam time. The emphasis on important topics and using concrete examples to clarify concepts in the circles class 10 Notes push pupils to do well on examinations. Get the whole set of class 10 notes for the chapter on the circle as a downloadable pdf. These notes are beneficial for students preparing for the CBSE board exams in 2022–2023.

Below, we have included a brief overview of the CBSE Notes of Class 10, which provide an excessive application of all the major themes of the circle chapter.

Overview of CBSE Class 10 Circle Revision Notes

Class 10 Circles notes discuss the presence of tangents in a circle as well as some of the features of a circle. Tangents, tangents to a circle, and the number of tangents from a point on the circle are presented to students.

Students can learn the topics associated with circles by using the circle notes as a reference. They will also benefit from our solution’s ability to help them perform well on the test.
Circle notes Answer all of the practice questions from the NCERT Maths Class 10 textbook. The comprehension of students for the subjects is improved by practising challenging questions.
In addition to learning about significant subjects in the chapters, students may efficiently get ready for tests. By obtaining the circle Notes for Class 10 PDF, students may quickly understand the circle chapter’s concepts, theorems, and methods.
Subject matter experts in the circle carefully crafted these review notes for Class 10 circle students. The notes clearly and completely offer study material for each chapter.
Experts have covered each subject in-depth to guarantee that students fully comprehend the material.
With the help of these notes, students will be able to gain an understanding of the chapters, making them excellent study tools.
The circle Class 10 Notes’ major benefit is that it emphasises key concepts and provides examples to explain diagrams, which encourages students to perform well on tests.
The circle chapters for Class 10 include a lot of material that students may only fully understand after going over the chapters once again. The Class 10 notes are useful in this situation.
Circle notes for grade 10 Discuss the revised CBSE Syllabus and the kinds of questions that could be posed during the test. Students will benefit from practising significant drawings. The circle notes are also useful for remembering crucial calculations and formulas.
Every significant issue covered in this chapter will be made transparent by the Circles Class 10 Notes, which knowledgeable teachers have created. Additionally, students may utilise these notes to review the material thoroughly before the exam without skipping any crucial points, practice problems, and have a full revision of the chapter.

CBSE Class 10 Chapter Circle Notes

The Explanation about circles, tangents to circles, the Number of tangents from a point on a circle, and a summary of the entire chapter are the topics covered in the NCERT book for the class 10 Circle chapter. This chapter focuses on tangents to circles and the number of tangents at various places on a circle. We frequently see circles in our daily lives. Complex terms like tangents, tangents to a circle, and the number of tangents from a certain point on the circle are introduced to the students. Due to the illustrations, the use of geometric calculations, the existence of tangents to circles, and several other characteristics of circles, this chapter appears to be quite interesting.

Revision Notes of Circle Class 10

Meaning of Circle: Since all points on a circle’s surface are equally spaced from the point known as the “centre,” we know that a circle is a closed, two-dimensional geometric shape. Radius is the measurement of a circle’s distance from any point on its surface to its centre.
Circle and line in a plane: There are three possible permutations for a circle and a line on a plane.

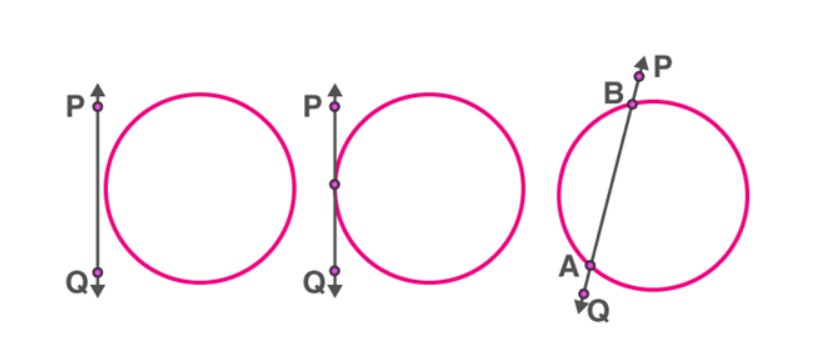
(i). They may not intersect.

(ii). In this instance, the line hits the circle, demonstrating how they can share a single point.

(iii). In this instance, the line cuts the circle, indicating they can share two points.

Tangent to a circle: A tangent to a circle is a straight line that only makes one contact with the circle. This area is known as the point of tangency. The tangent to a circle is parallel to the radius at the point of tangency.
Two or more lines that do not intersect make up a non-intersecting line. The circle and the line AB in fig. I do not have a common point. Noteworthy facts include:

i). Lines that never intersect will never meet.

ii). Another name for them is parallel lines.

iii). They keep the same spacing between them at all times.

Secant to a Circle: A secant is a line intersecting curves at two or more points. In the case of a circle, a secant crosses it at precisely two points.

The line AB meets the circle at two locations, A and B, in the below figure. The circle’s secant is AB.

Tangent as a special case of Secant: When the two ends of its corresponding chord coincide, the tangent to a circle can be thought of as a specific instance of the secant.

A particular secant can only have two parallel tangents: There are precisely two tangents parallel to and touching the circle at two diametrically opposing locations for every given secant of a circle.

We can see the following points from the diagram:

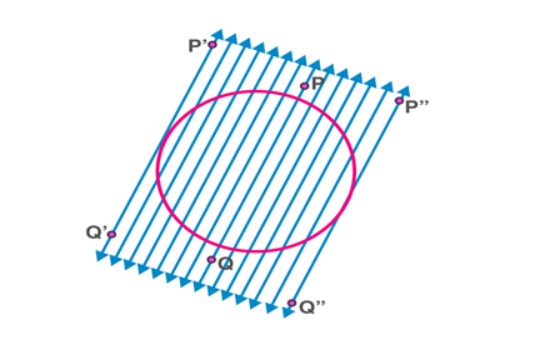
i.PQ is the circle’s secant.

Ii. P’Q’ and P”Q” are two parallel tangents to PQ.

Properties of Tangents drawn to a circle:

i.Only a tangent can be present at one point of contact in a circle.

Ii. No point outside the circle may be used to create a tangent.

Iii. There are only two tangents that exist from any point outside the circle.

Iv. Theorems demonstrating the characteristics of a circle’s tangent

Theorem 1: “The tangent to the circle at any point equals the perpendicular to the radius of the circle that passes through the point of contact.”

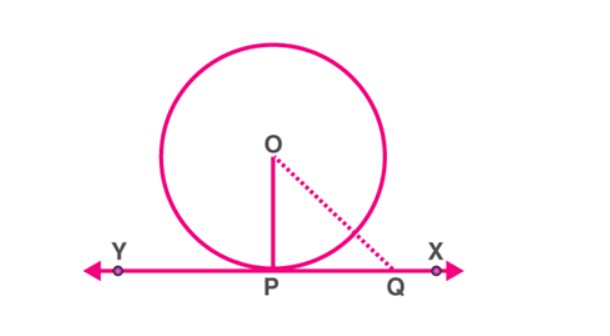
Theorem Proof: Consider a circle with point “P” as the centre and XY as the circle’s tangent at “O.” We must now demonstrate that OP is parallel to the tangent XY.

Now think about a point Q that is not P on the tangent line XY. As illustrated in the diagram, connect the points OQ.

Point Q should be outside the circle in this instance. Because XY will not be a tangent to the circle if point Q is within the circle, It denotes that XY will eventually become a circle’s secant.

OQ should thus be larger than OP’s radius.

It implies that.

OQ > OP

Given that all locations on line XY except P comply with this criteria, OP should be the shortest distance between the centre of circle “O” and the points on line XY.

As a result, we may say that OP is parallel to XY.

The theorem is so proof.

Theorem 2: Tangents formed from an outside point to a circle have identical lengths.

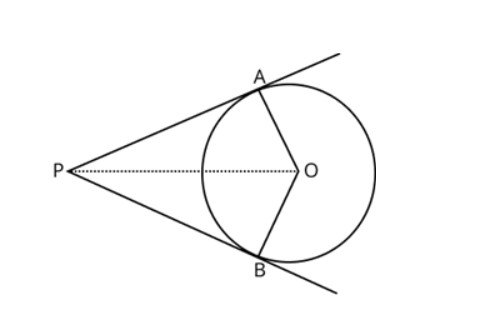
Theorem Proof: Assume we are given a circle with “O” at its centre and “P” as the point outside the circle

According to the diagram, the two tangents that are created here are PQ and PR on the circle starting at point P.

We must now demonstrate that PQ Equals PR.

We now need to combine OP, OQ, and OR to demonstrate this.

The angles created between the tangents and radii are right angles according to the axiom “The tangent to the circle at any point is the perpendicular to the radius of the circle that passes through the point of contact.”

As a result, two right angles, such as QOP and ORP, are created.

Thus, we may write OQ = OR using the radii of the same circle.

The common side is OP = OP.

Consequently, applying the RHS congruence rule, QOP ≅ ORP

PQ = PR is therefore obtained using CPCT.

So, the theorem is proved.

Theorem 3: It claims that the lengths of the tangents drawn from an outside point to a circle are equal.

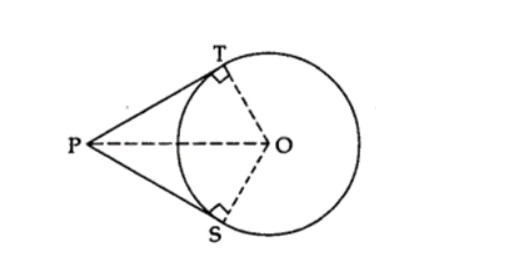
Theorem Proof: In ∆OTP and ∆OSP.

OT = OS …[radii of the same circle]

OP = OP …[common]

∠OTP = ∠OSP …[each 90°]

∆OTP = ∆OSP …[R.H.S.]

PT = PS …[c.p.c.t.]

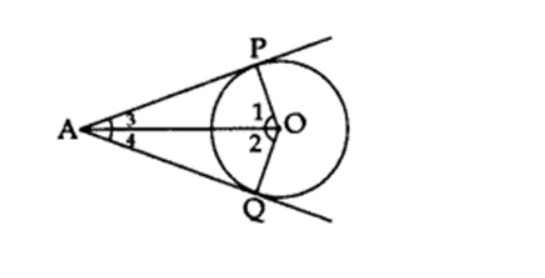
Note: If two tangents are drawn from an outside point to a circle, then:

At the center, they subtend identical angles that are ∠1 = ∠2.

They both lean in the same direction toward the segment connecting the center to that point, i.e., ∠3 = ∠4., and ∠OAP = ∠OAQ

General Terminology of Circle Chapter

Circle: It is described as gathering every point in a specified plane positioned at a given distance from another point.
Centre: The centre is a fixed location from which every other point is equally distant.
Radius: The term “radius” refers to the constant distance from the centre at which all other points are equally spaced.
Chord: The line segment that connects two points on a circle is referred to as a chord.
Diameter: The diameter of a circle is the length of the chord that runs through its center. This chord is the longest.
Tangent: when a line crosses a circle at one or more coincident points A tangent is the name given to the line.
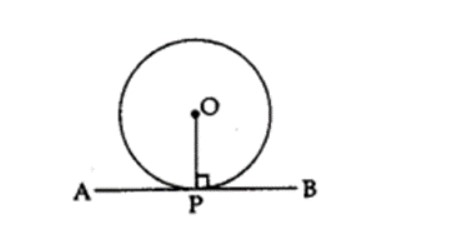
The radius via the point of contact is perpendicular to the tangent to a circle.

OP ⊥ AB

Two tangents from an outside point to a circle have equal lengths.

AP=PB

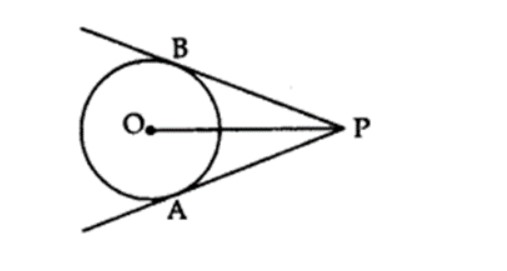
Tangent Segment Length

Normal terminology refers to PB and PA as the lengths of tangents from outside point P.

Properties and Facts of Circle

The bigger circle’s chord, which hits the smaller circle, is split at the point of contact in two concentric circles.
The tangents drawn at the circumference of a circle’s diameter are parallel.
The centre of a circle is traversed by the perpendicular at the point of contact with the tangent.
The angle subtended by the line segment connecting the points of contact at the centre is in addition to the angle formed by the two tangents drawn from an outside point to the circle.
A rhombus is the shape of a parallelogram that surrounds a circle.
A quadrilateral around a circle has opposing sides that subtend additional angles at the circle’s centre.

Solved Examples of Circle chapter

Example 1: In the given figure, PA and PB are tangents to the circle with centre O. If ∠APB = 60°, then calculate ∠OAB.

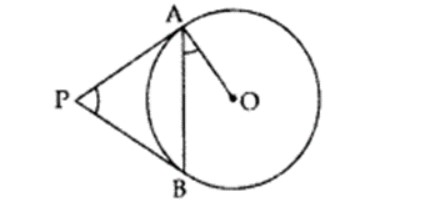
Solution:

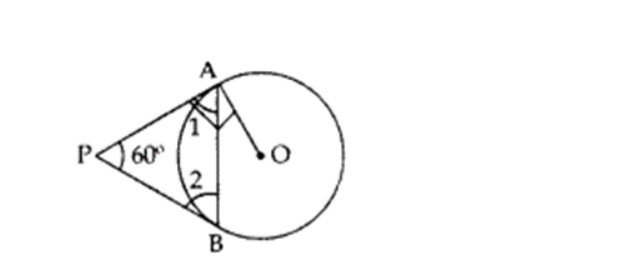
∠1 = ∠2

∠1 ∠2 ∠APB = 180°

∠1 ∠1 60° = 180°

2∠1 = 180° – 60° = 120°

∠1 = 120∘2 = 60°

∠1 ∠OAB = 90°

60° ∠OAB = 90°

∠OAB = 90° – 60° = 30°

Example 2: Show that the tangents drawn at the circle’s endpoints are parallel.

Solution: A circle with an O-centered centre and an AB diameter should exist. The tangents to the circle at A and B are CD and EF, respectively.

We will demonstrate that CD || EF

Therefore, OA CD and OB EF.

At the point of contact, the circle’s radius is perpendicular to the tangent.

Consequently, the alternative interior angles between CD and EF are equal (is of 90o).

⇒ CD || EF Lines are parallel if the opposing angles are equal.

Practice Questions as per CBSE Curriculum

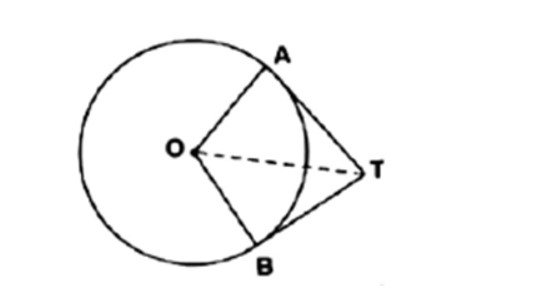
Q1) In the figure, if ∠ATO = 40°, find ∠AOB.

Q2) The two tangents from an external point P to a circle with centre O are PA and PB. If ∠APB = 70°, then what is the value of ∠AOB?

Q3) In two concentric circles, a chord of the larger circle touches the smaller circle. If the length of this chord is 8 cm and the diameter of the smaller circle is 6 cm, then find the diameter of the larger circle.

Q4) Let there be a point P exterior to the circle with the centre at O such that OP = 10cm. If PT is a tangent to the circle of length 8 cm. Find the radius of the circle.

Q5) From a point P outside a circle with centre O, tangents PA and PB are drawn to the circle. Prove that OP is the right bisector of segment AB.

Benefits of Revising 10th Circle Notes

The following are some of the most significant advantages of CBSE class 10 circle notes:

In keeping with the saying that “practice makes a man perfect,” we have created these Circles Class 10 Notes in pdf format to assist you in identifying your preferred methods of learning.
You may use the PDF of these Circles Class 10 notes to study and do well on your exams. Circles Notes are available for download by merely clicking once on the pdf link provided below, which will assist most students in getting ready for this topic and performing well on their math examinations. To learn everything there is to know about circles, download the PDF.
The students can prepare for exams by using these revision notes. It helps students understand ideas more quickly and dispels their uncertainties.
Before tests, the revision notes will help pupils recall more information about the circle chapter. Because of the clear and simple language used in the circle chapter, students may quickly remember the theorems, formulae, and procedures discussed there.
In the CBSE Class 10 Maths curriculum, the chapter on circles is one of the most fascinating and often studied. In order for students taking the class 10 test to be completely prepared with all the key knowledge they may need to achieve high marks, our skilled teachers must supply them with all the study materials and necessary notes. For last-minute revision, we suggest students read over these revision notes.
All of the crucial circle-related concepts are covered in the Class 10 Maths Chapter circle Notes. Our professionals have carefully compiled these notes to aid students in their studies and academic performance. The students may use the provided PDF to their advantage and study whenever they choose. Additionally, appropriate examples are used to cover each of these subjects.
Students may learn how to respond to both subjective and objective questions with the help of these NCERT class 10 circle notes.
The notes help students resolve any questions they may have regarding a certain chapter. Students can use the revision notes to guide them through challenging subjects.