Coordinate geometry, also known as Cartesian geometry, is a powerful mathematical tool that bridges algebra and geometry by using graphs and coordinates. It provides a systematic method to study and analyze geometric figures using numbers and equations. By placing figures on a coordinate plane, you can solve complex geometry problems with ease.
Whether you’re calculating the distance between two points, finding the midpoint of a segment, or determining how a line is divided in a specific ratio, coordinate geometry helps you approach these problems in a logical and visual way. It is a fundamental part of Class 10 mathematics and plays a significant role in board exam preparation and higher-level math studies.
This comprehensive guide will help you explore the foundational principles, geometry formulas for Class 10, real-life applications, and related concepts that enhance your understanding of this important topic.
Start with Introduction to Coordinate Geometry
Understanding the Coordinate Plane
The coordinate plane is made up of two perpendicular number lines: the horizontal x-axis and the vertical y-axis. They intersect at the origin (0, 0). Any point on this plane is represented by an ordered pair (x, y), where ‘x’ denotes the horizontal position and ‘y’ denotes the vertical position.
Four Quadrants
The coordinate plane is divided into four quadrants:
- Quadrant I: Both x and y are positive (+x, +y)
- Quadrant II: x is negative, y is positive (–x, +y)
- Quadrant III: Both x and y are negative (–x, –y)
- Quadrant IV: x is positive, y is negative (+x, –y)
Understanding which quadrant a point lies in helps with graphing, analyzing shapes, and solving geometry-based problems more efficiently.
Key Coordinate Geometry Formulas for Class 10
Memorizing the basic formulas in coordinate geometry is essential for solving problems quickly and accurately. Here are the three most important ones:
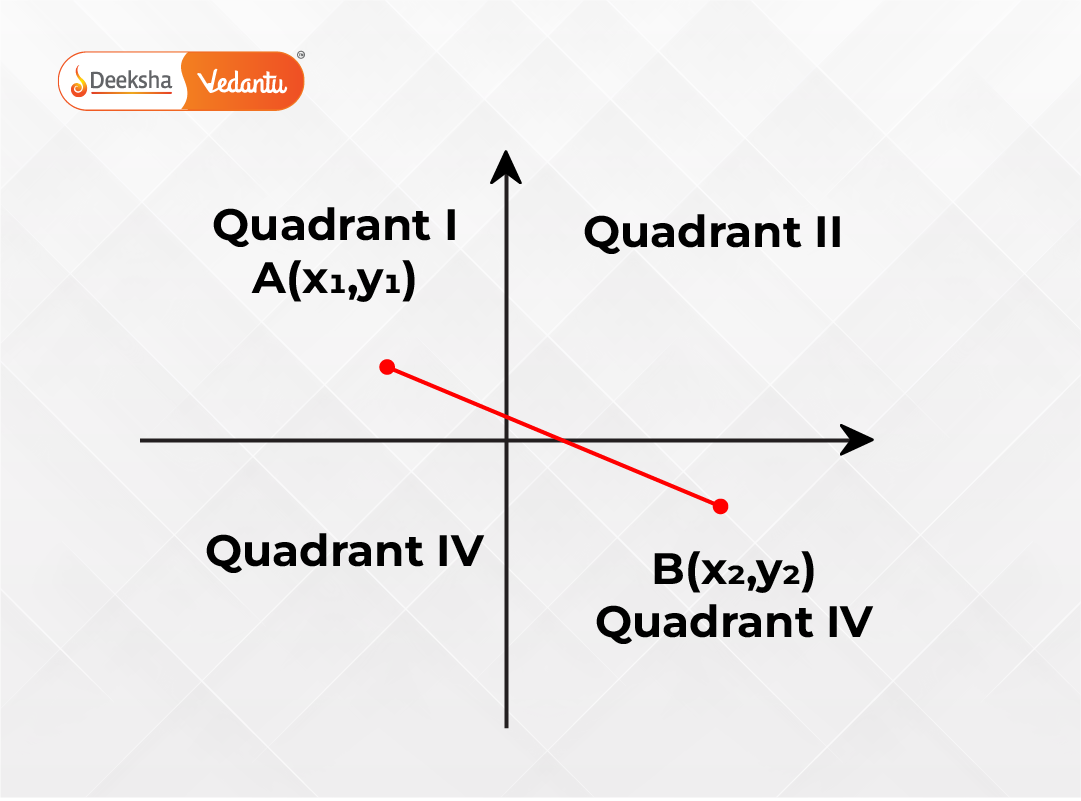
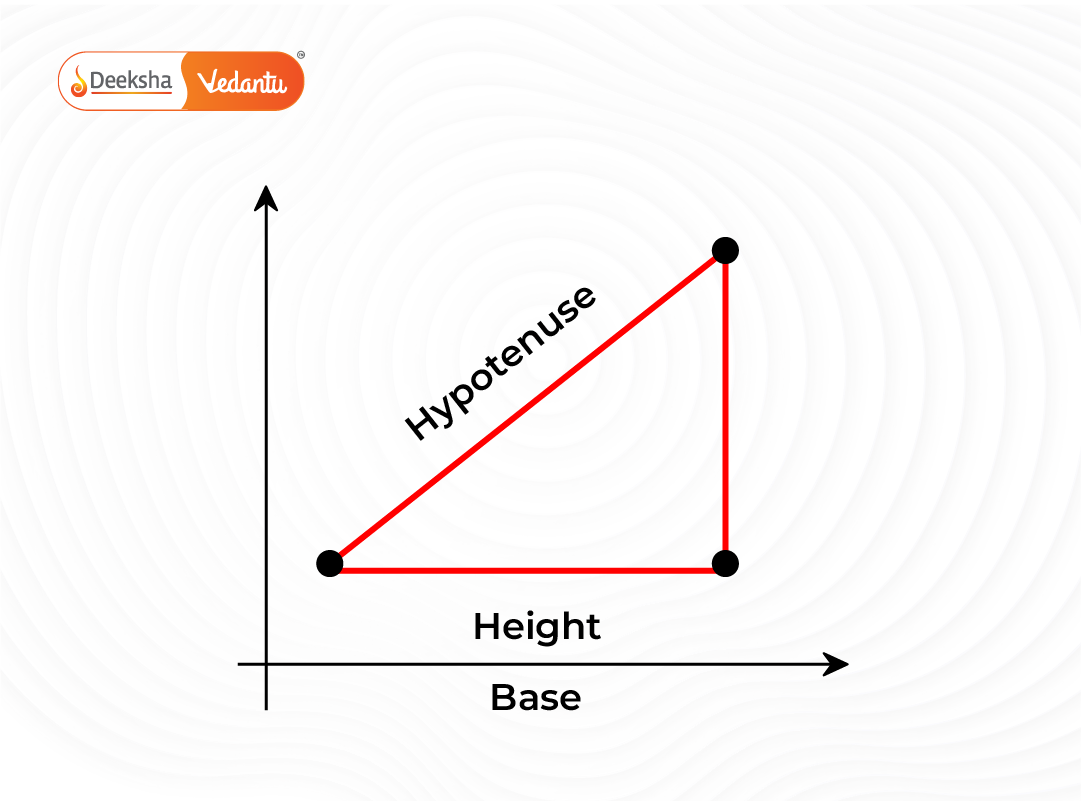
1. Distance Formula
The distance between two points and
on the coordinate plane is calculated using:
This formula is based on the Pythagorean theorem and is used to find the length of a line segment joining two points.
Explore: Coordinate Geometry Distance Formula
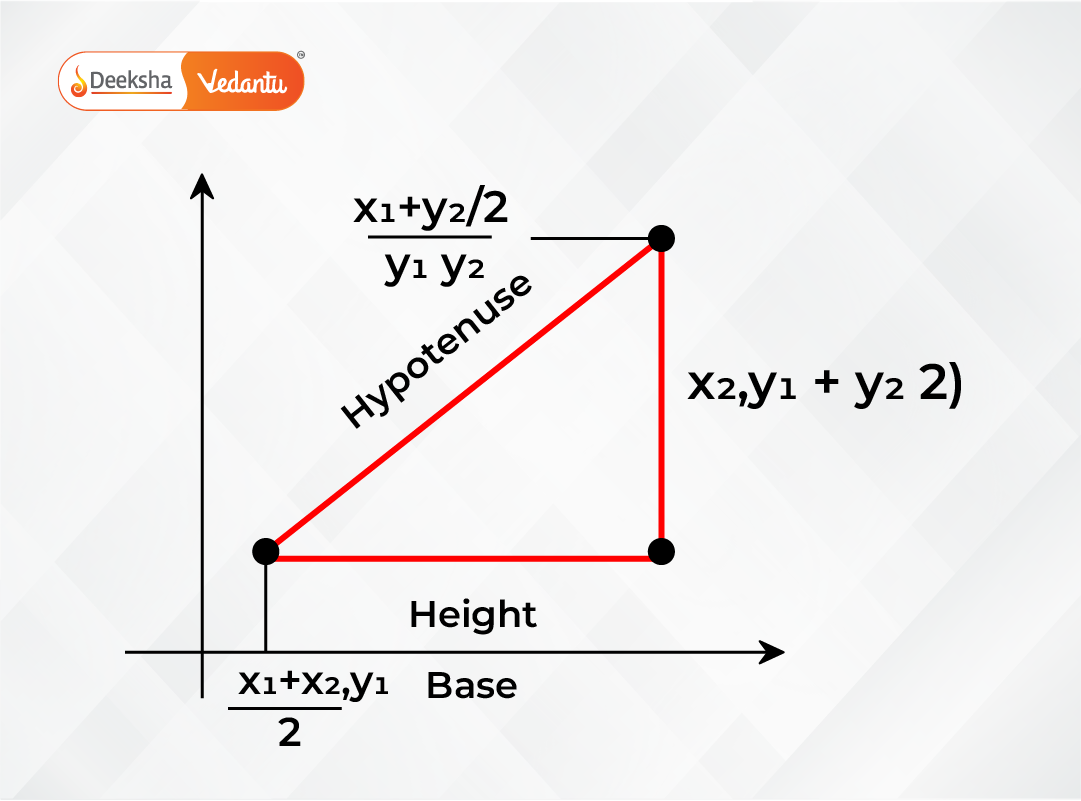
2. Section Formula
When a point P divides the line segment joining points A and B
in the ratio m:n, the coordinates of P are given by:
This formula is widely used to find coordinates of a specific point on a line segment, whether it lies internally or externally.
Explore: Coordinate Geometry Section Formula
3. Midpoint Formula
The midpoint M of a segment joining A and B
is:
This is a specific case of the section formula where the ratio is 1:1. It’s frequently used in problems requiring symmetry.
Real-World Applications of Coordinate Geometry
Coordinate geometry is not just a chapter in your textbook—it has many practical uses in daily life and advanced fields. Here are some common applications:
- GPS and Navigation: To find the shortest distance or track movement between two locations
- Engineering and Architecture: Helps design bridges, skyscrapers, and roads with precise alignment
- Astronomy: Used for plotting positions of celestial bodies
- Computer Graphics: Key in animations, video games, and design software
- Robotics and AI: Used to determine location and path planning
Understanding these real-world applications makes learning coordinate geometry more meaningful and engaging.
Related Geometric Concepts
Coordinate geometry provides the foundation for more complex geometric topics that are essential in Class 10 and beyond.
Triangles in Coordinate Geometry
To calculate the area of a triangle formed by three points A, B, and C on a coordinate plane, use:
This formula is especially helpful in problems involving irregular triangles.
Congruence and Similarity of Triangles
Analyzing the properties of triangles in a coordinate setting helps prove:
- Congruency: Using SSS, SAS, and ASA rules
- Similarity: Based on AA, SSS, and SAS similarity criteria
Understanding these relationships is crucial for proving geometric theorems and solving triangle-based problems in coordinate geometry. Applying these properties can simplify complex coordinate-based problems and make them more visual and logical.
Review: Congruence of Triangles
These concepts of congruence are foundational in verifying that two triangles are exactly the same in size and shape, which is a frequent requirement in geometry proofs.
Understand: Similarity of Triangles
Studying the similarity of triangles helps us determine how shapes relate in proportion, even if their sizes differ. This is especially helpful when working with scaled diagrams or maps.
Learn: Criteria for Similarity
Circles in Coordinate Geometry
Circles are represented using the equation: Here, (a, b) is the center and r is the radius.
This equation allows you to identify points on the circle, draw tangents, and more.
Start with Introduction to Circles
Understanding the standard form of a circle’s equation gives you insight into its geometric structure. You can see how shifting the values of a and b changes the circle’s position on the graph, while r alters its size. This concept is especially useful when working with graphical analysis and transformations in math.
Circles in Coordinate Geometry
Circles are represented using the equation:
Here, (a, b) is the center and r is the radius.
This equation allows you to identify points on the circle, draw tangents, and more.
Start with Introduction to Circles
Once you’re familiar with how a circle is represented on the coordinate plane, it’s helpful to explore how lines can interact with circles—especially tangents. Tangents are straight lines that touch the circle at exactly one point, and they have unique properties that are frequently tested in exams.
FAQs on Coordinate Geometry
1. What is coordinate geometry?
Coordinate geometry combines algebra and geometry to solve problems using coordinates on a plane.
2. What is the distance formula used for?
It is used to measure the shortest distance between two points on the coordinate plane.
3. What does the section formula help with?
It determines the exact point dividing a line segment in a given ratio, internally or externally.
4. How is the midpoint formula different from the section formula?
The midpoint formula is a specific case of the section formula when the dividing ratio is 1:1.
5. Is coordinate geometry important for Class 10 exams?
Absolutely. It’s not only important for board exams but also for entrance tests like NTSE, Olympiads, and higher studies in science and engineering.
Conclusion
Coordinate geometry is a cornerstone of mathematical learning in Class 10. By mastering the distance formula, section formula, and midpoint formula, students develop a deeper understanding of how algebra meets geometry in real-world problem-solving.
From plotting points to analyzing shapes and distances, this branch of math empowers you with the tools needed for academic success and practical application. Keep practicing with coordinate-based problems, explore visual aids, and refer to helpful online platforms like Deeksha Learning to reinforce your concepts.
With dedication and curiosity, coordinate geometry can not only boost your exam performance but also your appreciation for how mathematics shapes the world around us.
Table of Contents













Get Social