9.4 Distance of a Point from a Line – Class 11 Mathematics

Introduction

In coordinate geometry, we often need to calculate how far a given point is from a given line. This is not the straight-line distance between arbitrary point and arbitrary point on the line, but the shortest distance, which is always along the perpendicular dropped from the point to the line.

This idea is extremely useful in:

• Checking whether a point lies on a line (distance = 0).
• Finding shortest path problems in physics and optimization.
• Determining equations of loci in competitive exams.
• JEE problems involving distance constraints in geometry.

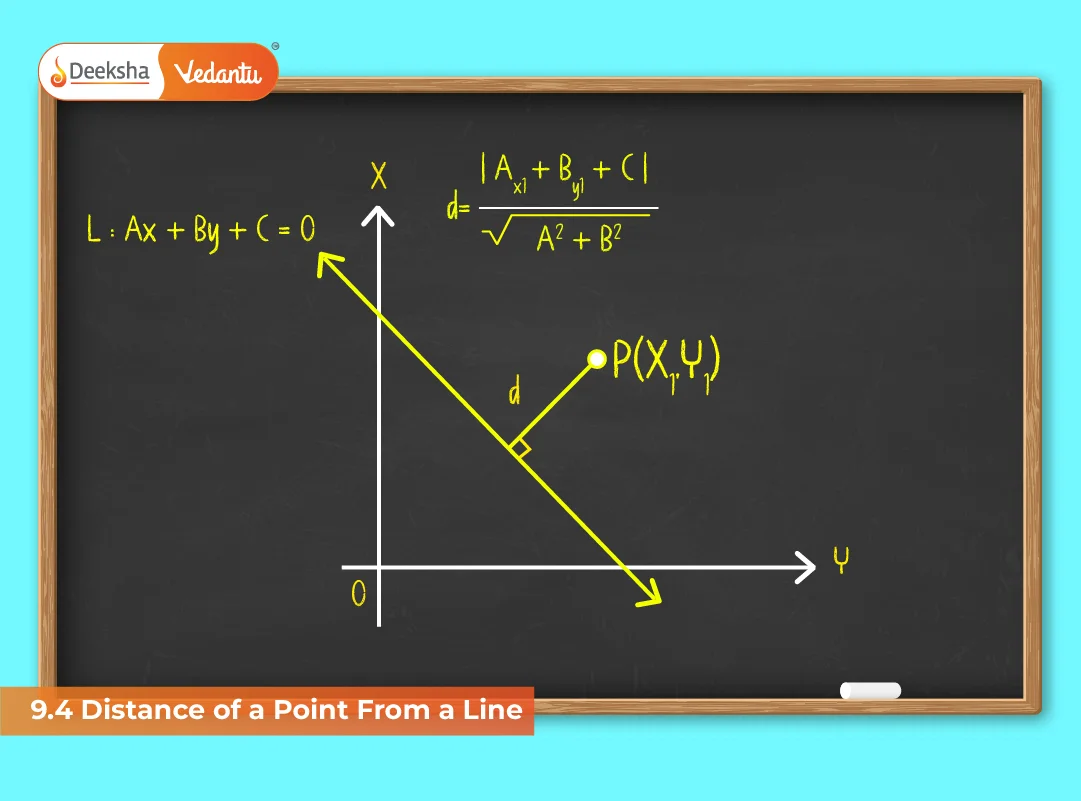
General Formula

If a line is given in the general form:

ax + by + c = 0

and a point P(x₁, y₁) is given, the perpendicular distance (d) from P to the line is:

d = |ax₁ + by₁ + c| / √(a² + b²)

This is the most important formula in this section and is directly tested in Boards, JEE, and KCET exams.

Derivation of the Formula

Let the line be ax + by + c = 0 and point P(x₁, y₁).

1. Equation of line in slope form:
   If b ≠ 0 → y = (–a/b)x – c/b.
2. Slope of given line = –a/b.
   Slope of perpendicular from P = b/a.
3. Equation of perpendicular line through P(x₁, y₁):
   y – y₁ = (b/a)(x – x₁).
4. Solve this with a given line equation to get the foot of perpendicular Q.
5. Distance between P(x₁, y₁) and Q(x₂, y₂) = √((x₂ – x₁)² + (y₂ – y₁)²).

On simplifying → formula:
d = |ax₁ + by₁ + c| / √(a² + b²)

Special Cases

1. If P lies on line ax + by + c = 0, then ax₁ + by₁ + c = 0, hence d = 0.
2. If line is vertical (x = k), then distance of P(x₁, y₁) = |x₁ – k|.
3. If line is horizontal (y = k), then distance of P(x₁, y₁) = |y₁ – k|.

Solved Examples

Example 1
Find distance of point (3, 4) from line 3x – 4y + 5 = 0.

d = |3(3) – 4(4) + 5| / √(9 + 16) = |9 – 16 + 5| / 5 = |–2| / 5 = 2/5.

Example 2
Find distance of (–2, –1) from line x + 2y + 3 = 0.

d = |(–2) + 2(–1) + 3| / √(1² + 2²) = |–2 – 2 + 3| / √5 = |–1| / √5 = 1/√5.

Example 3
Find distance of point (1, –2) from line y = 2x + 3.

Rewriting line: 2x – y + 3 = 0.
d = |2(1) – (–2) + 3| / √(2² + (–1)²) = |2 + 2 + 3| / √5 = 7/√5.

Example 4 (Board Type)
Find perpendicular distance of origin (0, 0) from line 5x – 12y + 13 = 0.

d = |0 + 0 + 13| / √(25 + 144) = 13/13 = 1.

Example 5 (JEE Style)
Find k if the distance of (3, –2) from line kx – 4y + 5 = 0 is 5.

Formula: d = |3k – 4(–2) + 5| / √(k² + 16) = 5
→ |3k + 13| = 5√(k² + 16).
Square both sides, solve for k.

Example 6 (KCET Style)
Find distance of point (7, 2) from line joining (3, –1) and (–2, 4).

Equation of line through (3, –1) and (–2, 4):
(y + 1)/(4 + 1) = (x – 3)/(–2 – 3) → (y + 1)/5 = (x – 3)/(–5).
Simplify: x + y – 2 = 0.

Distance d = |7 + 2 – 2| / √2 = 7/√2.

Applications in Geometry

1. Equation of parallel lines at a fixed distance:
   Given line ax + by + c = 0, parallel lines at distance d are ax + by + c ± d√(a² + b²) = 0.
2. Finding locus:
   If the distance of point (x, y) from a line is constant, the locus forms another line parallel to it.
3. Shortest distance problems:
   In optimization, the distance formula minimizes/maximizes paths.

Common Mistakes

1. Forgetting to take absolute value in numerator.
2. Using formula without ensuring line is in ax + by + c = 0 form.
3. Confusing shortest distance with direct distance between two arbitrary points.
4. Forgetting to normalize coefficients (important in normal form).

Exam Weightage

CBSE Boards: 2–3 marks for direct formula application, sometimes 4 marks if linked with locus.
JEE Main: 1 question frequently, either direct distance or condition on k for given distance.
KCET/COMEDK: 1–2 MCQs.
JEE Advanced: Used in locus problems, optimization, and family of lines.

Practice Problems

1. Find distance of (4, –3) from line 2x + y – 5 = 0.
2. Find distance of (–2, 1) from line 4x – 3y + 6 = 0.
3. Find distance between parallel lines 3x – 4y + 7 = 0 and 3x – 4y – 5 = 0.
4. Find k if the distance of (2, 3) from line 3x + 4y – k = 0 is 5.
5. Show that distance of (x₁, y₁) from line ax + by + c = 0 is zero if point lies on the line.
6. Find distance of (–1, –1) from line joining (0, 2) and (2, 0).
7. Find equations of two lines parallel to 2x + y – 5 = 0 at distance 3 units.
8. Find distance of origin from line 7x – 24y + 25 = 0.
9. A variable line moves such that its perpendicular distance from origin is 4. Find its equation.
10. Find k if the distance between lines x + y – k = 0 and x + y + 2 = 0 is √2.

FAQs

Q1. What is the distance of a point from a line?
It is the length of the perpendicular dropped from the point onto the line.

Q2. Why is absolute value taken in formula?
Because distance is always non-negative.

Q3. What if the point lies on line?
Then distance = 0.

Q4. How to find distance between two parallel lines?
If equations are ax + by + c₁ = 0 and ax + by + c₂ = 0, distance = |c₁ – c₂|/√(a² + b²).

Q5. How often does this appear in JEE/KCET?
Almost every year, usually as part of geometry or locus problems.